“These types of dense suspensions are found everywhere,” said Ivan Christov, assistant professor of mechanical engineering. “It can be anything from the fluids in your body, to ingredients mixed in your kitchen, to industrial slurries. Even mud on the ground is a fluid – a bunch of irregularly-shaped dirt particles densely suspended in water.”

The interactions between fluid mechanics and particle science make it very difficult to model these dense suspensions.  “The particles’ movements are influenced by the fluid, and the fluid’s motion is influenced by the particles,” said Christov. “It’s an unavoidable coupling. And because it’s not a homogenous substance, the density keeps changing, which also changes the flow behavior. We can’t use the regular equations of fluid mechanics, and it’s not possible to computationally keep track of millions of individual particles.”

The solution is to treat those particles as if they were a separate, hypothetical “fluid.” Then, by utilizing models of how two fluids interact, the flow of these dense suspensions can be accurately modeled in the computer.  Christov’s work on this two-fluid model has been published in the International Journal of Multiphase Flow.

While two-fluid models have been theorized for years, Christov and his team at the Transport: Modeling, Numerics & Theory Laboratory had a lot of mathematics to tackle in order to create a working model.  They validated the model by comparing their results to two previous real-world experiments. One involved a cylinder rotating inside another cylinder, mixing two fluids together. Another occurred at the microscale, with a fluid microchannel the width of a human hair. A herringbone-shaped cutout in the channel interrupts the flow, mixing the two fluids in a specific pattern. In both cases, Christov’s computer models showed the same results as the real-world experiments.

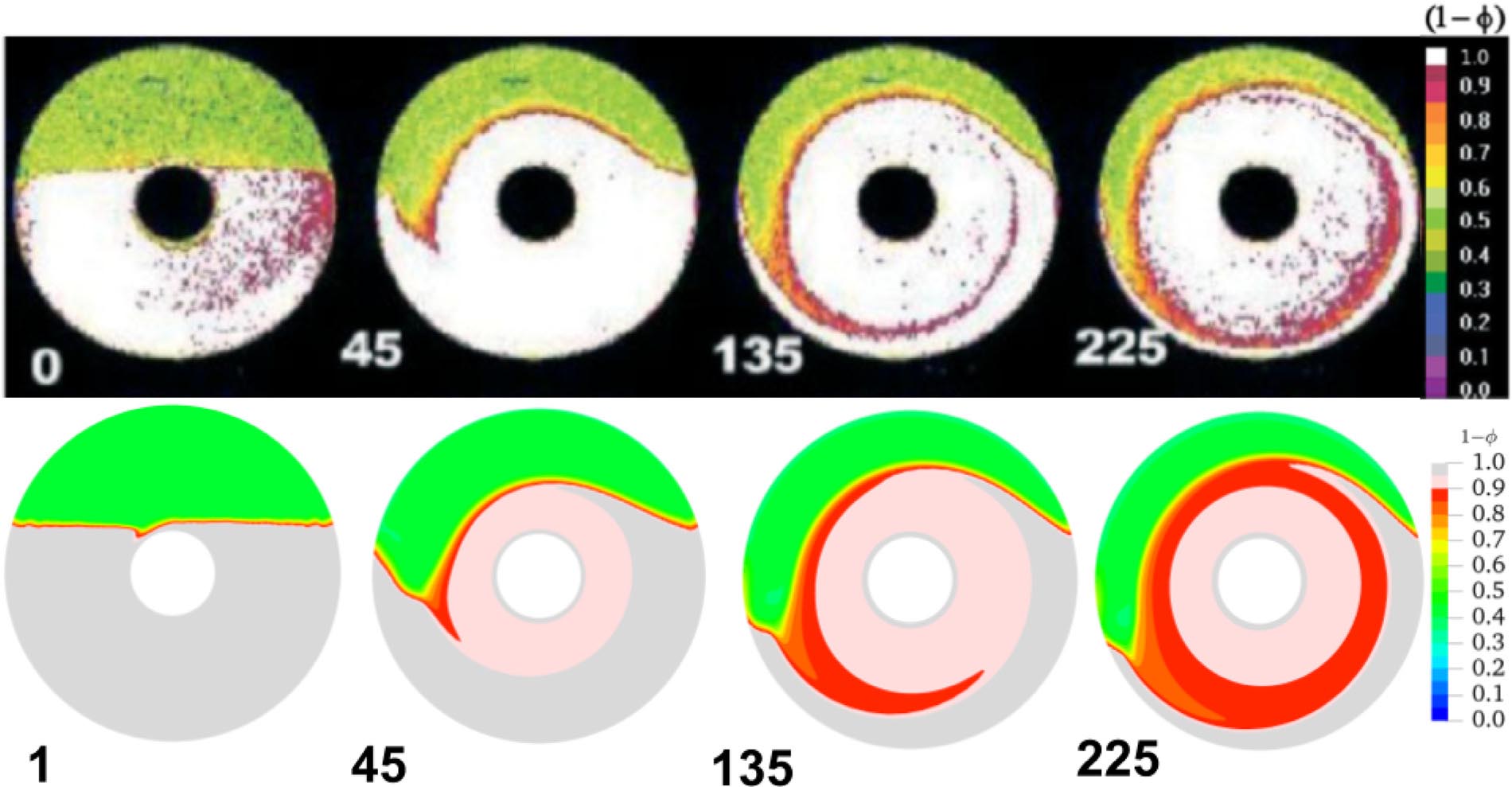Christov's simulated results (bottom) compared with a real-world fluid suspension experiment

“So we have validations of both macroscale and microscale experiments,” said Christov. “This means that it can be used as a general computational tool to predict the flow behavior of dense suspensions in many different regimes, in both simple and complicated geometries.”

Christov’s team performed their calculations with the help of Purdue’s Rosen Center for Advanced Computing. They made use of open source tools like the computation fluid dynamics platform OpenFOAM, and have published their implementation as open-source code on GitHub, making it available to anyone. 

As for the future, Christov has seen his models put to work in various ways: from the behavior of cells in low-gravity conditions, to the slurry used in fracking (the initial research was funded by the American Chemical Society Petroleum Research Fund). His team is also collaborating with heat transfer professor Amy Marconnet, to investigate whether the movement of these dense suspensions can be used to cool microchips.

“From a modeling point of view, you’re always excited when you put in the right equations and everything matches,” said Christov. “We look forward to seeing how this model will be used in the future.”

Writer: Jared Pike, jaredpike@purdue.edu, 765-496-0374

Source: Ivan Christov, christov@purdue.edu, 765-496-3733

A two-fluid model for numerical simulation of shear-dominated suspension flows

Federico Municchi, Pranay P. Nagrani, Ivan C. Christov

https://doi.org/10.1016/j.ijmultiphaseflow.2019.07.015

ABSTRACT: Suspension flows are ubiquitous in nature (hemodynamics, subsurface fluid mechanics, etc.) and industrial applications (hydraulic fracturing, CO2 storage, etc.). However, such flows are notoriously difficult to model due to the variety of fluid-particle and particle-particle interactions that can occur. In this work, we focus on non-Brownian shear-dominated suspensions, where kinetic collisions are negligible and frictional effects play a dominant role. Under these circumstances, irreversible phenomena such as particle diffusion and migration arise, requiring anisotropic stress models to describe the suspension rheology. On a continuum level, reduced-order models such as the suspension balance model (SBM) or the diffusive flux model are commonly used to predict particle migration phenomena. We propose a new method based on a two-fluid model (TFM), where both the phases are considered as interpenetrating continua with their own conservation of mass and momentum equations. Without employing the nowadays customary simplifications in applying the SBM, we close the “full” TFM instead. Specifically, we show that when an anisotropic stress analogous to that used in the SBM is added to the equilibrium equations for the particle phase, the TFM is able to accurately predict particle migration. Thus, the TFM does not require the assumptions of a steady suspension velocity and a Stokesian (inertialess) fluid, and the TFM can be easily extended to include buoyancy and even kinetic collisional models. We present several benchmark simulations of our TFM implementation in OpenFOAM®, including in curvilinear coordinates and three- dimensional flow. Good agreement between the TFM solutions and previous experimental and numerical results is found.