Image denoising aims at reconstructing a clean image from the noisy measurement. The figure shows a simulated noisy image and the recovery using a deep neural network.

When training a deep neural network for image processing tasks such as image denoising, it has long been observed that the network can only perform well at the noise level where it is trained for. Purdue researchers recently developed a new theoretical framework which allows the network to handle a wide range noise levels where the performance is guaranteed to have a uniform gap from their individual best.

“Traditionally, when people train one deep neural network for a range of noise levels, they allocate training samples uniformly across the noise range” said Abhiram Gnanasambandam, a PhD student of Prof. Stanley Chan, assistant professor of ECE and Statistics. “This unbiased sampling is simple and very popular. However, since difficult cases contribute more to the overall risk, the network has a tendency to favor them more than the easy cases. So you will see a large gap from what it produces compared to what it can best perform at the low noise cases, but a very small gap at the high noise cases.”

He says this can be undesirable for many computational imaging applications where the gap needs be consistent throughout the noise range.

The solution Gnanasambandam and Prof. Chan developed is to re-allocate the training samples. The idea is to re-formulate the learning problem as a minimax optimization. Instead of just trying to minimize the usual empirical risk, they introduce a constraint such that the worst case is bounded. What is more surprising is that while the problem appears difficult because deep neural networks are generally nonlinear, the minimax problem has a dual which is always convex. In addition, the dual formulation can lead to a very efficient algorithm that adjusts the training distribution while training the network. The algorithm is guaranteed to converge to a global minimum or a convex relaxation solution.

A new theoretical framework is developed to train a single deep neural network for a wide range of noise levels such that the performance has a consistent gap from the ideal case. Conventional (uniform) distribution typically demonstrates worse performance at low-noise situations which can be undesirable. Figure courtesy: Stanley Chan

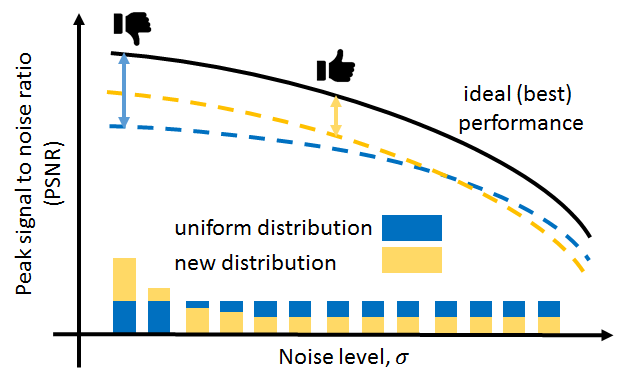
“This is a beautiful result,” said Prof. Chan. “It applies to all networks because the theory does not depend on a particular network architecture. All we do is to change the training sample distribution, and we can offer theoretical guarantees. The approach also appears to be generalizable to other imaging tasks such as image super-resolution, deblurring, compressed sensing, and tomography. So it is exciting to see simplicity, effectiveness, theoretical guarantee and generality, all at once.”

The work will be presented in the 37^th International Conference on Machine Learning (ICML), Vienna Austria, July 2020 (virtual conference due to COVID 19). ICML is one of the flagship conferences of machine learning research. The typical acceptance rate is 20%.

Reference:

Abhiram Gnansambandam and Stanley H. Chan, ‘‘One size fits all: Can we train one denoiser for all noise levels?’’, Journal of Machine Learning Research Workshop and Conference Proceedings (ICML), 2020. Manuscript of this paper is available online at https://arxiv.org/abs/2005.09627