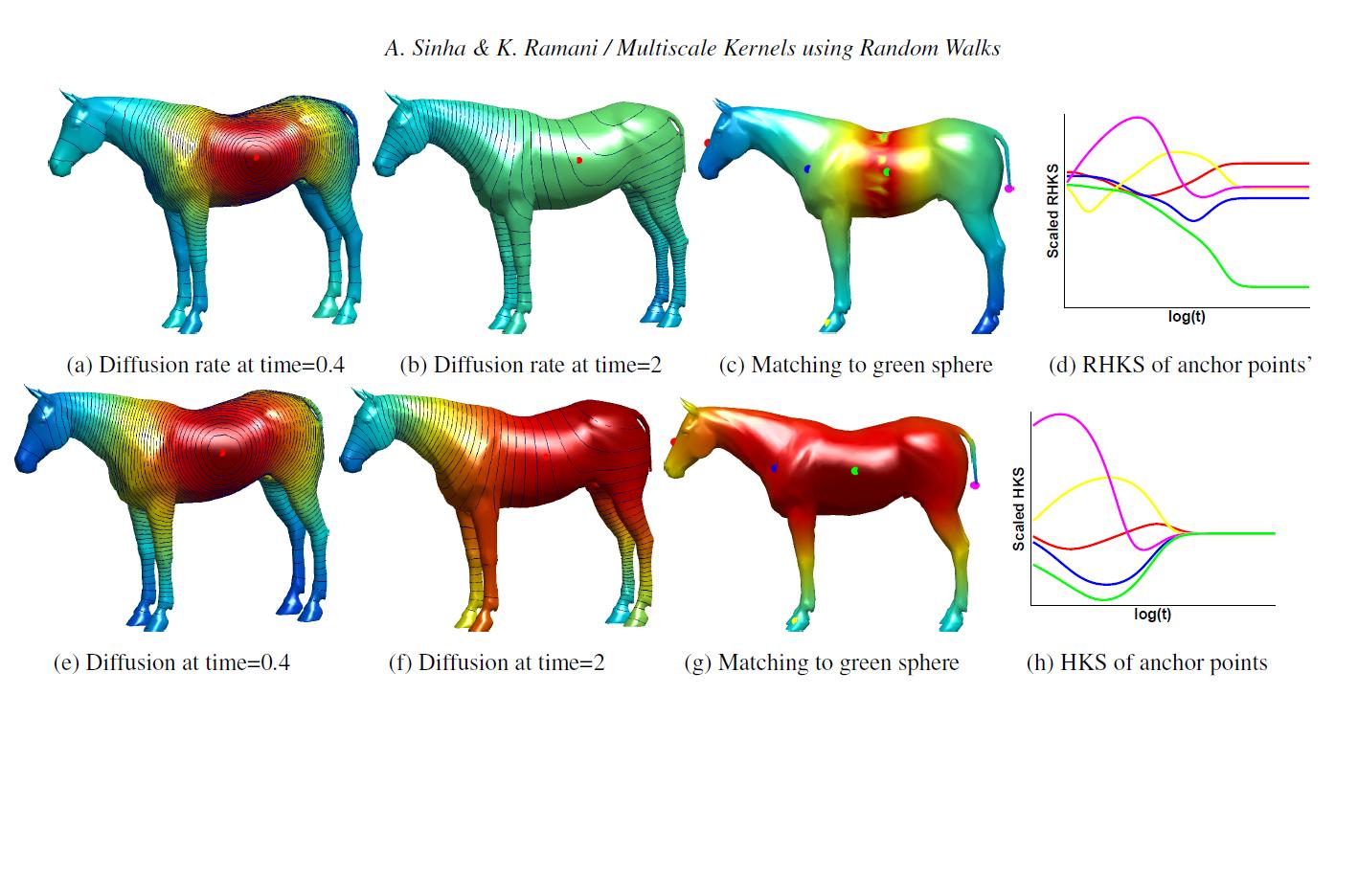
Multiscale Kernels using Random Walks

by | Jul 10, 2013

Authors: Karthik Ramani, Ayan Sinha
11th Symposium on Geometry processing, 3-5 July, Genova, Italy, 2013. Proceedings of the Computer Graphics Forum, Computer Graphics Forum, Volume 33, Issue 1, pages 164–177, 2014.
Paper

ABSTRACT
We introduce novel multiscale kernels using the random walk framework and derive corresponding embeddings and pairwise distances. The fractional moments of the rate of continuous time random walk (equivalently diffusion rate) are used to discover higher order kernels (or similarities) between pair of points. The formulated kernels are isometry, scale, and tessellation invariant, can be made globally or locally shape aware, and are insensitive to
partial objects and noise based on the moment and influence parameters. Additionally, the corresponding kernel distances and embeddings are convergent and efficiently computable. We introduce dual GMS signatures based
on the kernels and discuss the applicability of the multiscale distance and embedding. Collectively, we present a unified view of popular embeddings and distance metrics while recovering intuitive probabilistic interpretations
on discrete surface meshes.

 

Categories and Subject Descriptors (according to ACM CCS): I.3.5 [Computer Graphics]: Computational Geometry and Object Modeling—Geometric algorithms, languages, and systems

 

ayan

ayan

Ayan is a PhD student in the School of Mechanical Engineering, Purdue University, since Fall 2011. He completed his undergraduate studies (B.Tech) from I.I.T., Kharagpur (Spring 2009) and subsequently received his masters (M.S.) from Georgia Tech (Spring 2011), all in mechanical engineering. His current work focuses on using random walks and spectral graph theory for understanding the multiscale structure and evolution of graphs over time. The applications include 3D shape analysis, retrieval, correspondence for geometric graphs (or manifolds) and clustering, evaluation, hierarchical community structure finding for social network graphs.