Image Denoising and Restoration
Fast and Robust Recursive Filters
 |
Image denoising on mobile cameras requires low complexity, but many
state-of-the-art denoising methods are computationally intensive. We present
a low complexity denoising algorithm using an edge-aware recursive filter
(RF). We make two contributions. First, we modify the original RF so that it
is significantly more robust when estimating the gradients from noisy inputs.
We extend the RF to high-order for texture and heavy noise images. Second, we
introduce a SURE-based image fusion technique. We show that while individual
RFs have different performance, the fused result is often better.
Experimental results show that the new RF performs much faster than other
denoisers while providing good quality images. MATLAB Implementation (1.2MB) Publication:
|
Symmetric Smoothing Filters
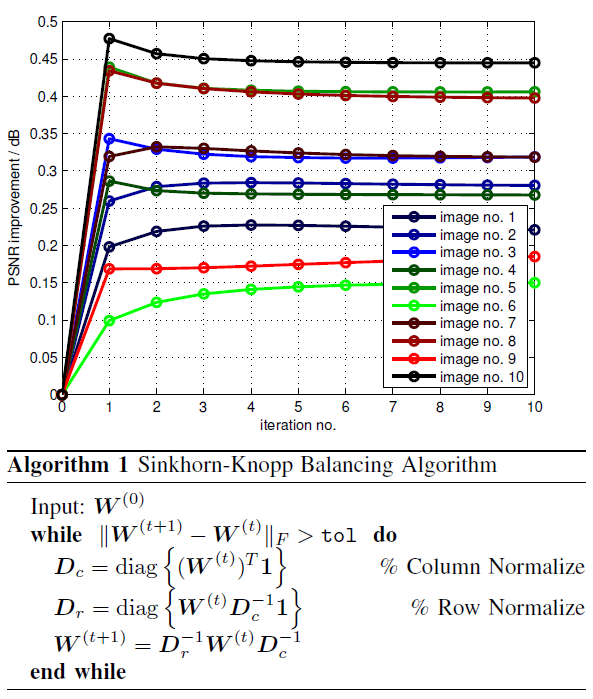 |
We study a class of smoothing filters for image denoising. Expressed as matrices, these smoothing filters must be row
normalized so that each row sums to unity. Surprisingly, if one applies a column normalization to the matrix before the
row normalization, the denoising quality can often be significantly improved. This column-row normalization corresponds
to one iteration of a symmetrization process called the Sinkhorn-Knopp balancing algorithm. However, a complete
understanding of the performance gain phenomenon is lacking. Our Contribution: We analyze the performance gain from a Gaussian mixture model (GMM) perspective. We show that the
symmetrization is equivalent to an expectation-maximization (EM) algorithm for learning the GMM. Moreover, we make
modifications to the symmetrization procedure and present a new denoising algorithm. Experimental results show that the
new algorithm achieves comparable denoising results to some state-of-the-art methods. Publication:
|
Monte-Carlo Non-local Means
 |
Non-local means (Buades et al 2005) is a simple yet effective image denoising algorithm. More strikingly, Levin and
Nadler (2012) showed that non-local means are indeed the optimal denoising algorithm in the mean squared sense when
we have an infinitely large database of clean patches. While these results are beautiful, in reality such computation
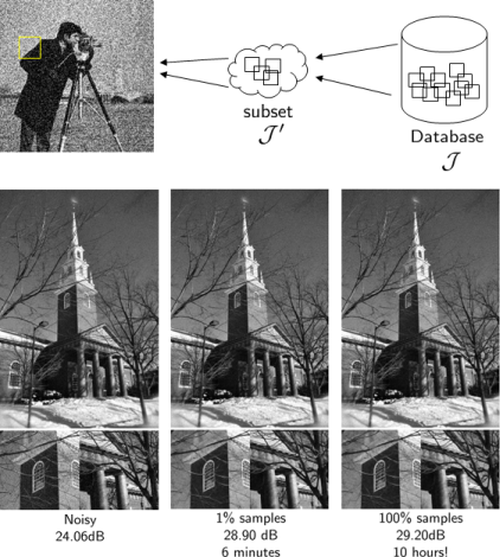
are very difficult due to its scale. MCNLM is the first practical solution towards this problem. Our contributions: We show that only a small subset of patches are sufficient to produce the denoising result. We provide rigorous
proofs using probabilistic large-deviation theory. We derive optimal sampling schemes and implemented a method for the denoising problem. We demonstrate orders of magnitude in speed up
with minimal degradation in quality. Publication:
|
Image Denoising by Prior Adaptation
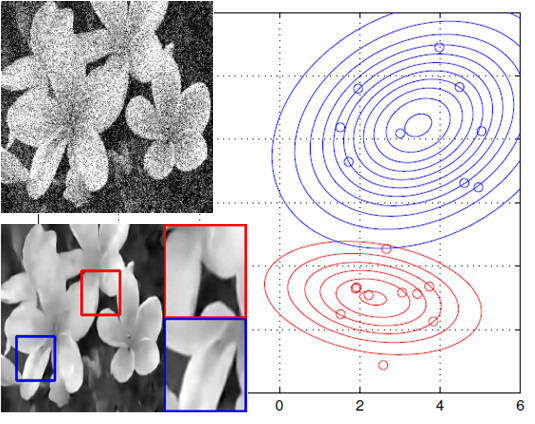 |
Effective image prior is a key factor for successful image denoising. Existing learning-based priors require a large
collection of images for training. Besides being computationally expensive, these training images do not necessarily
correspond to the noisy image of interest. Our Contribution: We propose an adaptive learning procedure for learning image patch priors. The new algorithm, called
the Expectation-Maximization (EM) adaptation, maps a generic prior to a targeted image to create a specific prior. EM
adaptation requires significantly less amount of training data compared to the standard EM, and can be applied to
pre-filtered images in the absence of clean databases. Experimental results show that the adapted prior is consistently
better than the originally un-adapted prior, and has superior performance than some state-of-the-art algorithms. Publication:
|
Image Denoising by Targeted External Databases
 |
Human uses prior knowledge to analyze an image; So is our desire to put on a computer. However, the priors we use to
train the computers today are perhaps too generic. In many image denoising methods, the priors are learned from a large
collection of natural images comprising of a huge diversity of scenes. Of course, in the asymptotic limit such kind of
priors will work. Yet for a particular image denoising task with only limited computing budget this can be far from
optimal. To address this problem we propose to study the optimal denoising algorithm using a specific (or targeted)
database. For example, if we want to denoise a text document, then we shall use priors of the text. Surprisingly, this
simple idea is sufficient to outperform some of the state-of-the-art denoising algorithms. Publication:
|
Total Variation Minimization
 |
In this project, we develop a fast numerical optimization method to solve total variation image restoration problems. The method transforms the original
unconstrained problem to an equivalent constrained problem and uses an augmented Lagrangian method to handle the constraints. The transformation allows
the differentiable and non-differentiable parts of the objective function to be separated into different subproblems where each subproblem may be solved
efficiently. An alternating strategy is then used to combine the subproblem solutions. Publication:
|
Depth Estimation: Reconstruction and Sampling
 |
Acquiring depth information is the first and the most important step for 3D image processing. Existing depth
acquisition methods either use expensive hardware devices and computationally intensive block matching algorithms. We
propose a compressive sensing based method to estimate the depth using a few samples. Our solution is unique in
the following sense:
Publication:
|
Motion Estimation
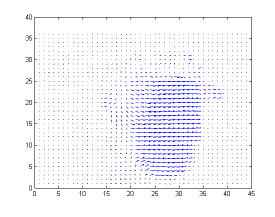 |
In conventional block matching motion estimation algorithms, subpixel motion accuracy is achieved by searching the best matching block in an enlarged
(interpolated) reference search area. This, however, is computationally expensive as the number of operations required is directly proportional to the
interpolation factor. For non video compression based applications, the interpolation process is even wasteful as the motion compensation frames are not
needed. This project aims at developing a fast motion estimation algorithm that achieves subpixel accuracy without interpolation. We show that by fusing
the existing integer block matching algorithm and a modified optical flow method, subpixel motion vectors can be determined at the cost of integer block
matching plus solving a 2-by-2 systems of linear equations. Experimental results demonstrate that the proposed method is faster than conventional method
by a factor of 2 (or more), while the motion vector quality is compatible to the benchmark full search algorithm. Publication:
|