Intelligent Imaging Lab
Robust Machine Learning
Selected Publications
Why Fine-grained Labels in Pretraining Benefit Generalization?
Guan Zhe Hong, Yin Cui, Ariel Fuxman, Stanley H. Chan, Enming Luo
Transactions on Machine Learning Research, 2024
Optical Adversarial Attack
Abhiram Gnanasambandam, Alex M. Sherman, and Stanley H. Chan
IEEE ICCV Workshop, 2021
Media Coverage:
Detecting and Segmenting Adversarial Graphics Patterns from Images
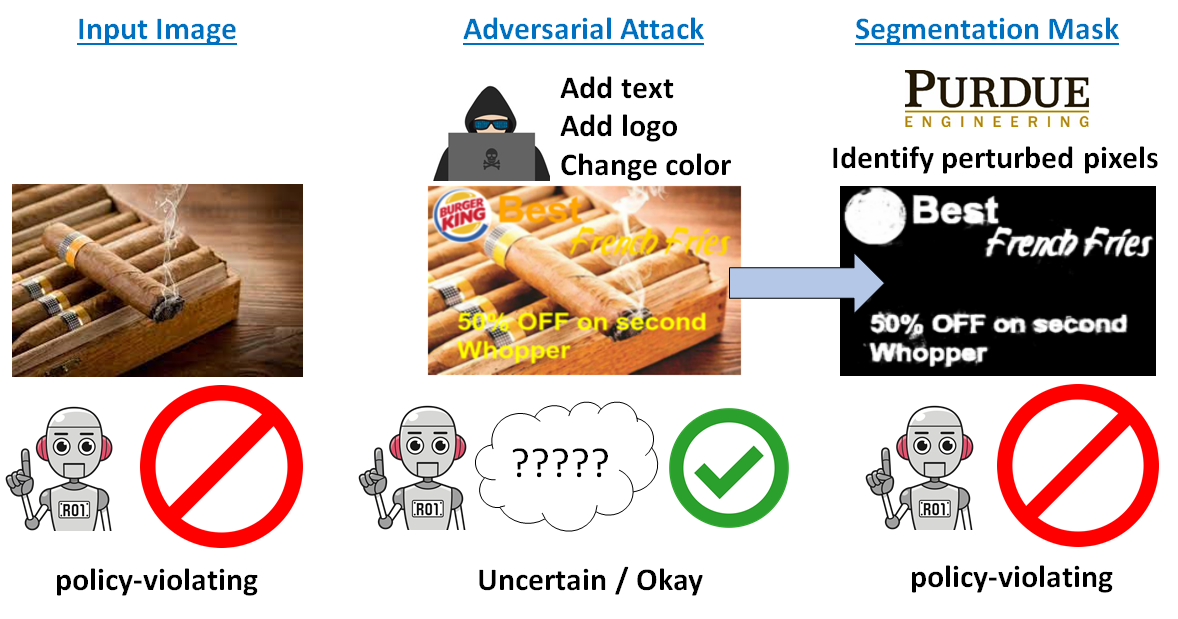
Xiangyu Qu and Stanley H. Chan
IEEE ICCV Workshop, 2021
Student-Teacher Learning from Clean Inputs to Noisy Inputs
Guanzhe Hong, Zhiyuan Mao, Xiaojun Lin, and Stanley H. Chan
IEEE CVPR, 2021
One Size Fits All: Can We Train One Denoiser for All Noise Levels?
Abhiram Gnansambandam and Stanley H. Chan
ICML, 2020
ConsensusNet: Optimal Combination of Image Denoisers
Joon Hee Choi, Omar A. Elgendy and Stanley H. Chan
IEEE Transactions on Image Processing, 2019