Plug and Play ADMM

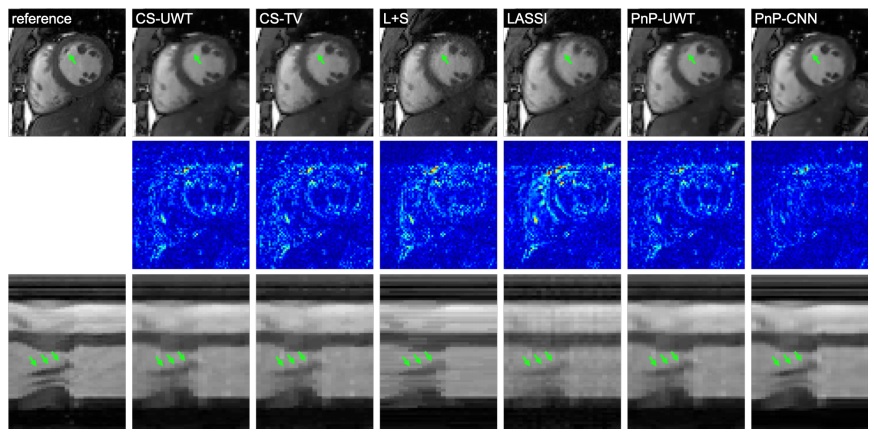Magnetic Resonance Imaging (MRI) is a non-invasive diagnostic tool that provides excellent soft-tissue contrast without the use of ionizing radiation. Compared to other clinical imaging modalities (e.g., CT or ultrasound), however, the data acquisition process for MRI is inherently slow, which motivates undersampling and thus drives the need for accurate, efficient reconstruction methods from undersampled datasets. In this article, we describe the use of “plug-and-play” (PnP) algorithms for MRI image recovery. We first describe the linearly approximated inverse problem encountered in MRI. Then we review several PnP methods, where the unifying commonality is to iteratively call a denoising subroutine as one step of a larger optimization-inspired algorithm. Next, we describe how the result of the PnP method can be interpreted as a solution to an equilibrium equation, allowing convergence analysis from the equilibrium perspective. Finally, we present illustrative examples of PnP methods applied to MRI image recovery.

Publication:

Rizwan Ahmad, Charles A. Bouman, Gregery T. Buzzard, Stanley H. Chan, Edward T. Reehorst, Philip Schniter, ‘‘Plug-and-Play methods for magnetic resonance imaging’’, IEEE Signal Processing Magazine, 2019.

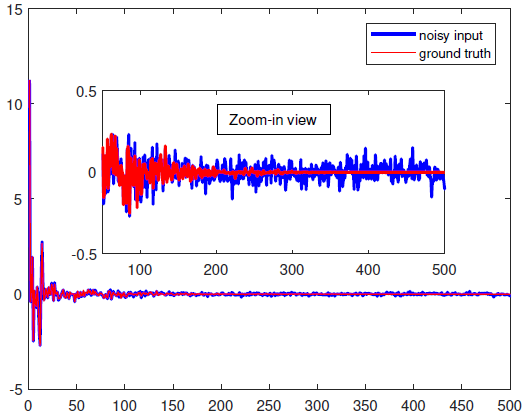The Plug-and-Play (PnP) ADMM algorithm is a powerful image restoration framework that allows advanced image denoising priors to be integrated into physical forward models to yield a provably convergent algorithm. However, despite the enormous applications and promising results, very little is known about why the PnP ADMM performs so well. This paper presents a formal analysis of the performance of PnP ADMM. By restricting the denoisers to the class of graph filters, or more specifically the symmetric smoothing filters, we offer three contributions: (1) We rigorously show conditions under which an equivalent maximum-a-posteriori (MAP) optimization exists, (2) we derive the mean squared error of the PnP solution, and provide a simple geometric interpretation which can explain the performance, (3) we introduce a new analysis technique via the concept of consensus equilibrium, and provide interpretations to general linear inverse problems and problems with multiple priors.

Publication:

Stanley H. Chan, ‘‘Performance analysis of Plug-and-Play ADMM: A graph signal processing perspective’’, IEEE Trans. Comp. Imaging, vol. 5, no. 2, pp. 274-286, Jun. 2019.

Regularized inversion methods for image reconstruction are used widely due to their tractability and ability to combine complex physical sensor models with useful regularity criteria. Such methods motivated the recently developed Plug-and-Play prior method, which provides a framework to use advanced denoising algorithms as regularizers in inversion. However, the need to formulate regularized inversion as the solution to an optimization problem limits the possible regularity conditions and physical sensor models. In this paper, we introduce Consensus Equilibrium (CE), which generalizes regularized inversion to include a much wider variety of both forward components and prior components without the need for either to be expressed with a cost function. CE is based on the solution of a set of equilibrium equations that balance data fit and regularity. In this framework, the problem of MAP estimation in regularized inversion is replaced by the problem of solving these equilibrium equations, which can be approached in multiple ways. The key contribution of CE is to provide a novel framework for fusing multiple heterogeneous models of physical sensors or models learned from data. We describe the derivation of the CE equations and prove that the solution of the CE equations generalizes the standard MAP estimate under appropriate circumstances. We also discuss algorithms for solving the CE equations, including ADMM with a novel form of preconditioning and Newton's method. We give examples to illustrate consensus equilibrium and the convergence properties of these algorithms and demonstrate this method on some toy problems and on a denoising example in which we use an array of convolutional neural network denoisers, none of which is tuned to match the noise level in a noisy image but which in consensus can achieve a better result than any of them individually.

MATLAB Implementation

Publication:

Gregery T. Buzzard, Stanley H. Chan, Suhas Sreehari and Charles A. Bouman ‘‘Plug-and-Play unplugged: Optimization free reconstruction using consensus equilibrium’’, SIAM Journal on Imaging Science, vol. 11, no. 3, pp.2001-2020, Sep. 2018.

While foreground extraction is fundamental to virtual reality systems and has been studied for decades, majority of the professional softwares today still rely substantially on human interventions, e.g., providing trimaps or labeling key frames. This is not only time consuming, but is also sensitive to human error. In this paper, we present a fully automatic foreground extraction algorithm which does not require any trimap or scribble. Our solution is based on a newly developed concept called the Multi-Agent Consensus Equilibrium (MACE), a framework which allows us to integrate multiple sources of expertise to produce an overall superior result. The MACE framework consists of three agents: (1) A new dual layer closed-form matting agent to estimate the foreground mask using the color image and a background image; (2) A background probability estimator using color difference and object segmentation; (3) A total variation minimization agent to control the smoothness of the foreground masks. We show how these agents are constructed, and how their interactions lead to better performance. We evaluate the performance of the proposed algorithm by comparing to several state-of-the-art methods. On the real datasets we tested, our results show less error compared to the other methods.

Publication:

1. Xiran Wang, Jason Juang, Stanley H. Chan, ‘‘Automatic Foreground Extraction using Multi-Agent Consensus Equilibrium’’.

Signals defined on a network or a graph are often prone to errors due to missing data and noise. In order to restore the graph signal, interpolation and denoising are two necessary steps along with other graph signal processing procedures. However, existing graph signal interpolation and denoising methods are largely decoupled due to the opposite objectives of the two tasks and the inherent high computational complexity. The goal of this paper is to integrate graph interpolation and denoising using the Plug-and-Play (PnP) ADMM, a recently developed technique in image processing. When using the subsampling process as the forward model and graph filter as the denoiser, we show that PnP ADMM is equivalent to interpolating a bandlimited signal. Preliminary results are demonstrated via experiments, where the proposed method shows significantly better performance over existing methods.

Publication:

Yoshinao Yazaki, Yuichi Tanaka, and Stanley H. Chan, ‘‘Interpolation and denoising of graph signals using Plug-and-Play ADMM’’, IEEE ICASSP, pp. 5431-5435, Brighton, United Kingdom, May 2019.

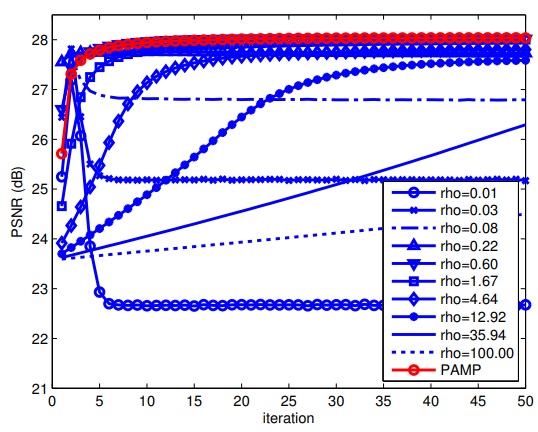Plug-and-Play ADMM is a recently developed variation of the classical ADMM algorithm that replaces one of the subproblems using an off-the-shelf image denoiser. Despite its apparently ad-hoc nature, Plug-and-Play ADMM produces surprisingly good image recovery results. However, since in Plug-and-Play ADMM the denoiser is treated as a black-box, behavior of the overall algorithm is largely unknown. In particular, the internal parameter that controls the rate of convergence of the algorithm has to be adjusted by the user, and a bad choice of the parameter can lead to severe degradation of the result. In this paper, we present a parameter-free Plug-and-Play ADMM where internal parameters are updated as part of the optimization. Our algorithm is derived from the generalized approximate message passing, with several essential modifications. Experimentally, we find that the new algorithm produces solutions along a reliable and fast converging path.

Publication:

1. Xiran Wang and Stanley H. Chan, ‘‘Parameter-free Plug-and-Play ADMM for image restoration’’, IEEE ICASSP, pp.1323-1327, New Orleans, Louisiana, Mar. 2017.
   

We propose a Plug-and-Play ADMM algorithm with provable fixed point convergence. We show that for any denoising algorithm satisfying an asymptotic criteria, called bounded denoisers, Plug-and-Play ADMM converges to a fixed point under a continuation scheme. We also present fast implementations for two image restoration problems on super-resolution and single-photon imaging. We compare Plug-and-Play ADMM with state-of-the-art algorithms in each problem type, and demonstrate promising experimental results of the algorithm.

MATLAB Implementation

Publication:

1. Stanley H. Chan, Xiran Wang, and Omar Elgendy, ‘‘Plug-and-Play ADMM for image restoration: Fixed point convergence and applications’’, IEEE Trans. Comp. Imaging, vol. 3, no. 5, pp.84–98, Mar. 2017.