Imaging through Atmospheric Turbulence

Overview

Imaging through atmospheric turbulence is a fundamental problem for long-range imaging systems. Purdue i2Lab has specialities in several aspects of the subject:

Wave optics theory
Turbulence simulators
Forward imaging models that can be used for deep neural networks
Image reconstruction algorithms
Object recognition

Book

Stanley H. Chan and Nicholas Chimitt, Computational Imaging through Atmospheric Turbulence, Now Publisher 2023.

Tutorial

ICIP 2022 and CVPR 2022
Instructors: Stanley Chan and Nick Chimitt

Recordings

Purdue Atmospheric Turbulence Simulator

Phase-over-aperture model (Version 1)

Key Concept: Collapse screens and sample in the Zernike space. 20x speed up compared to split-step.

Publication:

Nicholas Chimitt and Stanley H. Chan, ‘‘Simulating Anisoplanatic Turbulence by Sampling Correlated Zernike Coefficients’’, Optical Engineering, 59(8), 083101, July 2020. (A shorter version is presented in IEEE ICCP 2020.)

Code:

MATLAB download: (URL)

Project Page: https://github.itap.purdue.edu/StanleyChanGroup/TurbulenceSim_v1Public

Licence: Copyright is granted for educational and research purposes. Please contact Prof Chan for licensing.

Phase-to-space transform (Version 2)

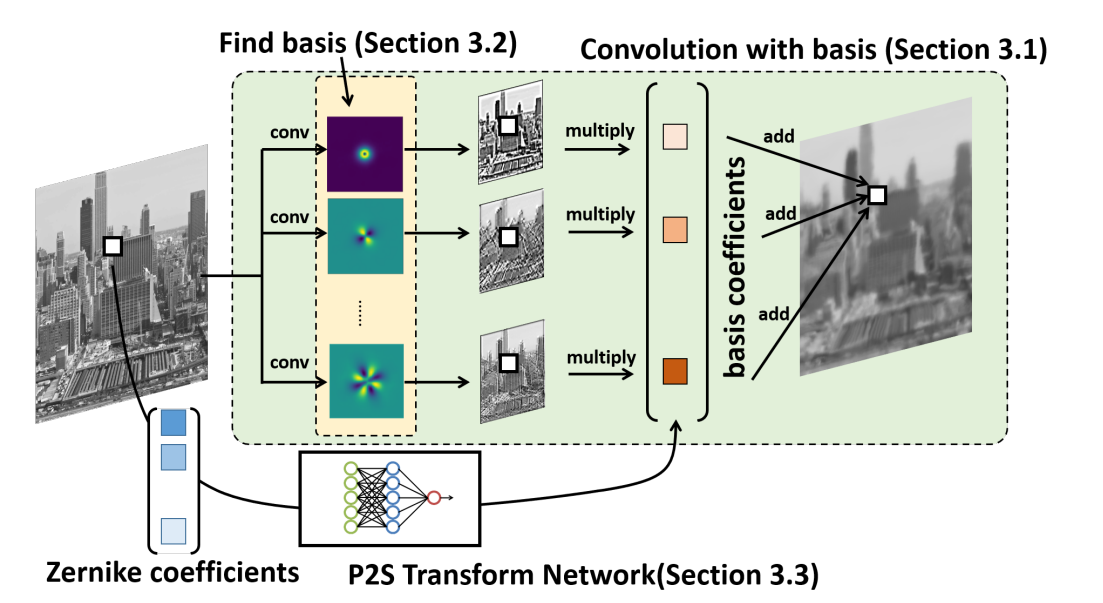Key Concept: Transform Zernike representation to PSF representation. 1000x speed up compared to split-step.

Publication:

Zhiyuan Mao, Nicholas Chimitt and Stanley H. Chan, ‘‘Accelerating Atmospheric Turbulence Simulation via Learned Phase-to-Space Transform’’, accepted to IEEE International Conference on Computer Vision, 2021.

Project Page: https://github.itap.purdue.edu/StanleyChanGroup/TurbulenceSim_P2S

Licence: Copyright is granted for educational and research purposes. Please contact Prof Chan for licensing.

Dense field phase-to-space transform (Version 3)

Key concept: Quantize and decouple Zernike mode and spatial mode to preserve wide sense stationarity. Enables full HD without interpolation.

Publication:

Nicholas Chimitt, Xingguang Zhang, Zhiyuan Mao, and Stanley H. Chan, ‘‘Real- Time Dense Field Phase-to-Space Simulation of Imaging through Atmospheric Turbulence’’, IEEE Trans. Computational Imaging, vol. 8, pp. 1159-1169, Dec. 2022.

Commercial license only

Turbulence Reconstruction

Classical Optimization-based Approach (2020)

Key concept: Lucky imaging + blind deconvolution

Publication:

Zhiyuan Mao, Nicholas Chimitt, and Stanley H. Chan, ‘‘Image Reconstruction of Static and Dynamic Scenes through Anisoplanatic Turbulence’’, IEEE Transactions on Computational Imaging, vol. 6, pp. 1415-1428, Oct. 2020.

Project Page:
https://github.itap.purdue.edu/StanleyChanGroup/TurbRecon_TCI

TurbNet: Single-frame Turbulence Reconstruction (2022)

Key concept: Re-blur the reconstructed image using a turbulence simulator

Publication:

Zhiyuan Mao, Ajay Jaiswal, Zhangyang Wang, and Stanley H. Chan, ‘‘Single Frame Atmospheric Turbulence Mitigation: A Benchmark Study and A New Physics-Inspired Transformer Model’’, European Conference on Computer Vision ECCV, 2022.

Project Page:

https://github.com/VITA-Group/TurbNet

PiRN: Physics-integrated Restoration Network (2023)

Key concept: Simulator in the loop

Publication:

Ajay Jaiswal, Xingguang Zhang, Stanley H. Chan, Zhangyang Wang, ‘‘Physics-Driven Turbulence Image Restoration with Stochastic Refinement’’, IEEE International Conference on Computer Vision (ICCV), 2023.

Project Page:

https://github.com/VITA-Group/PiRN

Turbulence Mitigation Transformer (2024)

Key concept: Two-stage mitigation, transformer, temporal attention

Publication:

Xingguang Zhang, Zhiyuan Mao, Nicholas Chimitt, and Stanley H. Chan, ‘‘Imaging through the Atmosphere using Turbulence Mitigation Transformer’’, IEEE Transactions on Computational Imaging, 2023. [Project Page]

Project Page:

https://github.com/xg416/TMT

Deep Atmospheric Turbulence Mitigation (DATUM) (2024)

Key concept: Consistent with physical methods, recurrent network, deformable attention, version 5 simulator

Publication:

Xingguang Zhang, Nicholas Chimitt, Yiheng Chi, Zhiyuan Mao, and Stanley H. Chan, ‘‘Spatio-Temporal Turbulence Mitigation: A Translational Perspective’’, CVPR, 2024.

Project Page:

https://xg416.github.io/DATUM/

Theoretical Analysis

Tilt-then-Blur or Blur-then-Tilt

Key conclusion: Tilt + blur is the correct model

Publication:

Stanley H. Chan, ‘‘Tilt-then-Blur or Blur-then-Tilt? Clarifying the Atmospheric Turbulence Model’’, IEEE Signal Processing Letters.

Arbitrary Cn2 Profile (Version 4 Simulator)

Key concept: Integrate Cn2 along the path instead of evaluating individual turbulence segments

Publication:

Nicholas Chimitt and Stanley H. Chan, ‘‘Anisoplanatic Optical Turbulence Simulation for Near-Continuous Profiles without Wave Propagation’’, SPIE Optical Engineering (SPIE OpEng), vol. 62, no. 7, pp. 078103, Jul. 2023.

Commercial license only

Dataset generated by this simulator: https://xg416.github.io/DATUM/

Scattering and Gathering for Spatially Varying Convolutions (Version 5 Simulator)

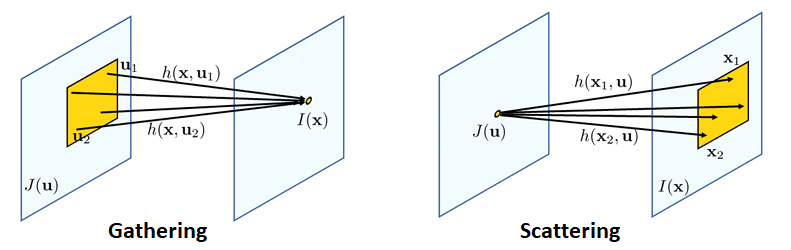Key finding: Scattering is for optics simulation, whereas gathering is for signal filtering

Publication:

Nicholas Chimitt, Xingguang Zhang, Yiheng Chi, Stanley H Chan, ‘‘Scattering and Gathering for Spatially Varying Blurs’’, IEEE Trans. Signal Processing, 2024.

Commercial license only

Dataset generated by this simulator: https://xg416.github.io/DATUM/