Glassy state, a unique state of matter combining the rigidity of crystals with the random molecular structure of liquids, exhibits an array of challenging and poorly understood behaviors. Though useful, traditional models used to explain glassy state, often rely on phenomenological descriptions that do not highlight its fundamental physics. This gap in understanding has profound implications, not only for fundamental science but also for the myriad technological applications that depend on the unique properties of glassy materials, from everyday items like windowpanes and plastic bottles to advanced applications in electronics and biomedicine.

James Caruthers, the Gerald and Sarah Skidmore Professor of Chemical Engineering, along with collaborators from Purdue University Davidson School of Chemical Engineering, have published several significant studies that advance our understanding of the glass transition and the physics of the glassy state.

Historical research shows that as temperature is lowered, viscosity and the relaxation time of liquids both molecular and polymeric rapidly increase. This is illustrated in Fig. 1 for glycerol, where decrease in mobility is over 15 logarithmic decades for a temperature interval from 413 K to 183 K.  Eventually at the glass transition temperature, the material begins behaving like a solid and the relaxation time becomes longer than the experimentally accessible time. This is even though structurally the material remains amorphous resembling a high temperature liquid. Understanding the mechanism behind the slowing down of the mobility has remained one of the grand challenges for the condensed matter physics. Existing models for describing the log a vs T behavior, for example the celebrated WLF equation, are phenomenological, with multiple parameters lacking physical significance. 

Figure 1: Arrhenius plot for mobility of glycerol; factor ‘a’ is a compilation of viscosity, dielectric relaxation, and light scattering data

Professor Caruthers and his collaborators used a molecular dynamic (MD) simulation to search for the structural origins of the mobility behavior. An MD simulation was carried out of a prototypical glass former – a binary mixture of the Lennard-Jones particles, for which the ratio of the A and B particles, the radii and the interaction potential are chosen to avoid crystallization. The results are shown in Fig. 2 (left panel). Although the log"a"  range accessible in a simulation is inevitably smaller than the experimental one, the qualitative behavior is clearly captured, including the curvature indicating growth stronger than Arrhenian.  

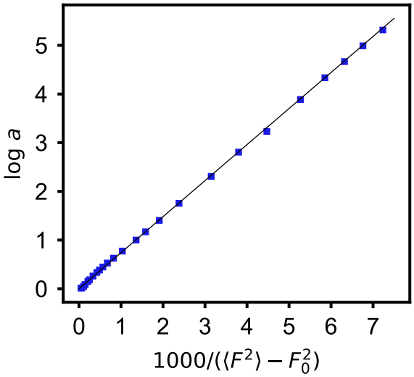
Fig. 2 (Left) Arrhenius plot for mobility of an 80:20 binary mixture of Lennard-Jones particles. (Right) Same mobility data vs mean squared force per particle. F₀² is the value of F²) at zero temperature.

Purdue researchers have found that the behavior of the log a for the entire data range can be described, as evidenced by linearization of the data, by mapping it to the average squared force per particle as shown in Fig. 2 (right panel). [J.C. Yungbluth et al “Unified description for the temperature dependence of mobility in liquids” J. Chem. Phys. 158, 164503 (2023)] For the first time a dynamic property of a glass forming system has been related to a structural property with clear physical meaning, thereby opening a path toward understanding the physics of glass formation.

Another long-standing unresolved problem has been the origin of the broad relaxation time spectrum observed in the glass forming materials. The spectrum is obtained using various experimental techniques, including the mechanical and dielectric relaxation, the light scattering and several other optical techniques, and the NMR. In the dielectric experiments the decay of the orientational correlator of molecular dipoles, C₁(t)=<cosθ(t))>, is probed, where θ(t)  is the angle between the dipole orientations at times 0 and t. Experimentally, the C₁(t)  exhibits a two-tier decay, where each tier, known as the β- and α-relaxation, is broader than a single-exponential process. There has been a plethora of empirical functions (stretched exponential, Cole-Cole, Cole-Davidson, Havrilyak-Negami) but not a single theoretical model which would produce such behavior.

Fig. 3 (Left) Schematic of the switchback model of rotational motion; example of the number of the switchback ramps Nr-7 is given. (Right) Rotational autocorrelator decay predicted by the switchback model; solid lines – predictions for increasing Nr. Dashed line – single-exponential decay.   

Recently, Grigori Medvedev, a research associate with the Davidson School of Chemical Engineering proposed a model which, for the first time, accounts for the experimentally observed relaxation response. [G.A. Medvedev “Unified description for the temperature dependence of mobility in liquids” Phys. Rev. E 107, 034122 (2023)]. In the model, the rotational motion of a dipole vector is idealized as a random walk along the path containing switchback ramps as depicted in Fig. 3 (left). An angular sector of size Y contains Nr ramps. The model allows for analytical solution where the predicted decay of the orientational correlator is shown in the Fig. 3 (right). As the number of the switchback ramps increases, a characteristic two-tier behavior emerges that is in qualitative agreement with the experiment. Importantly, increase in the relaxation time and the breadth of the spectrum under the switchback model is achieved without invoking any potential energy barriers, which were speculated about in the previous theories but not established experimentally. This new perspective shows that the key to the slowing down of mobility in glass formers is the tortuosity of the path a molecule must follow due to the dynamic constraints imposed by its neighboring molecules. 

The above papers represent a departure from the traditional approaches relying on just describing the data using empirical equations. The advances by the Purdue scientists are but first steps toward solving the old mystery of what happens to a material at a molecular level when it vitrifies.