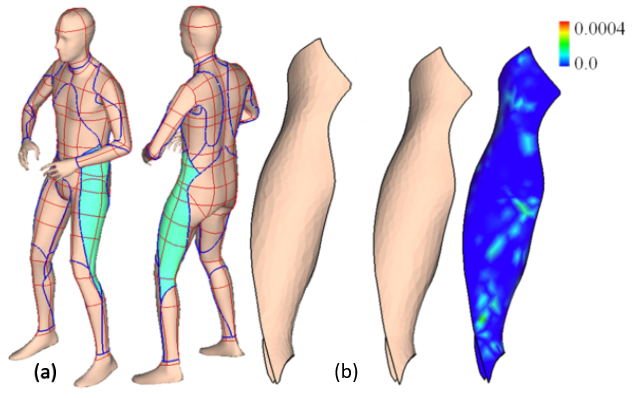
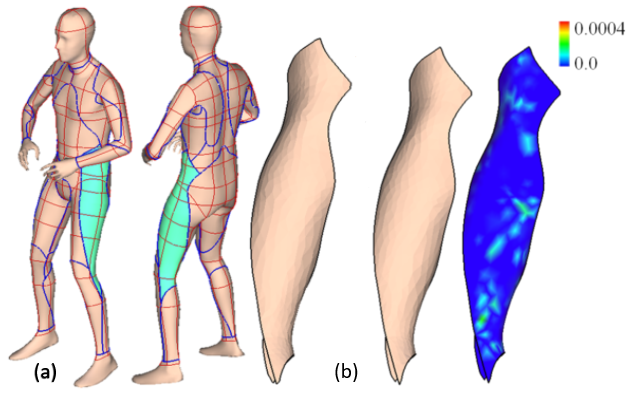
A flattenable mesh surface is a polygonal mesh surface that can be unfolded into a planar patch without stretching any polygon. This paper presents a new method for computing a slightly stretched flattenable mesh surface M from a piecewise-linear surface patch P∈R 3, where the shape approximation error between M and P is minimized and the strain of stretching on M is controlled. Prior approaches result in either a flattenable surface that could be quite different from the input shape or a (discrete) developable surface has relative simple shape. The techniques investigated in this paper overcome these difficulties. First, we introduce a new surface modeling method to conduct a sequence of nearly isometric deformations to morph a flattenable mesh surface to a new shape which has a better approximation of the input surface. Second, in order to get better initial surfaces for fitting and overcome topological obstacles, a shape perturbation scheme is investigated to obtain the optimal surface fitting result. Last, to improve the scalability of our optimal surface fitting algorithm, a coarse-to-fine fitting framework is exploited so that very dense flattenable mesh surfaces can be modeled and boundaries of the input surfaces can be interpolated.