Deep Ritz Method with Adaptive Quadrature for Linear Elasticity

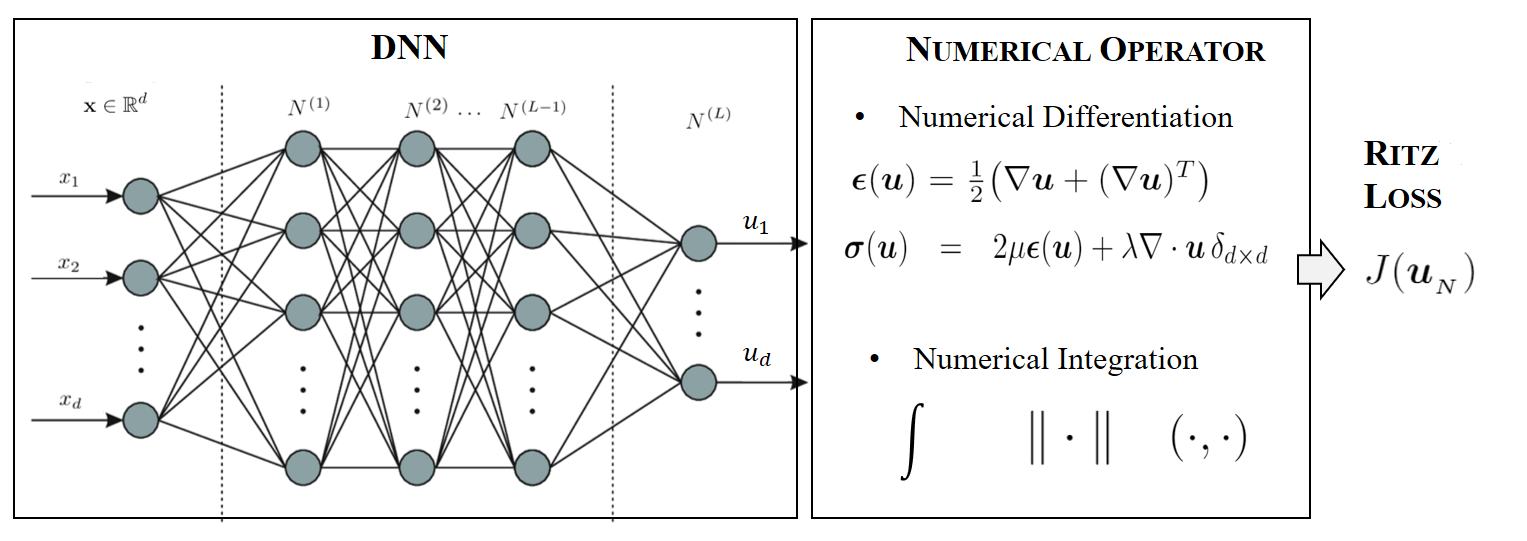
In this paper, we study the deep Ritz method for solving the linear elasticity equation from a numerical analysis perspective. A modified Ritz formulation using the H1/2(ΓD) norm is introduced and analyzed for linear elasticity equation in order to deal with the (essential) Dirichlet boundary condition. We show that the resulting deep Ritz method provides the best approximation among the set of deep neural network (DNN) functions with respect to the “energy” norm. Furthermore, we demonstrate that the total error of the deep Ritz simulation is bounded by the sum of the network approximation error and the numerical integration error, disregarding the algebraic error. To effectively control the numerical integration error, we propose an adaptive quadrature-based numerical integration technique with a residual-based local error indicator. This approach enables efficient approximation of the modified energy functional. Through numerical experiments involving smooth and singular problems, as well as problems with stress concentration, we validate the effectiveness and efficiency of the proposed deep Ritz method with adaptive quadrature.