Dual Neural Network (DuNN) method for elliptic partial differential equations and systems

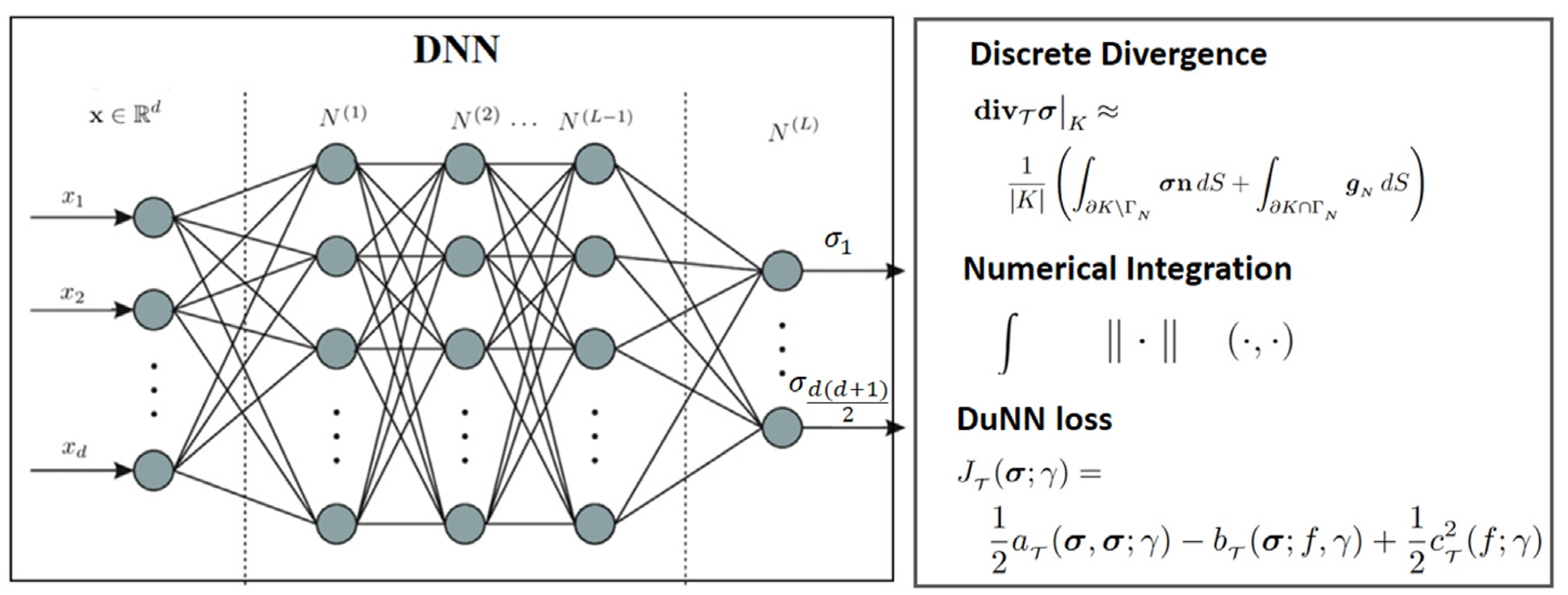
This paper presents the Dual Neural Network (DuNN) method, a physics-driven numerical method designed to solve elliptic partial differential equations and systems using deep neural network functions and a dual formulation. The underlying elliptic problem is formulated as an optimization of the complementary energy functional in terms of the dual variable, where the Dirichlet boundary condition is weakly enforced in the formulation. To accurately evaluate the complementary energy functional, we employ a novel discrete divergence operator. This discrete operator preserves the underlying physics and naturally enforces the Neumann boundary condition without penalization. For problems without reaction term, we propose an outer-inner iterative procedure that gradually enforces the equilibrium equation through a pseudo-time approach.