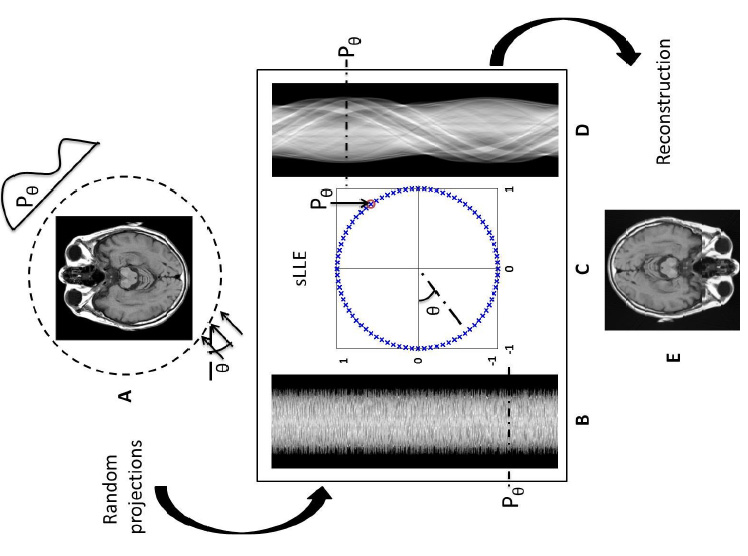
Abstract: The tomographic reconstruction of a planar object from its projections taken at random unknown view angles is a problem that occurs often in medical imaging. Therefore, there is a need to robustly estimate the view angles given random observations of the projections. The widely used locally linear embedding (LLE) technique provides nonlinear embedding of points on a flat manifold. In our case, the projections belong to a sphere. Therefore, we extend LLE and develop a spherical locally linear embedding (sLLE) algorithm, which is capable of embedding data points on a non-flat spherically constrained manifold. Our algorithm, sLLE, transforms the problem of the angle estimation to a spherically constrained embedding problem. It considers each projection as a high dimensional vector with dimensionality equal to the number of sampling points on the projection. The projections are then embedded onto a sphere, which parametrizes the projections with respect to view angles in a globally consistent manner. The image is reconstructed from parametrized projections through the inverse Radon transform. A number of experiments demonstrate that sLLE is particularly effective for the tomography application we consider. We evaluate its performance in terms of the computational efficiency and noise tolerance, and show that sLLE can be used to shed light on the other constrained applications of LLE.
Authors: Yi Fang, S.V.N. Vishwanathan, Mengtian Sun, and Karthik Ramani
Published in IEEE Computer Vision and Pattern Recognition (CVPR), pp 1077-1129, 2011
Download paper here