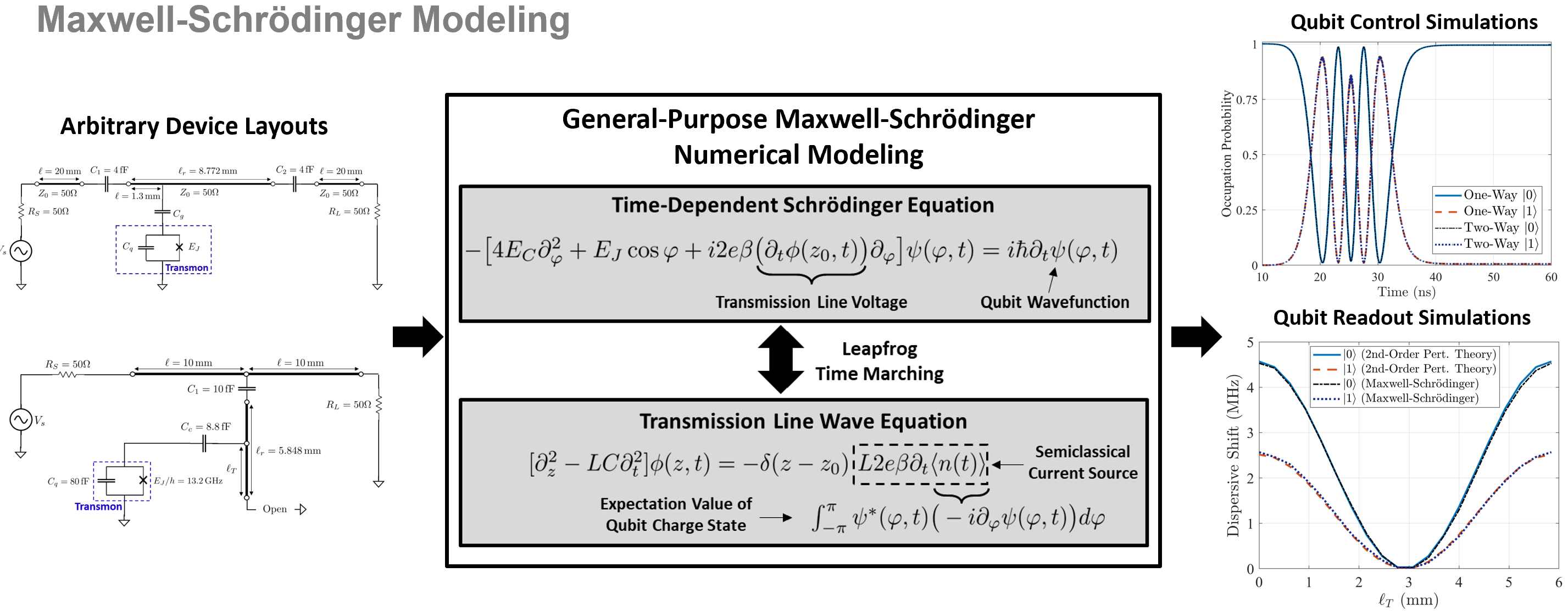
Semiclassical Modeling of Circuit Quantum Electrodynamics Devices

Circuit quantum electrodynamics (cQED) architectures are one of the most popular approaches currently being pursued to achieve a quantum advantage with quantum computers. However, modeling methods to perform the detailed engineering design of these systems are still in their infancy. To help improve the design process of cQED systems, it will be necessary to develop a tighter integration between rigorous full-wave computational electromagnetics solvers and the quantum analyzes necessary to assess quantum effects. One area where this can be more readily achieved is in the semiclassical analysis of cQED systems using Maxwell-Schrödinger modeling methods. In this analysis approach, the dynamics of the qubits of the system are evaluated in a quantum mechanical manner while the electromagnetic fields are still treated as classical quantities. This type of numerical approach has found great use in the analysis of certain optical systems, but has never been expored in the context of cQED systems up to this point.

Although semiclassical models invariably contain approximations to the full physics taking place, they can still find use in analyzing certain important effects at a much lower computational cost than a fully quantum mechanical analysis. For instance, semiclassical models of cQED systems can be useful in more rigorously analyzing qubit state preparation, the fidelity of various quantum gates, and the measurement of qubit states. This is possible because all of these operations involve applying a classical microwave pulse to various transmission lines that are coupled to the cQED qubits. One advantage of semiclassical models is that they can provide a self-consistent description of how the applied fields modify the qubit's state and how changes in the qubit state go on to modify the fields in the transmission lines. A nanoHUB app that allows users to explore the importance of these interactions in the context of controlling a transmon qubit's state is freely-available to allow users to study these concepts without needing to write or run any code. Importantly, this modeling approach allows one to analyze complex and arbitrary devices using the same method without requiring any new derivations or modifications to the underlying code. Additionally, the analysis has no quantum electromagnetic modes in the discretization of the Schrödinger equation, dramatically lowering the computational cost of simulating practical devices. We are currently using these methods to explore higher-fidelity optimization of qubit state readout pulses and the accompanying circuitry, with similar methods also applicable for optimizing control pulses. We are also working on rigorously modeling multi-qubit gates that generate quantum entanglement in this analysis framework.