- Research Projects
- High-Capacity Computational Electromagnetic Methods
- Electromagnetic Solutions for High-Frequency Mixed-Signal IC Design (Completed)
- Accurate and Fast Broadband Modeling of the Die-Package Interaction (Completed)
- A Hierarchical Matrix Framework for Electromagnetics-Based Analysis and Design of Next-Generation ICs (NSF)
- From O(N) to O(M): Scalable Algorithms for Large Scale Electromagnetics-Based Analysis and Design of Next Generation VLSI Circuits
- Simulation, Design and Fabrication of Interconnect Programmable Microwave Arrays (NSF, Completed)
- Rigorous and Fast Physics-Based Co-Simulation of Device-Structure-Material Interactions in Complex, Nonlinear, and Time-Variant Mixed-Signal Circuits (ONR, Completed)
- Direct Matrix Solutions of Linear Complexity for Rapid Modeling and Design of High Bandwidth Package Interconnects (SRC, Completed)
- Say "No" to Extraction - A Transformative Circuit Simulation Paradigm Guided by First Principles (NSF, Completed)
- Method for Fast and Accurate Signaling Analysis of Non-LTI Systems (Intel, Completed)
- Solution to a Few Open Problems in Inverse Design for High-Performance Integrated Circuit Synthesis in Full Electromagnetic Spectrum (DARPA, Completed)
- Multiphysics Simulation Algorithms and Experimental Methods for the Development of Cu/Graphene/TMD Hybrid Interconnect Solution (NSF, Completed)
- ERI Design: IDEA: Rapid Modeling and Analysis Framework for Full-Chip/Package/Board Layout Automation (DARPA, completed)
- Consortium for Electromagnetic Science and Technology (Synopsys, Cadence, Siemens, and Ansys)
- Limits to two-spin-qubit gate fidelity from vacuum fluctuations (DARPA, completed)
- Fast Method for High-Dimensional Global Optimization and Its Application to System Design Optimization (Intel)
- First-Principles Simulation of SKY130 Devices (Google)
- Open, Multiscale, Application-Agnostic Platform (Open-MAP) for Heterogeneous System-in-Package Co-Design (NSF)
- Rapid Heterogeneous Integration (Rapid-HI) Design Institute (Purdue Elmore ECE Emerging Frontiers Center)
- Readying TCAD for transient, DFT based quantum transport in the THz regime (DARPA)
- Research Highlights
Book mark: Direct FEM | Direct IE | Direct Electrically Large Analysis | Low-Frequency Breakdown | Explicit Unconditionally Stable | Circuit Simulator
Direct Finite Element Solver of Linear Complexity for Large-Scale Electromagnetic Analysis:
 In general, to solve problems with N parameters, the optimal computational complexity is linear complexity O(N). State-of-the-art fast finite-element solvers rely on iterative approaches to solve large-scale problems. The computational
complexity of an iterative solver is O(N_{it}N_{rhs}N) at best, where N_{it} is the number of iterations, and N_{rhs} is the number
of right hand sides. When N_{it} and N_{rhs} are large,
In general, to solve problems with N parameters, the optimal computational complexity is linear complexity O(N). State-of-the-art fast finite-element solvers rely on iterative approaches to solve large-scale problems. The computational
complexity of an iterative solver is O(N_{it}N_{rhs}N) at best, where N_{it} is the number of iterations, and N_{rhs} is the number
of right hand sides. When N_{it} and N_{rhs} are large, state-of-the-art iterative solutions become inefficient since the entire
iteration procedure has to be repeated for each right hand side. Furthermore, the complexity of an iterative solver is
problem dependent since the iteration number N_{it} is, in
general, problem dependent. In addition, most of the iterative
solvers rely on preconditioners to reduce N_{it}, which further
increases the overall computational complexity. The high computational complexity makes the analysis and design of many very
large-scale engineering systems beyond the reach of existing solvers. In this work, we pioneer a direct FEM solver of O(N) (optimal) complexity for general electromagnetic analysis.
state-of-the-art iterative solutions become inefficient since the entire
iteration procedure has to be repeated for each right hand side. Furthermore, the complexity of an iterative solver is
problem dependent since the iteration number N_{it} is, in
general, problem dependent. In addition, most of the iterative
solvers rely on preconditioners to reduce N_{it}, which further
increases the overall computational complexity. The high computational complexity makes the analysis and design of many very
large-scale engineering systems beyond the reach of existing solvers. In this work, we pioneer a direct FEM solver of O(N) (optimal) complexity for general electromagnetic analysis. 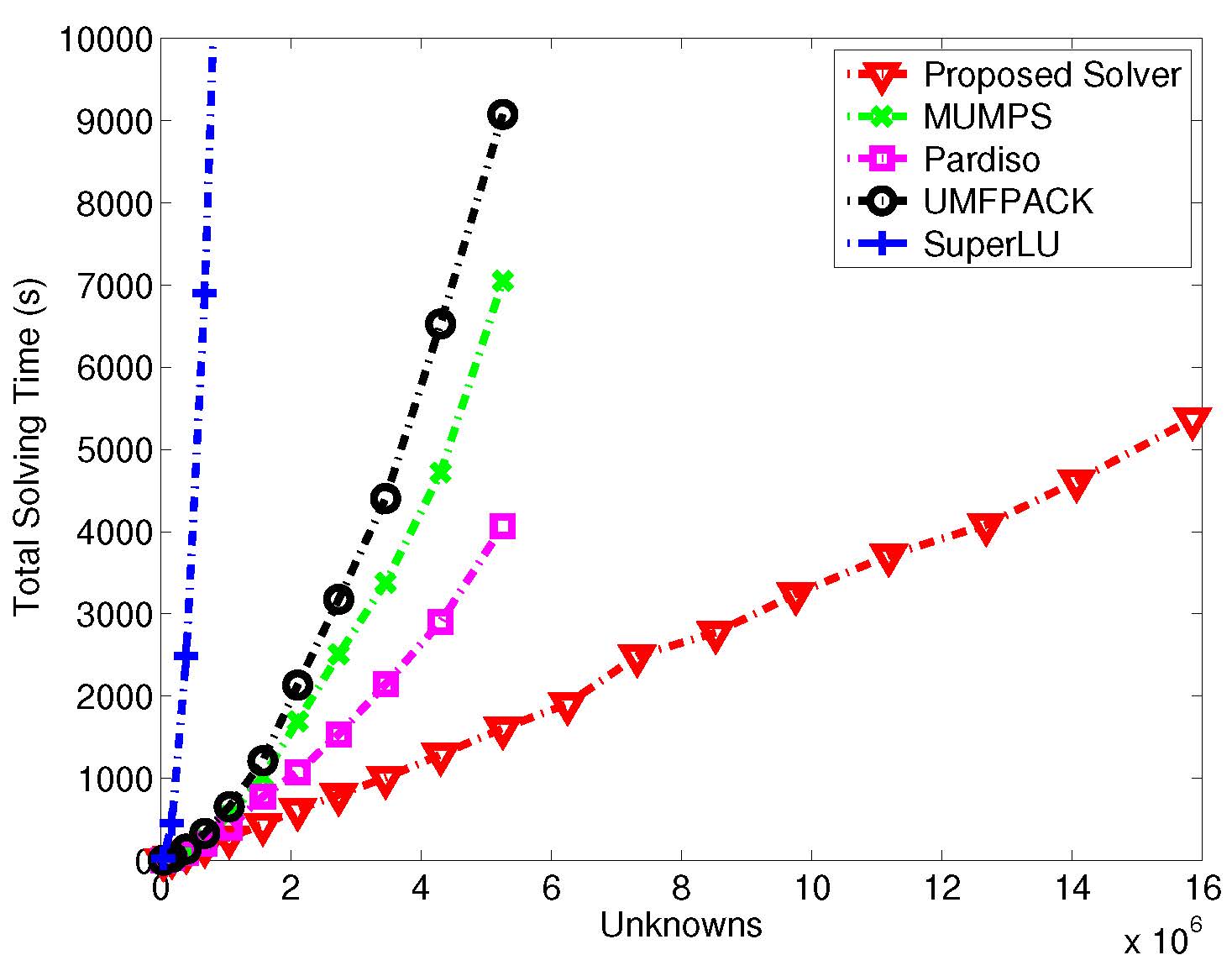 The linear complexity of this direct
solver in CPU time and memory consumption is demonstrated
by theoretical analysis and numerical experiments, for both electrically small and electrically large analyses. On a single 3 GHz CPU core, this solver has successfully solved an electrodynamic system matrix of over 22.8488 million unknowns resulting from an industry full package in 16 hours with first-principles-based full-wave accuracy;
it has also rapidly analyzed large-scale antenna arrays of over 73 wavelengths with 3,600 antenna elements having 10.1472 million unknowns, neither of which was feasible before. The upper right figure shows the electric field distribution generated by this direct solver across the entire package area, and the correlation of simulation results with measurements. The lower left figure provides a
time and complexity comparison with state-of-the-art direct sparse solvers. You can request a copy of this software on the "Software Release" page of this website.
The linear complexity of this direct
solver in CPU time and memory consumption is demonstrated
by theoretical analysis and numerical experiments, for both electrically small and electrically large analyses. On a single 3 GHz CPU core, this solver has successfully solved an electrodynamic system matrix of over 22.8488 million unknowns resulting from an industry full package in 16 hours with first-principles-based full-wave accuracy;
it has also rapidly analyzed large-scale antenna arrays of over 73 wavelengths with 3,600 antenna elements having 10.1472 million unknowns, neither of which was feasible before. The upper right figure shows the electric field distribution generated by this direct solver across the entire package area, and the correlation of simulation results with measurements. The lower left figure provides a
time and complexity comparison with state-of-the-art direct sparse solvers. You can request a copy of this software on the "Software Release" page of this website.
Selected Publications:
[4] B. Zhou and D. Jiao, "Linear (Optimal) Complexity Direct Full-Wave Solution of Full-Package Problems Involving over 10 Million Unknowns on a Single Computer," TECHCON 2014. (BEST PAPER AWARD, Chip-Package co-design session)
Direct Integral Equation Solvers (Inverse and LU) of Linear Complexity for Large-Scale Circuit Extraction:
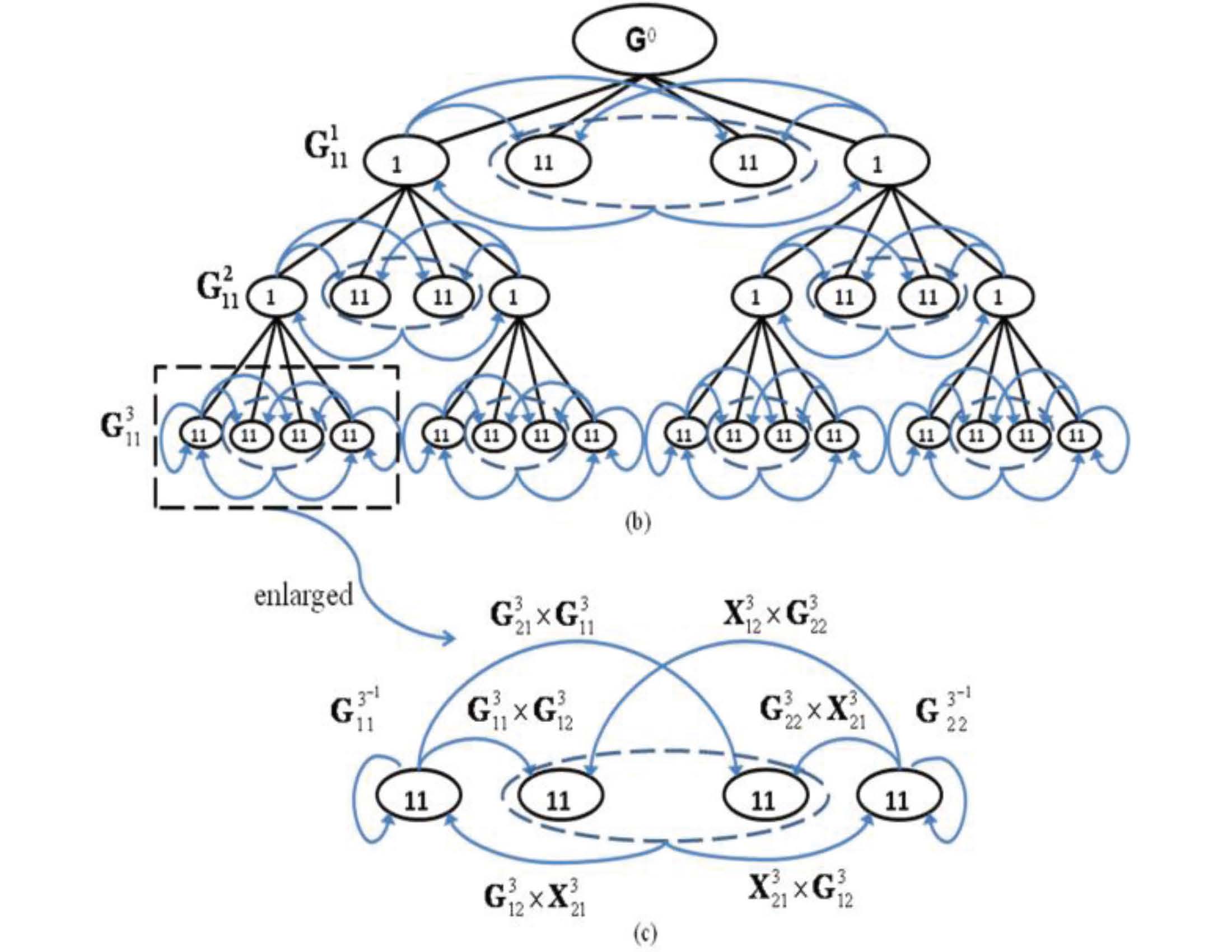 Prevailing fast integral equation (IE) solvers are iterative solvers relying on fast techniques that can
perform a dense matrix-vector multiplication in O(N) or O(NlogN) complexity. The complexity of an iterative solver is at best O(N_{rhs}N_{it}N), where
N_{it} is the number of iterations, and N_{rhs} the number of right hand sides. We have originated linear (optimal) complexity dense matrix inversion and LU factorization algorithms for general 3-D circuit extraction, including capacitance, resistance, inductance,
and full-wave extraction of general 3-D structures involving inhomogeneous dielectrics and arbitrarily shaped lossy conductors.
This work breaks the conventional computational barrier of IE-based methods.
Prevailing fast integral equation (IE) solvers are iterative solvers relying on fast techniques that can
perform a dense matrix-vector multiplication in O(N) or O(NlogN) complexity. The complexity of an iterative solver is at best O(N_{rhs}N_{it}N), where
N_{it} is the number of iterations, and N_{rhs} the number of right hand sides. We have originated linear (optimal) complexity dense matrix inversion and LU factorization algorithms for general 3-D circuit extraction, including capacitance, resistance, inductance,
and full-wave extraction of general 3-D structures involving inhomogeneous dielectrics and arbitrarily shaped lossy conductors.
This work breaks the conventional computational barrier of IE-based methods.  In our direct surface IE solver for capacitance
extraction, a dense matrix having 3.71 million unknowns is inverted in fast CPU time (1.6 h), modest memory consumption (4.4 GB),
and with prescribed accuracy satisfied on a single core running at
3 GHz. In our O(N) direct surface IE solvers as well as O(N) direct volume IE solvers for full-wave extraction, we overcome the
numerical challenge of solving a highly unstructured system matrix mixed with both square and rectangular dense
and sparse matrices by developing a fast linear complexity
direct solution. The inverse of a 2.68-million-unknown matrix
arising from the full-wave extraction of a large-scale 3-D interconnect, which is a matrix solution for 2.68 million right hand sides,
was obtained in less than 1.5 GB memory and 1.3 h on a single 3 GHz CPU core. Comparisons with both state-of the-art iterative and direct IE solvers for circuit extraction
have demonstrated clear advantages of the O(N) direct IE solvers in both CPU time and memory consumption.
In our direct surface IE solver for capacitance
extraction, a dense matrix having 3.71 million unknowns is inverted in fast CPU time (1.6 h), modest memory consumption (4.4 GB),
and with prescribed accuracy satisfied on a single core running at
3 GHz. In our O(N) direct surface IE solvers as well as O(N) direct volume IE solvers for full-wave extraction, we overcome the
numerical challenge of solving a highly unstructured system matrix mixed with both square and rectangular dense
and sparse matrices by developing a fast linear complexity
direct solution. The inverse of a 2.68-million-unknown matrix
arising from the full-wave extraction of a large-scale 3-D interconnect, which is a matrix solution for 2.68 million right hand sides,
was obtained in less than 1.5 GB memory and 1.3 h on a single 3 GHz CPU core. Comparisons with both state-of the-art iterative and direct IE solvers for circuit extraction
have demonstrated clear advantages of the O(N) direct IE solvers in both CPU time and memory consumption.
Selected Publications:
Direct Integral Equation Solvers for Electrically Large Analysis:
Unlike electrically small problems, the rank of an electrodynamic IE operator increases with electric size for achieving a prescribed accuracy, which results in a higher computational complexity if no advanced algorithms are conceived to effectively manage the rank's growth with electric size. The true indicator of this rank's growth is singular value decomposition (SVD), which is computationally O(N^3) and is thus not used explicitly.
Prevailing source-observer separated representations of the IE operator adopted by existing fast IE solvers do not lead to a minimal rank representation required by accuracy. These representations include interpolation-based, Taylor series expansion based, plane wave expansion based methods, etc. In fact, these representations result in a full-rank representation of the IE operator for electrically large problems, which makes the compression of the IE operator sub-optimal for general electrodynamic analysis.
In view of the pivotal importance of the rank of the off-diagonal blocks in an IE operator, we have carried out a theoretical study on its growth with electric size in integral equations. The significance of this study lies in the fact that it derives a closed-form analytical expression of the rank of the coupling Green's function, which has the same scaling as that depicted by SVD-based rank revealing. The findings on the rank are summarized as follows:
1- The rank (r) of the off-diagonal block, irrespective of the electric size, is far less than the size of the block (m), thus the off-diagonal block has a low rank representation i.e. r << m.
2- For electrically small and one-dimensional configurations of sources and observers, the rank required by a prescribed accuracy remains constant irrespective of the problem size.
3- For 2- and 3-D configurations, the rank varies as square root of logarithm and linearly with the electric size, respectively.
Based on the above findings, we have developed fast direct integral equation solvers for electrically large analysis. In our direct surface IE solvers, a dense matrix for a 96-wavelength problem with over 1 million unknowns was directly factorized in 20 hours with 85-seconds LU solution time on a single 3 GHz CPU core. In our electrically large volume IE solver, we have achieved O(N) complexity in matrix-vector multiplication, and O(NlogN) complexity in inverse irrespective of electrical size.
Selected Publications:
Low-Frequency Breakdown:
 A full-wave solution of Maxwell's equations breaks down at low frequencies, which was observed as early as when the area of
Computational EM came into existence. The same breakdown is observed when there exist dense discretizations or fine features relative to working wavelength. This problem is very critical in today's engineering problems analyzed via EM simulators. This is
not only because the breakdown frequency of full-wave solvers can fall right within the operating frequencies of an engineering product, but also
because there could exist a range of frequencies in which the solution to Maxwell's equations is unknown, since a full-wave solver breaks down
while static- and quasi-static solutions are invalid especially in highly multiscaled problems. The root cause of low-frequency breakdown is
finite machine precision, thus the problem is very challenging to solve. We are able to overcome the barrier imposed by the finite machine precision,
and successfully find the solution to the original full-wave system of equations from an arbitrarily high electrodynamic frequency all the way down to
zero frequency. Our solution is applicable to both PDE- and IE-based methods.
A full-wave solution of Maxwell's equations breaks down at low frequencies, which was observed as early as when the area of
Computational EM came into existence. The same breakdown is observed when there exist dense discretizations or fine features relative to working wavelength. This problem is very critical in today's engineering problems analyzed via EM simulators. This is
not only because the breakdown frequency of full-wave solvers can fall right within the operating frequencies of an engineering product, but also
because there could exist a range of frequencies in which the solution to Maxwell's equations is unknown, since a full-wave solver breaks down
while static- and quasi-static solutions are invalid especially in highly multiscaled problems. The root cause of low-frequency breakdown is
finite machine precision, thus the problem is very challenging to solve. We are able to overcome the barrier imposed by the finite machine precision,
and successfully find the solution to the original full-wave system of equations from an arbitrarily high electrodynamic frequency all the way down to
zero frequency. Our solution is applicable to both PDE- and IE-based methods. 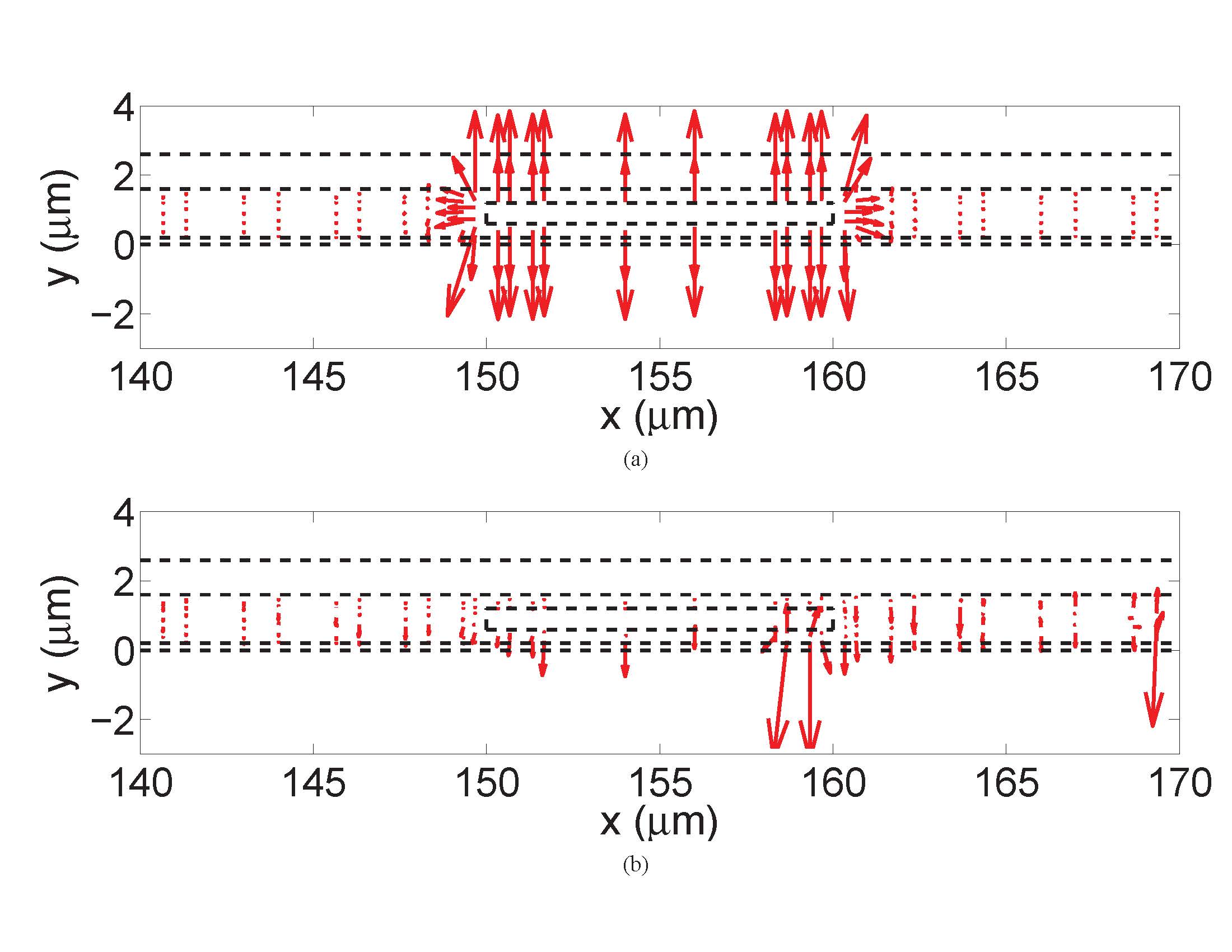 A fast method is also developed to speed up the low-frequency computation
in a reduced system of O(1). Moreover, we have demonstrated, both theoretically and numerically, that although the problem is termed low-frequency breakdown, the solution at breakdown frequencies
can be a full-wave solution for which static and quasi-static assumptions are invalid for use. This is especially true in multi-scale problems,
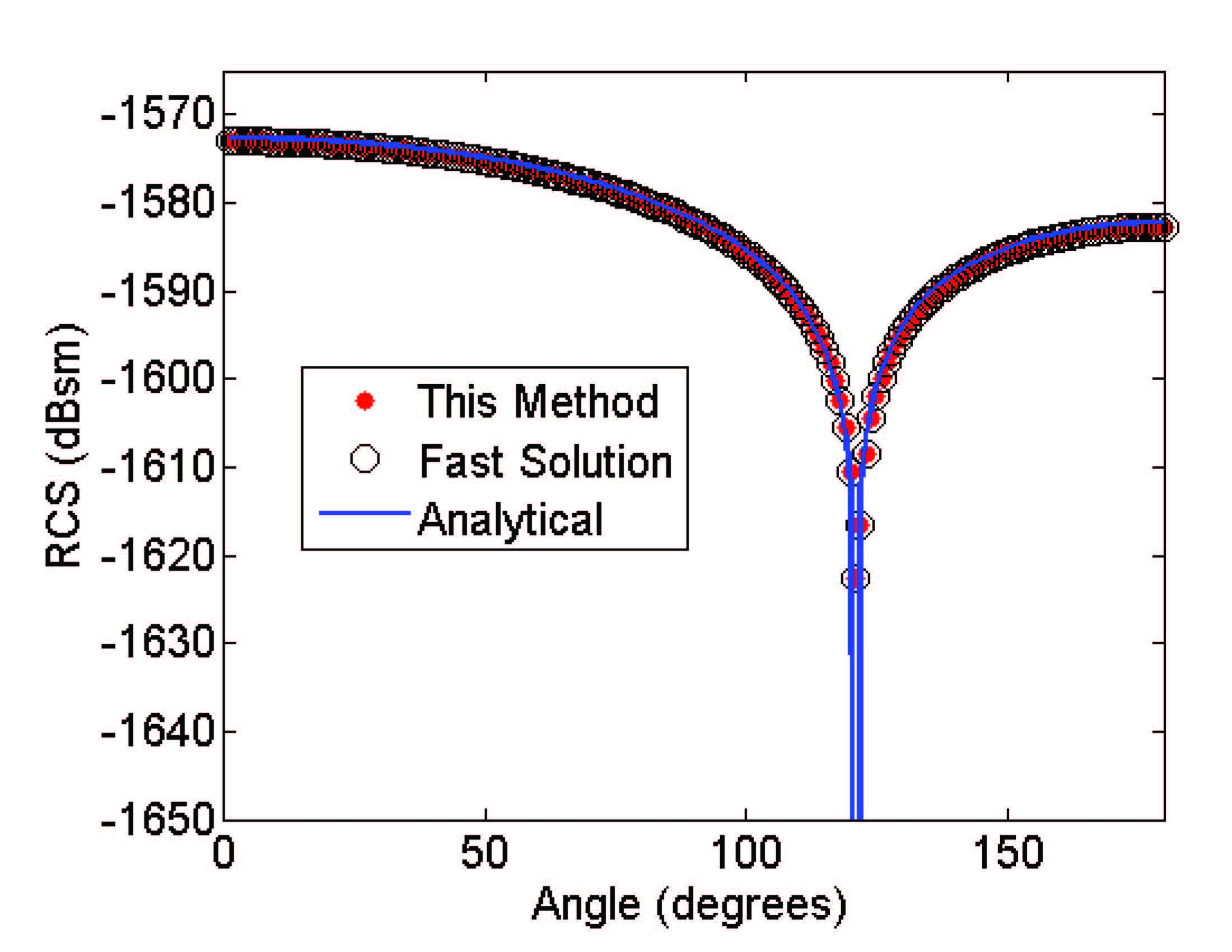
the geometrical scales of which are many orders of magnitude different. The upper right figure illustrates the RCS of a sphere of 1 m radius at 1e-32 Hz generated by the proposed method
in comparison with analytical data. The lower left figure shows the electric field distribution of an on-chip interconnect structure at 1 Hz generated by the proposed method (upper subfigure) in
comparison with the field distribution obtained by a conventional method (lower subfigure).
A fast method is also developed to speed up the low-frequency computation
in a reduced system of O(1). Moreover, we have demonstrated, both theoretically and numerically, that although the problem is termed low-frequency breakdown, the solution at breakdown frequencies
can be a full-wave solution for which static and quasi-static assumptions are invalid for use. This is especially true in multi-scale problems,
the geometrical scales of which are many orders of magnitude different. The upper right figure illustrates the RCS of a sphere of 1 m radius at 1e-32 Hz generated by the proposed method
in comparison with analytical data. The lower left figure shows the electric field distribution of an on-chip interconnect structure at 1 Hz generated by the proposed method (upper subfigure) in
comparison with the field distribution obtained by a conventional method (lower subfigure).
[5] J. Zhu and D. Jiao, "Solution to the low-frequency breakdown problem in computational electromagnetics," Chapter 8 in the Computational Electromagnetics: Recent Advances and Engineering Applications edited by Raj Mittra. Springer, 2013, pp. 259-316.
Explicit and Unconditionally Stable Time-Domain Methods:
The time-domain methods in computational electromagnetics can be categorized into two classes.
One is the explicit time-domain method; the other is the implicit time-domain method.
Explicit methods can avoid solving a matrix, while implicit methods generally require a matrix solution. The time step of a traditional explicit method is
restricted by the smallest space step for ensuring the stability of a time-domain simulation. Existing unconditionally stable methods are all implicit methods.
 This problem has prevented the existing
time-domain methods from analyzing large-scale multiscaled problems in feasible run time and memory, where fine features can be orders of magnitude smaller than the largest feature size. In this work, we create explicit time-domain methods that are unconditionally stable, which removes a major limit in time-domain analysis.
The method retains the strength of an explicit time-domain method in being matrix free, while eliminating its shortcoming in time step when the smallest space step
is small as compared to the working wavelength. In the example shown in the figure, a conventional explicit method requires a time step as small as 1.0363e-15 s
to be stable, whereas the time step required by sampling accuracy for the input spectrum is 13 orders of magnitude larger. As shown in the figure, first,
the proposed method is stable regardless of the choice of the time step; second, it is capable of using the time step solely determined by sampling accuracy to generate accurate results.
This problem has prevented the existing
time-domain methods from analyzing large-scale multiscaled problems in feasible run time and memory, where fine features can be orders of magnitude smaller than the largest feature size. In this work, we create explicit time-domain methods that are unconditionally stable, which removes a major limit in time-domain analysis.
The method retains the strength of an explicit time-domain method in being matrix free, while eliminating its shortcoming in time step when the smallest space step
is small as compared to the working wavelength. In the example shown in the figure, a conventional explicit method requires a time step as small as 1.0363e-15 s
to be stable, whereas the time step required by sampling accuracy for the input spectrum is 13 orders of magnitude larger. As shown in the figure, first,
the proposed method is stable regardless of the choice of the time step; second, it is capable of using the time step solely determined by sampling accuracy to generate accurate results.
Selected Publications:
[3] M. Gaffar and D. Jiao, "An Alternative Method for Making an Explicit FDTD Unconditionally Stable," IEEE International Microwave Symposium, 2015.
[4] W. Lee and D. Jiao, "A New Explicit and Unconditionally Stable Time-Domain Finite-Element Method," IEEE Int. Symposium Antennas and Propagation, 2015.
Extraction-Free Circuit Simulators:
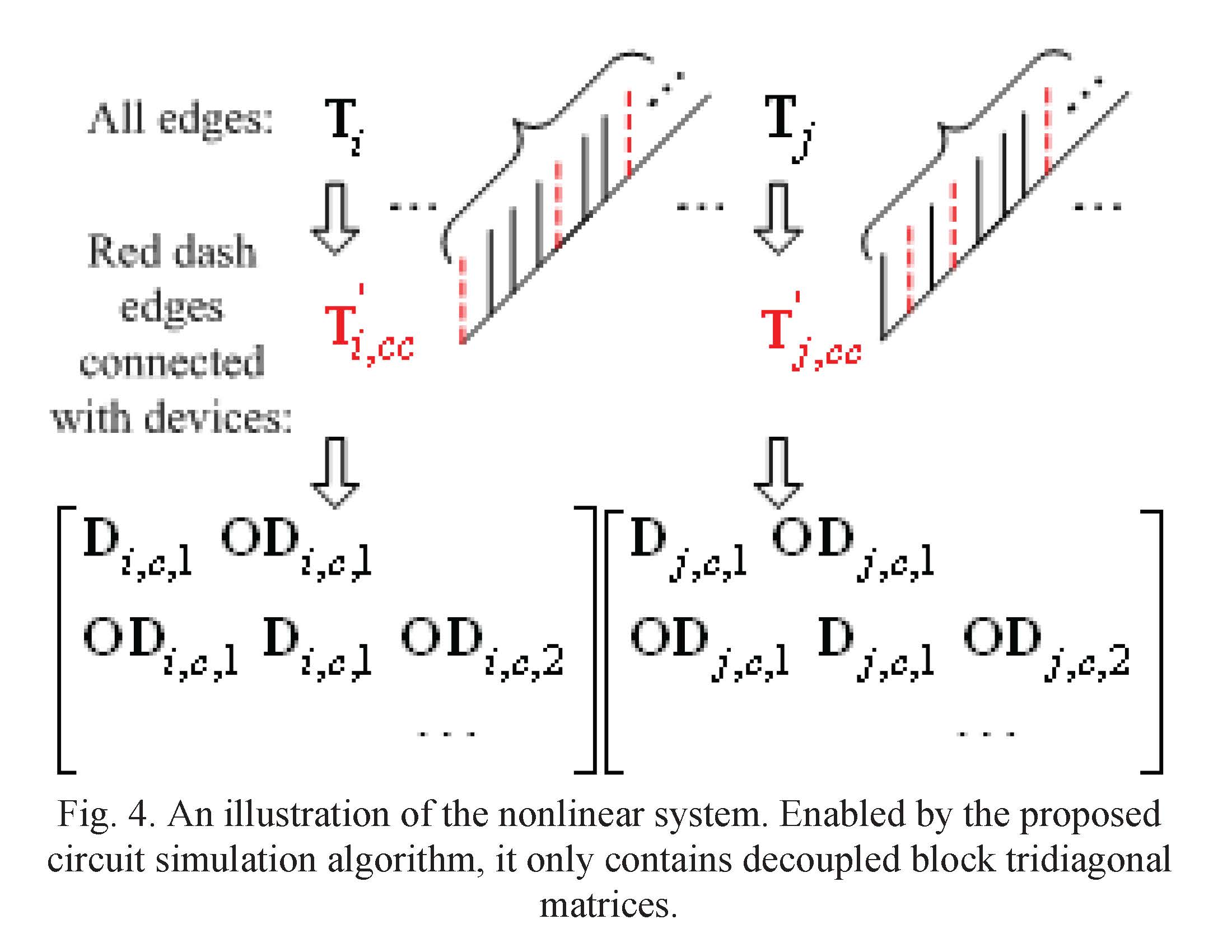 The prevailing circuit simulation paradigm involves first the extraction of the linear network. The extracted model of the linear network is then stitched
with the nonlinear devices for the simulation of the entire circuit. Besides various inaccuracy issues due to circuit extraction and the stitching of circuit
models, existing circuit simulators have not achieved optimal complexity. We developed an extraction-free circuit simulator that bypasses circuit extraction
altogether. Guided by electromagnetics-based first principles,
The prevailing circuit simulation paradigm involves first the extraction of the linear network. The extracted model of the linear network is then stitched
with the nonlinear devices for the simulation of the entire circuit. Besides various inaccuracy issues due to circuit extraction and the stitching of circuit
models, existing circuit simulators have not achieved optimal complexity. We developed an extraction-free circuit simulator that bypasses circuit extraction
altogether. Guided by electromagnetics-based first principles,  this extraction-free simulator has not only accomplished an optimal complexity
both in time and space, but also offered uncompromised accuracy and linear speedup in parallelization, overcoming the shortcomings of the existing
extraction-based circuit simulation frameworks. Application to die-package co-simulation as well as very large-scale on-chip circuits
involving close to 1 million CMOS transistors and interconnects having hundreds of millions of unknowns has demonstrated the
superior performance of the new extraction-free circuit simulator.
this extraction-free simulator has not only accomplished an optimal complexity
both in time and space, but also offered uncompromised accuracy and linear speedup in parallelization, overcoming the shortcomings of the existing
extraction-based circuit simulation frameworks. Application to die-package co-simulation as well as very large-scale on-chip circuits
involving close to 1 million CMOS transistors and interconnects having hundreds of millions of unknowns has demonstrated the
superior performance of the new extraction-free circuit simulator.
Selected Publications:
