Lattice Properties of Nanostructures
This page gives an overview on how NEMO and OMEN calculate lattice properties.
Valence Force Field (VFF) Model
We derive static and dynamic lattice properties from the following expression for the crystal energy:

Here U is the total energy of the crystal, i,j,k,l are indices that run over all atoms in the structure, rij and dij are the actual and ideal lengths of the bond between atoms i and j, theta0 is the ideal bond angle, Zi and Zj are pointlike effective charges and alpha,beta,gamma,delta,nu are the orce constants. NN stands for nearest-neighbor and COP(j-i-k-l) stands for the condition that the bonds j-i, i-k and i-l need to be connected and coplanar.
The valence force field model is described by the first three lines of the expression for U, which are repulsive short-range interactions that depend on bond lengths and bond angles. For 0D and 3D structures (bulk crystals and quantum dots) we augment this model by the long-range, attractive Coulomb interaction (last line) within a rigid ion approximation. This approximation assumes that the combination of core and electron orbital charge distribution around an atom can be replaced with a single, fractional, pointlike charge at the atom center that follows rigidly (i.e., without change in magnitude) the atomic oscillations. For 3D-periodic structures the Coulomb interaction can be treated exactly using Ewald summation.
Many flavors of the VFF model exist. A large number of investigations consider only the terms alpha and beta, known as the Keating model. However, it can be shown that this model has discrepancies to experimental values for the elastic constants, the phonon dispersion and volume expansion parameters such as the Grueneisen coefficients.
Strain Relaxation in Nanostructures
The (static) relaxed positions of the atoms are found from the condition that the energy U is minimal.
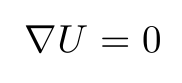
Here the derivative is taken with respect to the 3N displacement coordinates of the explicitly considered N atoms.
Phonon Modes in Nanostructures
The dynamic properties of the structure are described in terms of phonons, i.e. harmonic lattice vibrations. Phonon modes and energies are the eigenstates and eigenvalues of the dynamical matrix:
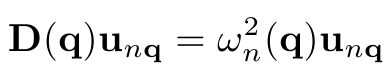
Here D is the dynamical matrix, q is the phonon wavevector, n is the phonon branch (e.g. n=1...6 for bulk crystals with a 2-atomic basis), u is the phonon amplitude oscillation vector and w is the phonon frequency. The dynamical matrix is connected to the total crystal energy as:
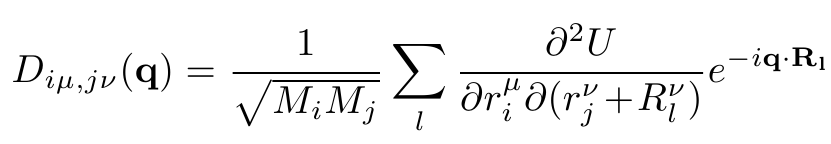
Here Mi and Mj are the masses of atoms i and j, mu and nu are spatial indices (x,y,z) and Rl is a Bravais lattice vector.
