Code and Data
As listed below, some of our code and data are made available to public. We believe that wide dissemination of research papers, code, and data (whenever possible and appropriate) is of fundamental importance for humanity to accumulate our knowledge and advance science and technology.
If you have questions or find bugs, please send them to the developer/author, with koguri@purdue.edu cc-ed.
SCvx* (scvx-star) & Adaptive-mesh SCP
Developer/Author:
Naoya Kumagai (nkumagai@purdue.edu)
Description:
An implementation of SCvx* (scvx-star) algorithm, which extends an algorithm called SCvx, to provide guaranteed convergence to a local feasible optimum for general non-convex optimal control problems.
The repository includes the application of SCvx* to nonlinear space trajectory optimization, both with impulsive and low-thrust engines.
The repo also includes an implementation of the adaptive-mesh sequential convex programming (AMSCP) method based on SCvx*, which optimizes the discretization node epochs for better optimality and for allowing the user to optimize the epoch of events, such as planetary gravity assists and encounters with celestial bodies.
Link to code and data:
Relevant images:
Comparison of SCvx* and SCvx
Adaptive-mesh SCP with SCvx* applied to low-thrust and impulsive trajectory optimization for Ceres sample return mission
Relevant papers:
- K. Oguri. Successive Convexification with Feasibility Guarantee via Augmented Lagrangian for Non-Convex Optimal Control Problems. In IEEE Conference on Decision and Control (CDC), 2023 (arXiv version with some corrections: https://arxiv.org/abs/2304.14564)
- N. Kumagai and K. Oguri. Adaptive-Mesh Sequential Convex Programming for Space Trajectory Optimization. AIAA Journal of Guidance, Control, and Dynamics, 2024, doi: 10.2514/1.G008107
If you use our code or develop your code based on our code/papers, please cite these papers appropriately (1: SCvx* and 2: AMSCP).
Trajectory optimization under uncertainty with NLP
Developer/Author:
Jerry Vaghese (varghes5@purdue.edu)
Description:
A nonlinear programming approach to trajectory optimization under Gaussian uncertainty using SNOPT.
The implementation supports orbit-to-orbit or point-to-point transfers in the two-body problem and three-body problem with initial state Gaussian dispersion, stochastic acceleration, and control execution error.
This implementation incorporates feedback gain parametrization, which greatly reduces the number of free variables traditionally associated with linear feedback policy optimization for covariance steering, and gravity limiting, which prevents numerical integration failure due to point mass singularities in the equations of motion.
The code also includes toggleable collision avoidance path constraints (both deterministic and stochastic) evaluated at segment boundaries.
Link to code and data:
Relevant images:
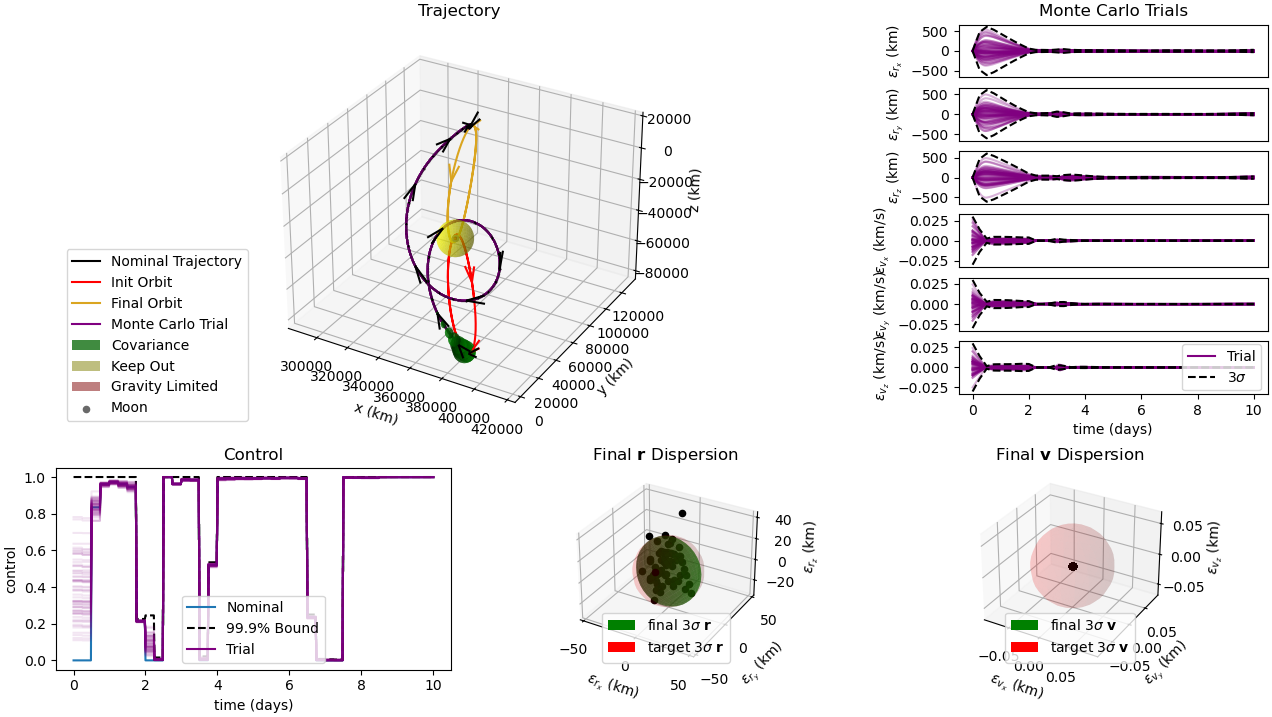
Statistical Trajectory Optimization with Deterministic Collision Avoidance
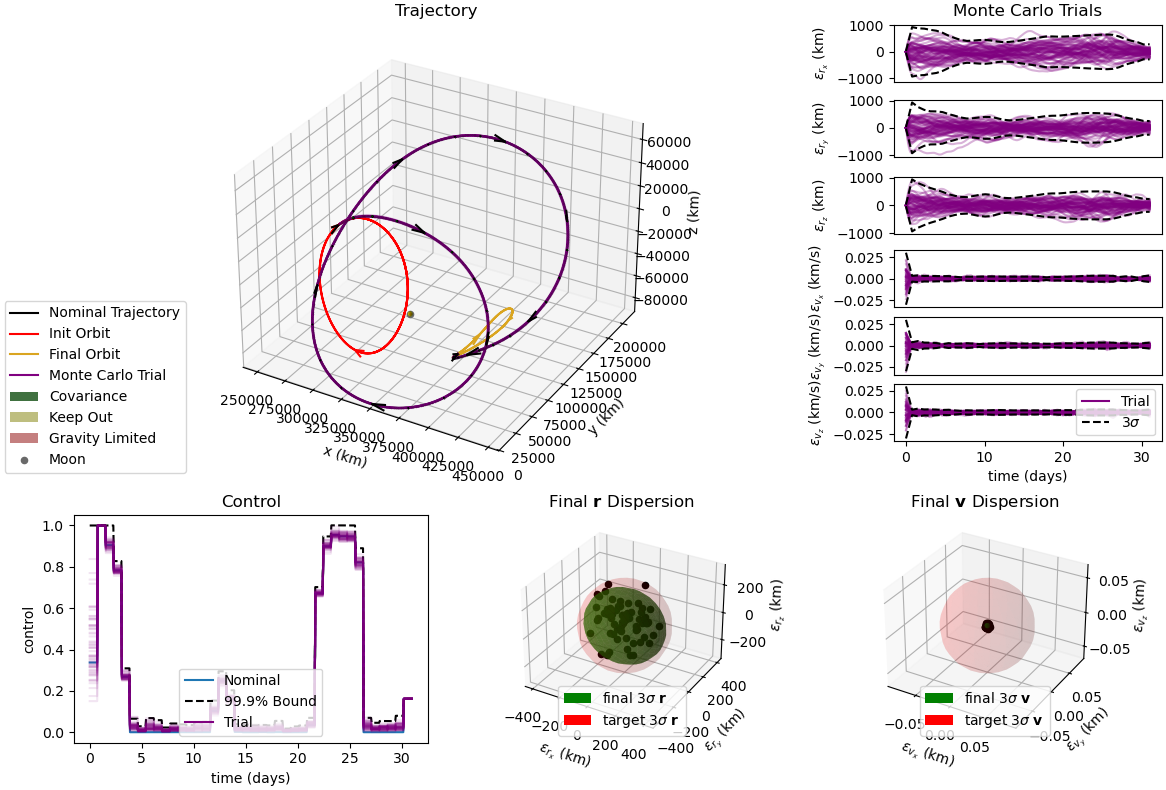
L1 to L2 Statistically Optimal Trajectory with Higher Execution Error/Larger Final Covariance

