.
.
.
.
.
ME 49601 - Introduction to Computational Fluid Dynamics
This is a new experimental course being offered for the first time in Spring 2018.
Course Announcement Flyer
Objectives
By the end of the semester students will be able to set up and solve common fluid dynamic problems with popular commercial software, such as ANSYS Fluent, while also being able to appropriately discretize governing fluid dynamic equations for very simple flow problems, inspired by problem sets from ME309 (Fluid Mechanics). Special emphasis will be placed on correctly interpreting the results of these simulations to understand the physics of the problem being modeled.
Topics
- Review of Fundamental Fluid Mechanics
- Advection and Diffusion
- Navier-Stokes Equations
- Laminar and Turbulent Flows
- Fluid Machinery and Compressible Flows
ME614 - Computational Fluid Dynamics
Prerequisites
Prerequisites for the course include basic knowledge of fluid mechanics, linear algebra, partial differential equations and average (not beginner!) programming skills. The use of Python is strongly recommended but not mandatory. The class content is structured in such a way to allow talented undergraduate students to successfully complete the coursework.
Prerequisites for the course include basic knowledge of fluid mechanics, linear algebra, partial differential equations and average (not beginner!) programming skills. The use of Python is strongly recommended but not mandatory. The class content is structured in such a way to allow talented undergraduate students to successfully complete the coursework.
Objectives
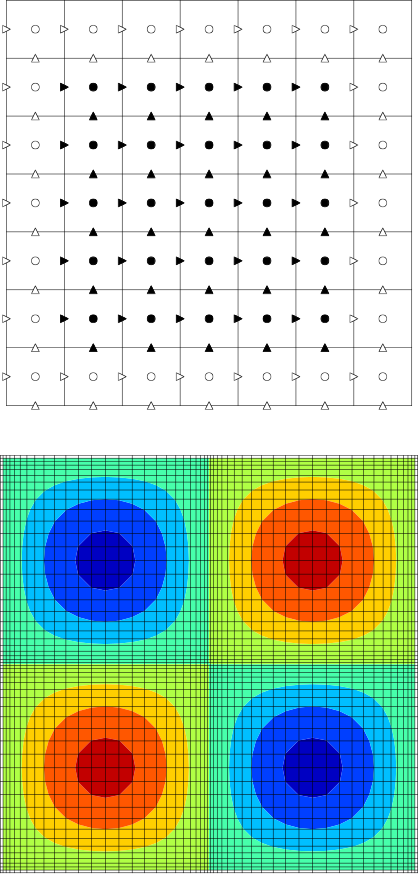
The course will cover traditional aspects of Computational Fluid Dynamics (CFD) with focus on momentum and mass transfer applications, while providing exposure to the latest generation of high-level dynamic languages and version-control software. The course will cover the following topics:
- Spatial & Temporal Discretizations
- Linear Advection & Diffusion Equation
- Poisson and Heat Equations
- Navier-Stokes Solvers
- Introduction to Compressible Flow
.
.
ME 608 - Numerical Methods In Heat, Mass, And Momentum Transfer
Objectives
The course focuses on the finite volume method and its use in the analysis of fluid dynamics, heat and mass transfer problems. A general framework for the discretization of convection-diffusion equations is developed for both structured and unstructured meshes.
Topics
- Mesh Generation, Discretization
- Linear Algebra, Poisson Equation
- Time Advancement Schemes, Unsteady Heat Transfer
- Navier-Stokes Solvers on Unstructured Grids
- Advanced topics: Linear-Stability Theory, Block-Spectral solvers, Finite-Element Methods, etc.
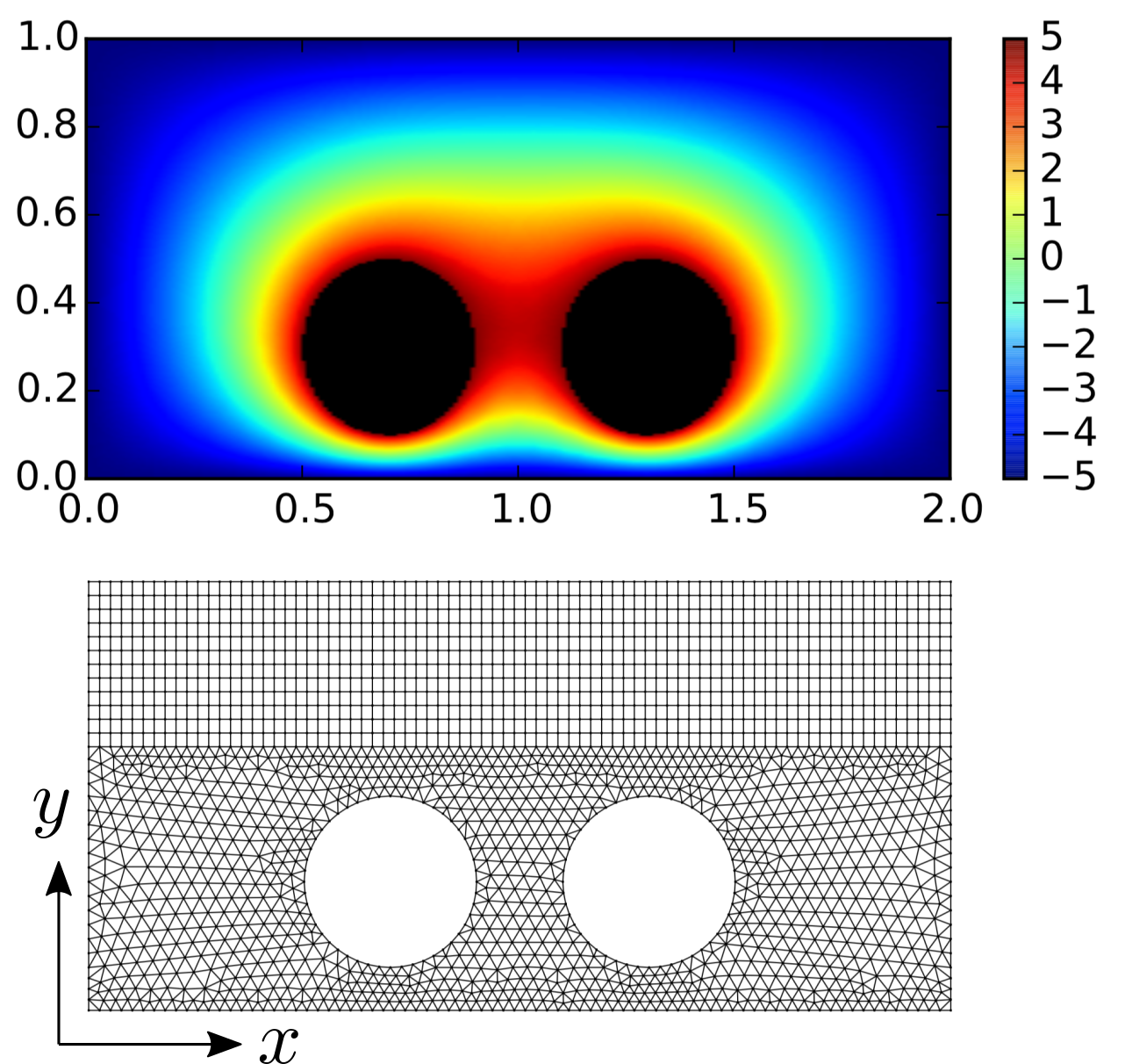Hybrid computational mesh (bottom) and color contour of temperature field (bottom) from a two-dimensional unstructured heat-transfer solver (Lucas E O'Neill, ME608-Fall 2017)
.
.