Flow Resolution
News in 2016-2017 from Prof. Poggie's research group.
The Falling Slinky Problem
As the Slow Mo Guys show, if you hold a Slinky by one end, and let go, the top of the slinky falls, but the bottom stays in place. The same thing goes for a chain, a spring, and even a solid bar. Why? I know others have solved this problem, but it's fun to try to figure it out for yourself. Here is my analysis of the problem.
Poggie and Deshpande interviewed by RCAC
Professor Jonathan Poggie and MS student Akshay Deshpande were recently interviewed for a article highlighting their use of the Halstead Cluster at Purdue's Rosen Center for Advanced Computing (RCAC): Halstead cluster is aeronautics professor’s 21st century wind tunnel
How cool is a flying aircraft carrier?
I assigned another extra credit project for AAE 33400 for the fall 2016 semester, an analysis of the Helicarrier. In the Marvel Avengers movies, the S.H.I.E.L.D. Helicarrier is a kind of flying aircraft carrier. It can sail on the ocean like a conventional ship, but can also lift out of the water and fly.
My challenge to the students in AAE 33400 was to analyze the operation of the Helicarrier. I wanted to know if the lift fans could support the vehicle, and what speed the array of engines in back could produce. The original problem and my solution are here:
The upshot is that the Helicarrier as depicted in the movies is not feasible. It is far too heavy to fly. (Surprised?) Nonetheless, a redesign with larger fans and substantially reduced weight looks promising.
If I were advising S.H.I.E.L.D. on purchases of military equipment, I would have to recommend reconsideration of the Helicarrier. We have to assume that the cost of one unit would exceed that of a Nimitz-class aircraft carrier, several billion dollars. Maintaining a secret fleet of Helicarriers would seriously stretch the budget of S.H.I.E.L.D. The value to the customer of surprise and versatility might also be provided by several smaller, lower cost vehicles, rather than a few, large, expensive craft.
SURF Research Seminar
Here is a video of a talk that I gave this summer to summer undergraduate research (SURF) students.
Turbulent Boundary Layer
Here are a few movies from a simulation of a turbulent boundary layer at supersonic Mach number (M = 2.25) and low Reynolds number (Reθi = 2000, δ+ = 560). The data correspond to case 3VW from Poggie, Bisek, and Gosse (Computers and Fluids, v. 120, 2015). Each case is a planar slice of the domain, and flow is from left to right. For the side-view movie, the field of view is 8δ x 2δ, and for all the plan-view movies, the field of view is 8δ x 8δ.
- Side view of density field
- Plan view of density field at y/δ = 0.80 (y+ = 452)
- Plan view of density field at y/δ = 0.16 (y+ = 93)
- Plan view of density field at y/δ = 0.02 (y+ = 13)
The dark regions in the density field correspond to hot, low-density, turbulent fluid near the wall. The lighter regions represents cold, high-density, irrotational freestream fluid. The dark δ-scale structures in the turbulence are traditionally called bulges, and the incursions of light, freestream fluid are called valleys. The interface between the light and dark regions is called the viscous superlayer; here turbulent and irrotational fluid meet. The turbulent boundary layer grows by capturing freestream fluid in the valleys, stretching and folding that fluid into thin sheets, and making it turbulent through viscous diffusion.
Poggie quoted by NOVA Next
NOVA Next is an online science magazine associated with the PBS NOVA television show. They have recently run a story on Plasma Aerodynamics that quotes me, Tom Corke, Subrata Roy, Steve Wilkinson, and others on the prospects for this field.
Update (Aug. 29): If you are interested in more information on this, there is an overview paper that I published with a group from AIAA in the ONERA AerospaceLab online journal. I published a shorter summary in Aerospace America (Nov. 2014, see pp. 10-12). Also of interest is a recording of a talk that I gave on the subject for Michigan Institute for Plasma Science and Engineering a couple of years ago.
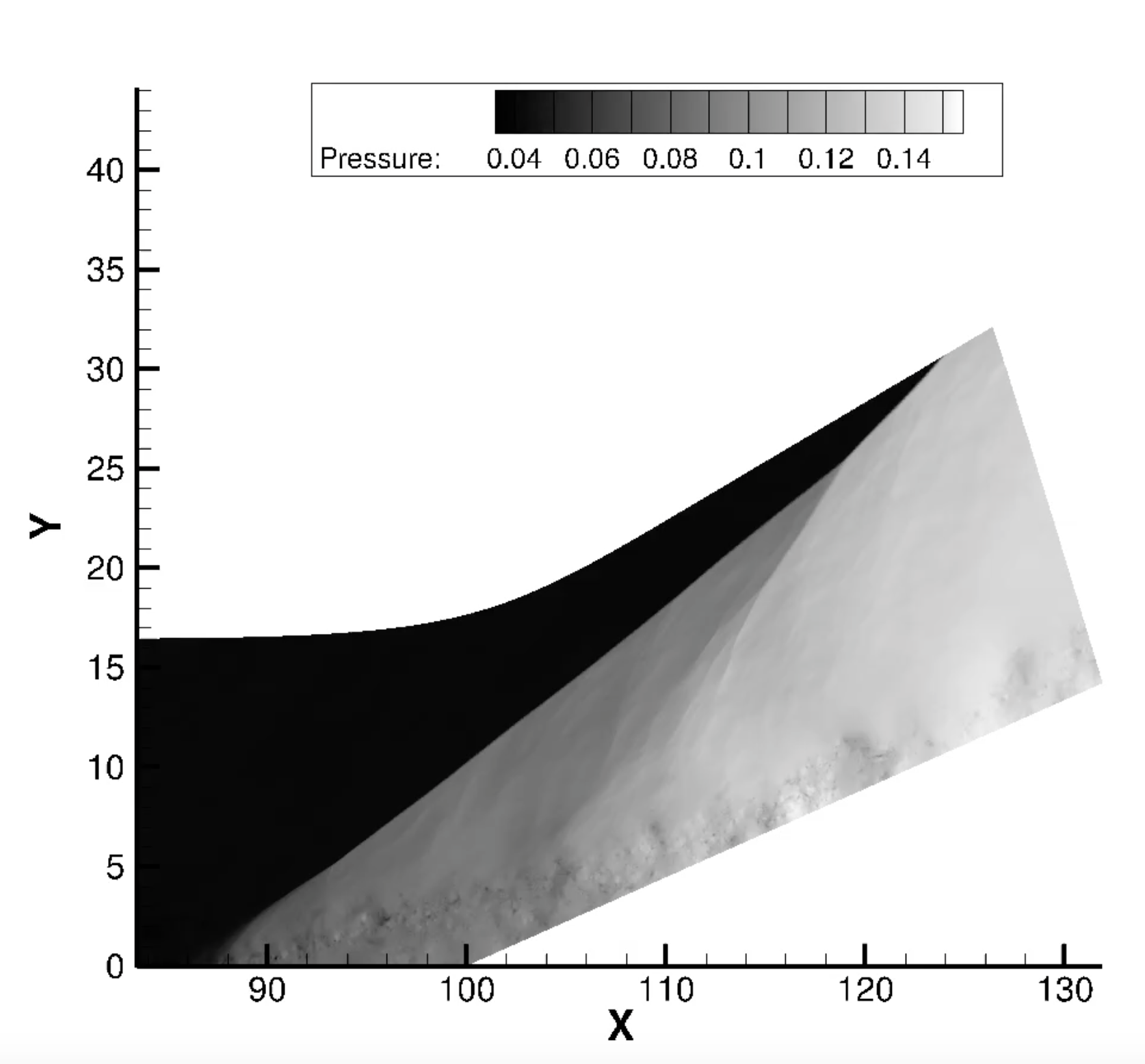
Mach 2.3 Turbulent Compression Ramp Flow
Mach 2.3 Turbulent Boundary Layer
Sample slice of the instantaneous density field in a Mach 2.3 turbulent boundary layer. The computational mesh for this direct numerical simulation was over 33 billion cells, and was run on up to 102400 cores under a DoD HPCMP Frontier Project. For full details of the computations, see Poggie et al., Computers & Fluids, v. 120, pp. 57-69, 2015.
About
Prof. Poggie's research interests have encompassed the experimental, computational, and theoretical aspects of fluid dynamics and plasma physics. Current work in our research group focuses on high Mach number flow, laminar-turbulent transition, large-scale separation unsteadiness, and electrical discharges for flow control.