Research at the interface of engineering and medicine

We develop new modeling and computer-based simulation techniques to address of problems in mechanical and biomedical engineering. We specialize on interface problems. These include classical interfacial mechanics and problems at the interface of engineering and medicine. Particular research interests include Computational Mechanics, Phase-field Methods, Biomechanics, Tumor-growth modeling, and Multiphase Flow.

A complete publication list and citation data may be found at Google Scholar

Selected recent publications

1. T. Hu, H. Wang, H. Gomez, Direct van der Waals simulation (DVS) of phase-transforming fluids, Science Advances, 9, eadg3007, 2023.
2. H. Gomez, Y. Leng, T. Hu, S. Mukherjee, V. Calo, Phase-Field Modeling for Flow Simulation, Frontiers in Computational Fluid-Structure Interaction and Flow Simulation, 79-117, 2023.
3. G. Lorenzo, N. di Muzio, C. Deantoni, C. Cozzarini, A. Fodor, A. Briganti, F. Montorsi, V. Perez-Garcia, H. Gomez, A. Reali, Patient-specific forecasting of postradiotherapy prostate-specific antigen kinetics enables early prediction of biochemical relapse, Iscience, 25, 2022.
4. S. Bhopalam, J. Bueno, H. Gomez, Elasto-capillary fluid-structure interaction with compound droplets, Computer Methods in Applied Mechanics and Engineering, 400, 115507, 2022.
5. Y. Leng, P. Vlachos, R. Juanes, H. Gomez, Cavitation in a soft porous material, PNAS nexus, 1, pgac150, 2022.
6. A. Moure, G. Vilanova, H. Gomez, Inverting angiogenesis with interstitial flow and chemokine matrix-binding affinity, Scientific reports, 12, 4237, 2022.
7. A. Moure, H. Gomez, Phase-field modeling of individual and collective cell migration, Archives of Computational Methods in Engineering, 28, 311-344, 2021.
8. G. Lorenzo, Thomas J.R. Hughes, P. Dominguez-Frojan, A. Reali, H. Gomez, Computer simulations suggest that prostate enlargement due to benign prostatic hyperplasia mechanically impedes prostate cancer growth, Proceedings of the National Academy of Sciences, 116(4), 1152-1161, 2019

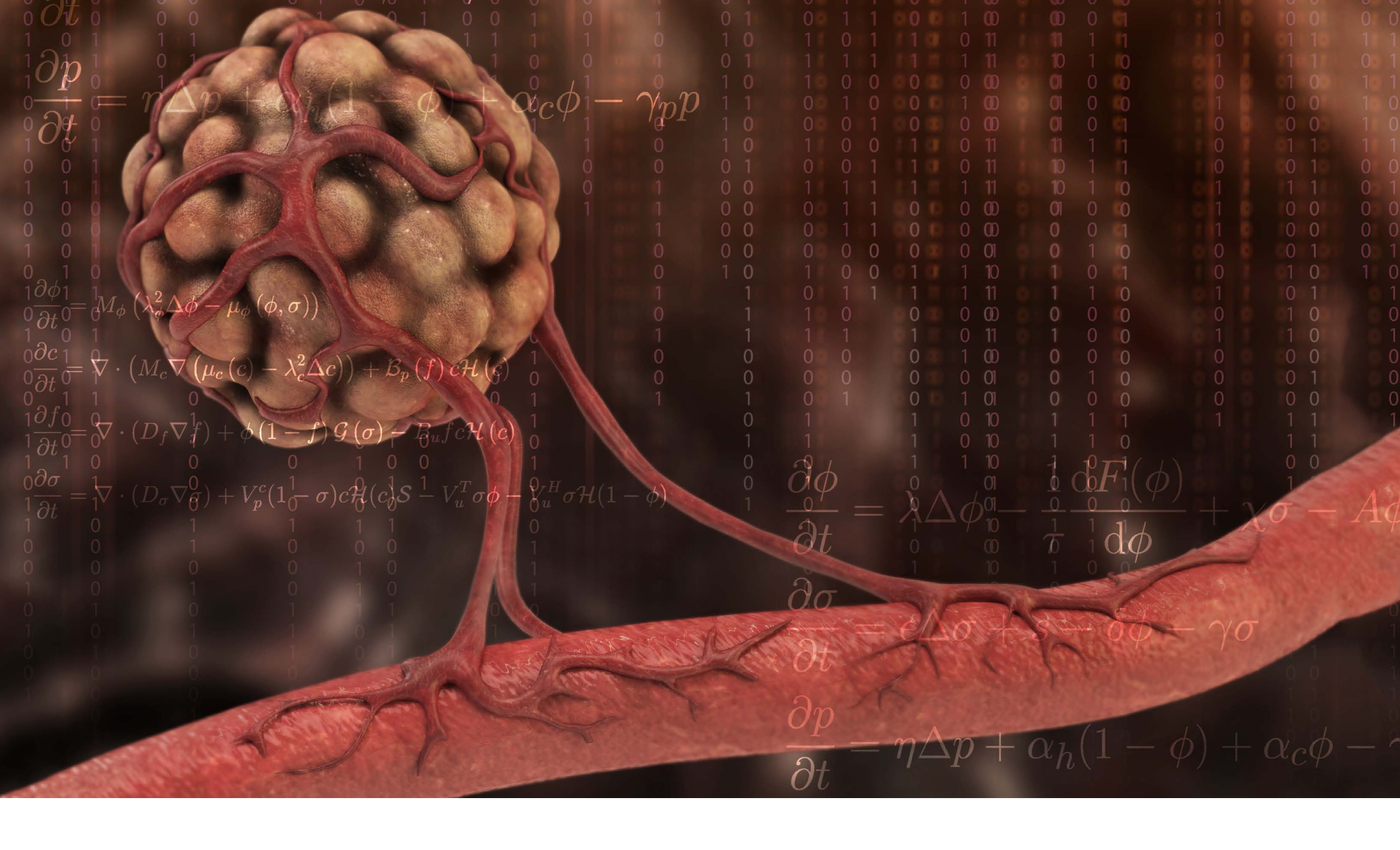
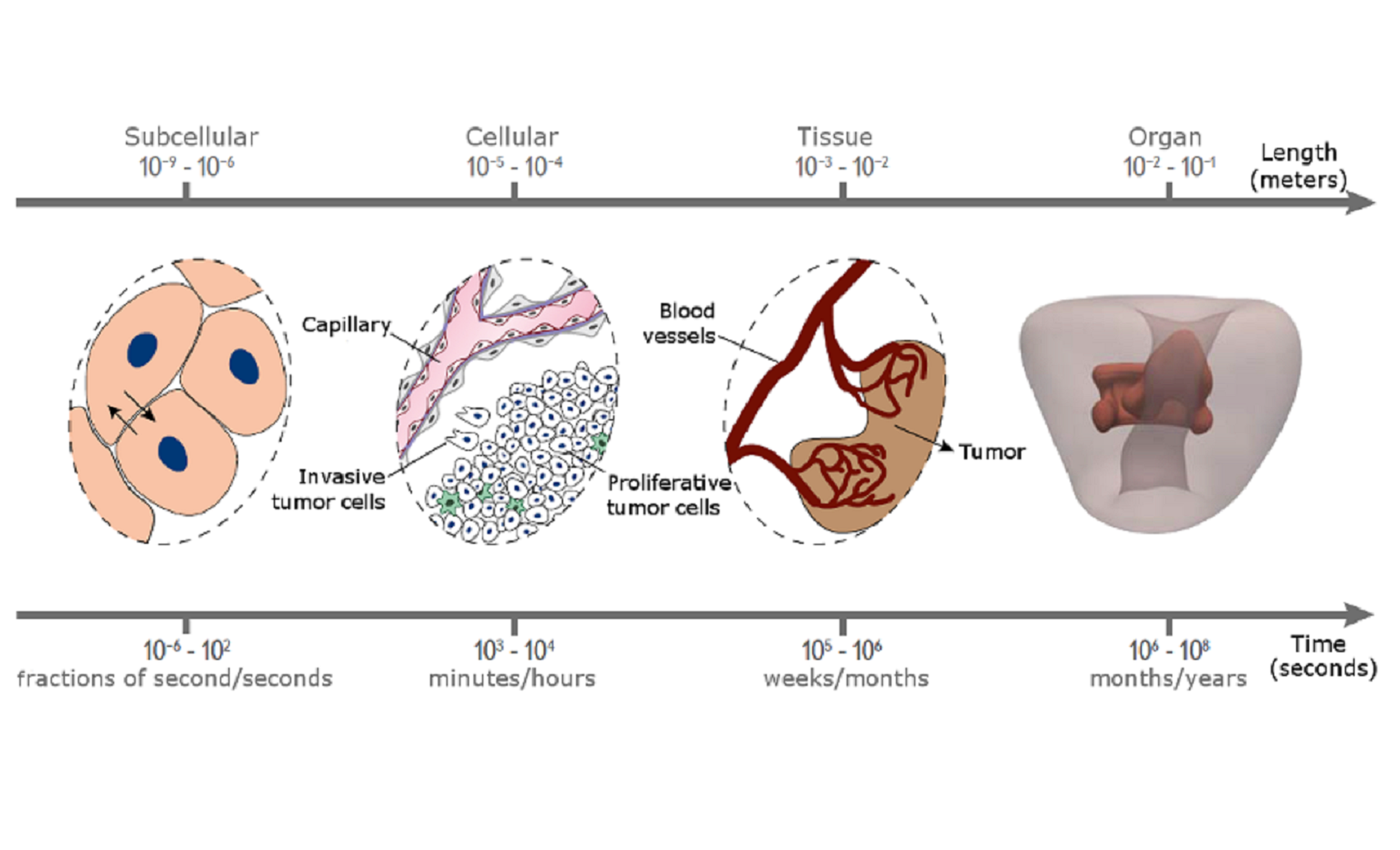
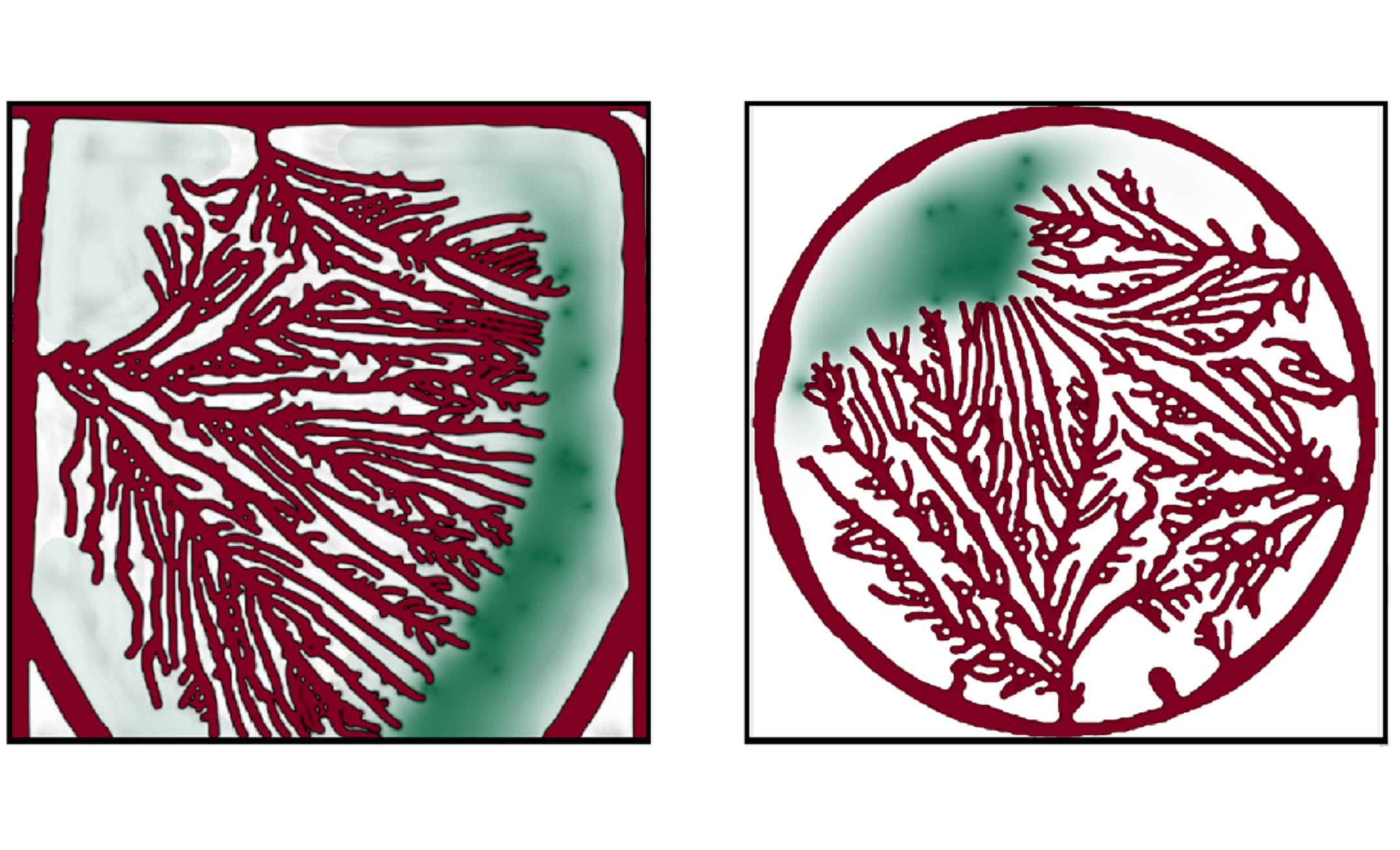
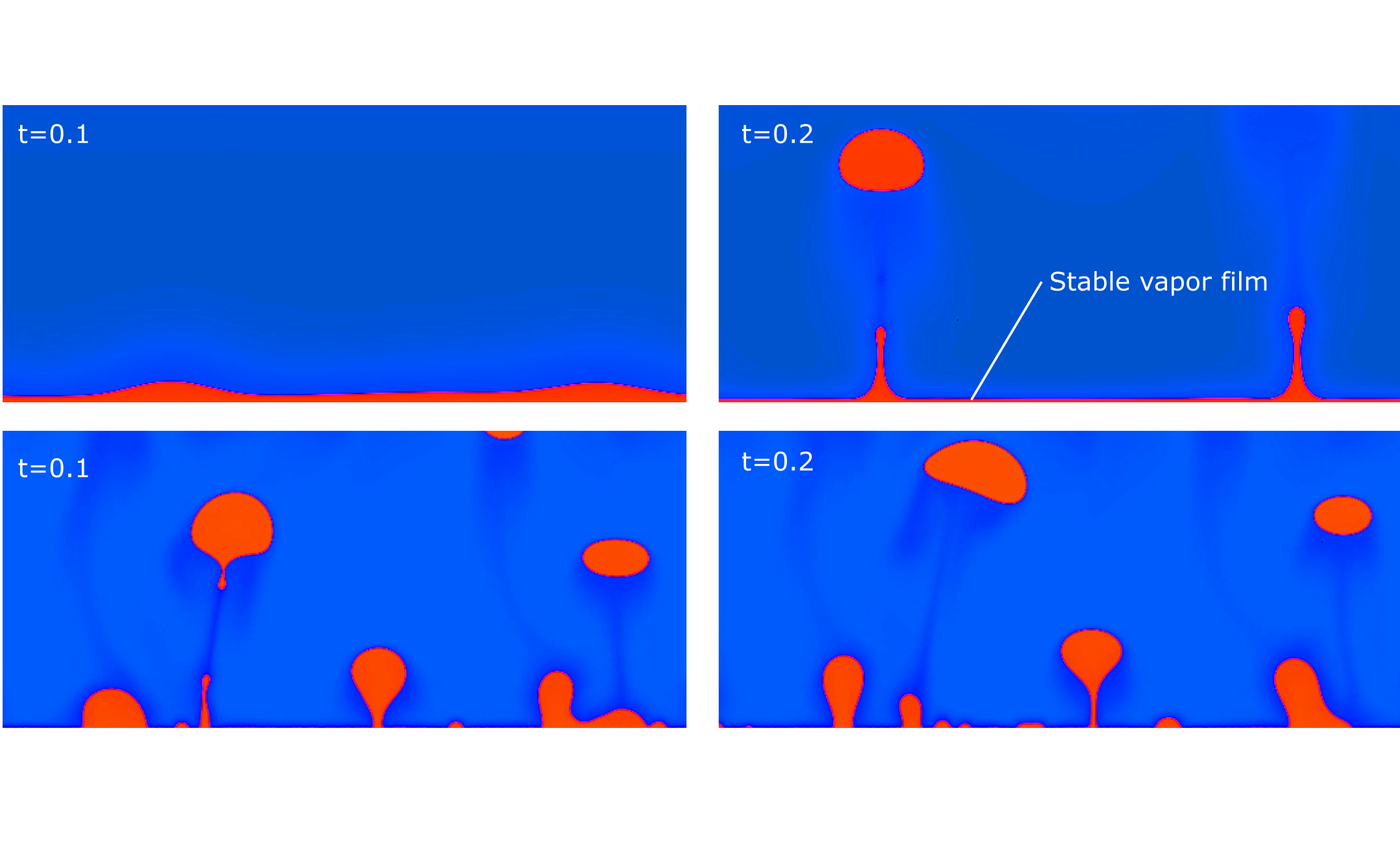
   Featured in EurekAlert!, Medical Xpress, Futurity, JNCCN 360

9. A. Moure, H. Gomez, Three-dimensional simulation of obstacle-mediated chemotaxis, Biomechanics and Modeling in Mechanobiology, 17(5), 1243-1268, 2018
10. H. Casquero, Y.J. Zhang, C. Bona-Casas, L. Dalcin, H. Gomez, Non-body fitted fluid-structure interaction: Divergence-conforming B-splines, fully-implicit dynamics, and variational formulation, Journal of Computational Physics, 374, 625-653, 2018.
11. J. Bueno, Y. Bazilevs, R. Juanes, H. Gomez, Wettability control of droplet durotaxis, Soft Matter, 14, 1417, 2018.
12. G. Lorenzo, M. Scott, K. Tew, T.J.R. Hughes, Y.J. Zhang, L. Liu, G. Vilanova, H. Gomez, Tissue-scale, personalized modeling and simulation of prostate cancer growth, Proceedings of the National Academy of Sciences, 113(48), E7663-E7671, 2016.

    Featured in Nature Reviews Urology, Science Daily, Medical Xpress, Prostate Cancer News Today

Recent News

• 11/2023 - Mario de Lucio receives the Hillberry Award. Congratulations!
• 11/2023 - Hector Gomez receives the Acorn Award.
• 12/2023 - We have just published a chapter in Frontiers in Computational Fluid-Structure Interaction and Flow Simulation. Research from Lead Investigators under Forty.
• 07/2023 - Hector Gomez receives the Fellow Award from USACM.
• 06/2023 - Mario de Lucio selected as runner up in the poster competition at the EMI Conference. Congratulations!
• 05/2023 - Hector Gomez appointed University Faculty Scholar.
• 05/2023 - Saikat Mukherjee successfully defended his PhD Thesis. Congratulations!
• 08/2022 - Hector Gomez appointed Perry Scholar of Academic Excellence.
• 04/2021 - Hector Gomez appointed Editor of Engineering with Computers.
• 09/2019 - Adrian Moure receives the Outstanding PhD Thesis Award ! This is the third award that he receives for his PhD Thesis. Well done !
• 11/2018 - We have just published a chapter in Frontiers in Computational Fluid-Structure Interaction and Flow Simulation. Research from Lead Investigators under Forty
• 09/2018 - Hugo Casquero receives the "Extraordinary PhD Thesis Award" for his work on immersed, isogeometric methods for fluid-strcuture interaction
• 09/2018 - Jesus Bueno receives the "Extraordinary PhD Thesis Award" for his work on interaction of soft solids and multiphase flows
• 03/2018 - Adrian Moure receives the "PhD Thesis Award" from both SEMNI and SEMA !
• 07/2017 - Hector Gomez receives the Gallagher Young Investigator Award from the US Association for Computational Mechanics
• 06/2017 - Hector Gomez receives the Princess of Girona Scientific Research Award (for Spanish or Spain researchers under age 36 in all fields of science, engineering anh humanities). See below when Hector received the award from the Kings of Spain