Developing efficient and accurate computational methods for solving coupled multi-physics problems is the primary goal of my research. The disparity in the length and time scales usually involved in these problems makes them extremely challenging. Researchers have devoted significant effort to address the coupling of multi-physics phenomena in space through techniques such as domain decomposition and multi-scale methods but a commensurate effort to couple multiple scales in time is lacking in the current literature.
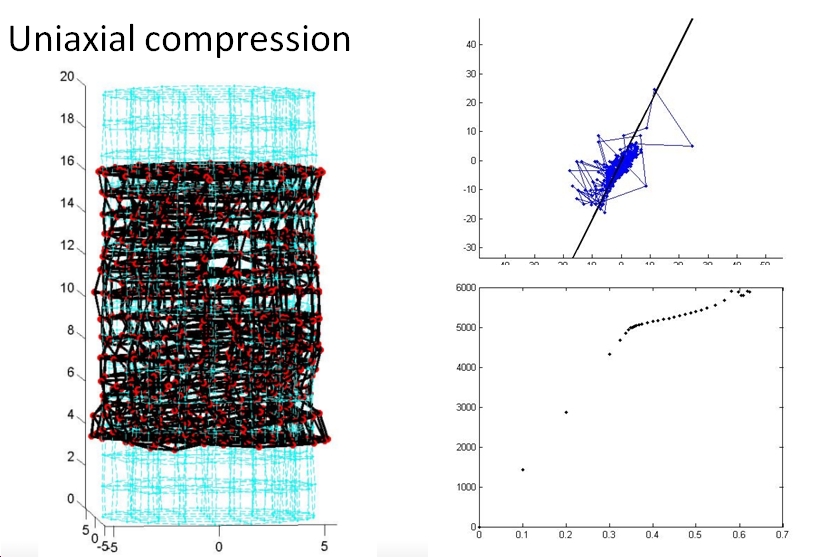
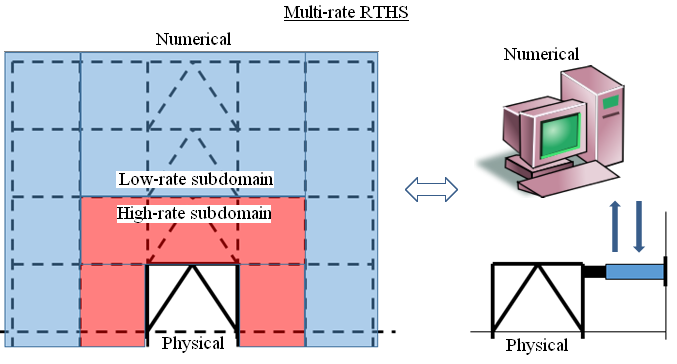
Consider the problem of coupling multiple time scales for non-linear dynamic analysis of large structures with complex geometries efficiently. Such problems have been solved, in the past, by discretizing the structural domain in space with finite elements and using a time-stepping scheme for numerical time integration. However, using a uniform time step for the entire mesh that meets that stability and accuracy requirements of all the elements is computationally very inefficient.
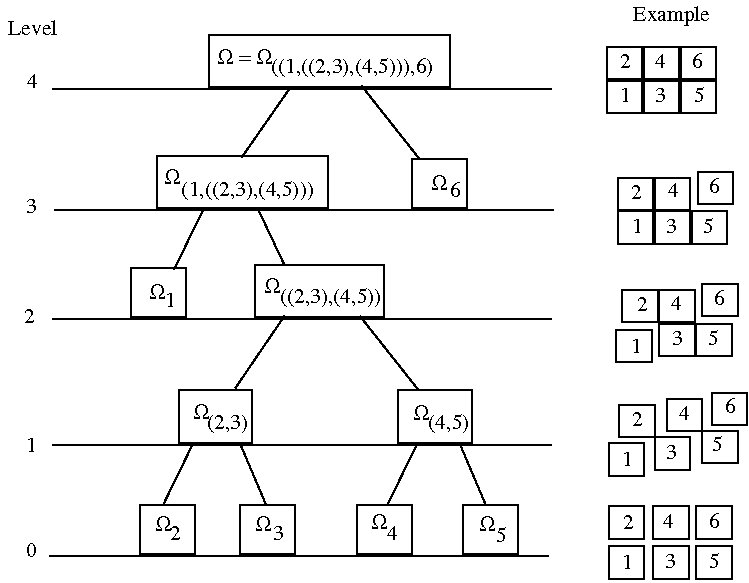
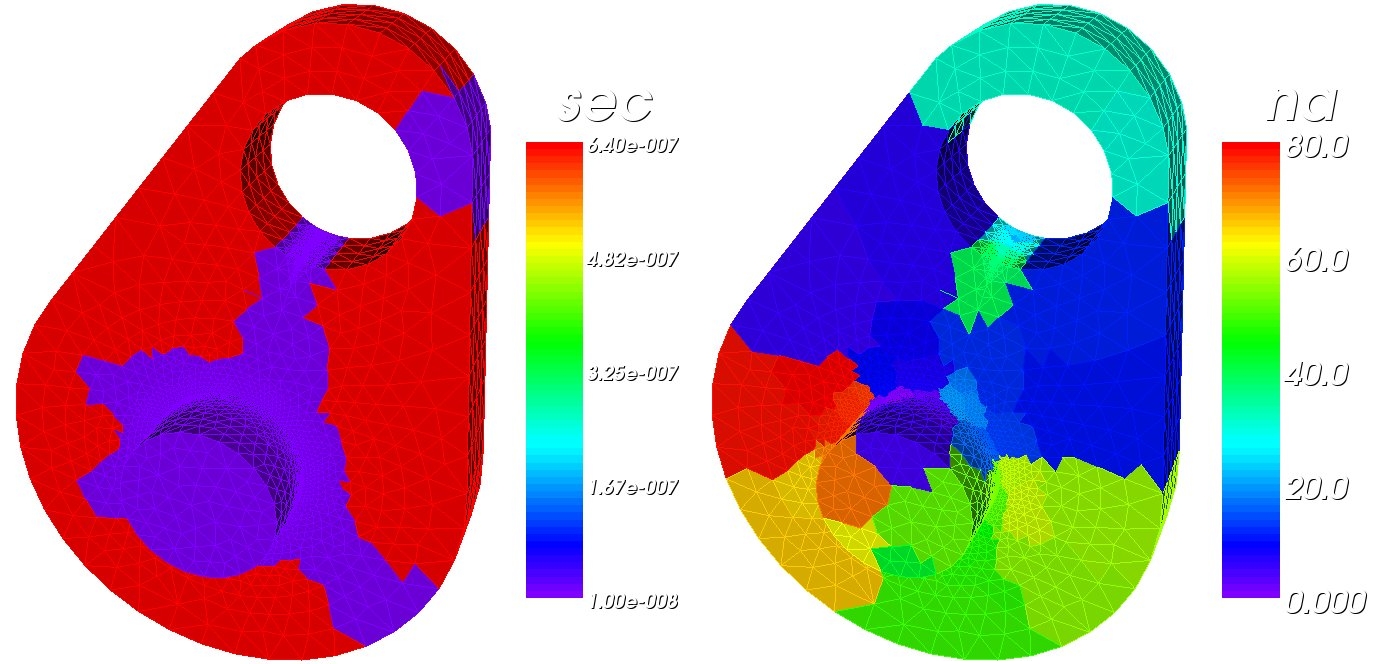
The present multi-time-step coupling method is based on a dual Schur domain decomposition method (FETI: finite element tearing and interconnecting) that uses Lagrange multipliers to enforce the continuity of the solution across the interfaces between the subdomains. The subdomains can be integrated with different time steps and/or time stepping schemes. The method has been shown to be unconditionally stable, energy preserving and computationally very efficient. The multi-time-step method has also been extended for problems with geometric and material non-linearities. Multiple subdomains with multiple levels of time steps are coupled using a hierarchical recursive coupling method. An efficient parallelization based on message passing interface (MPI) that uses a recursive tree topology for distributing subdomains between processors has also been developed.
Animations:
Axial Stress wave in Notched Beam
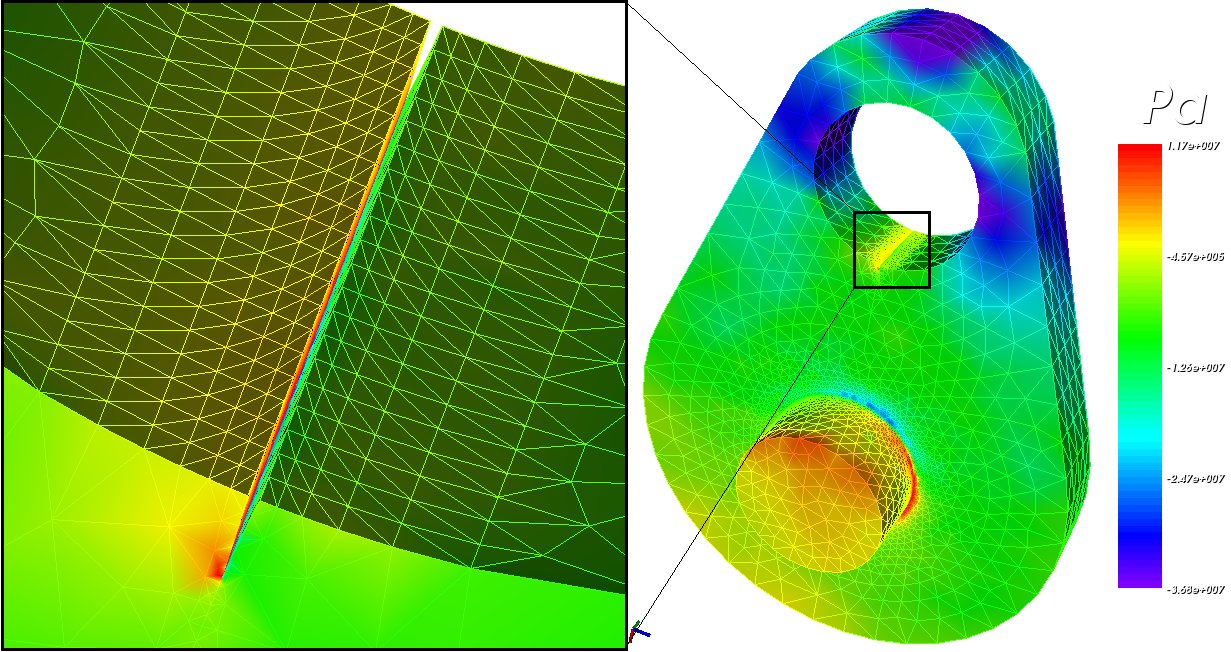
Rocket case with cracks subject to sudden head end pressure
Recursive domain decomposition and coupling of large finite element models