Learning-based multiscale modeling

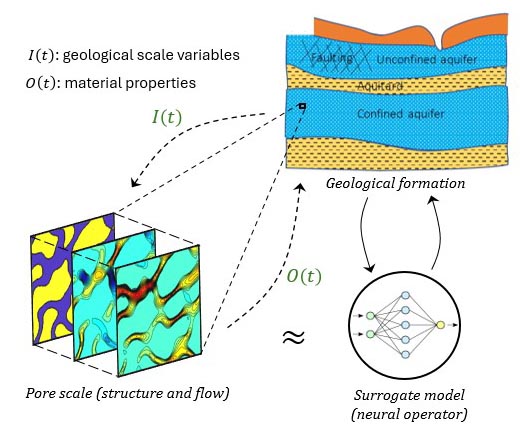Multiscale methods bridge the gap between finer and coarser scales by providing closure relations and passing information across scales. However, traditional concurrent multiscale (FE²) methods require repeatedly solving the problem at individual scales, which is computationally expensive. We develop surrogate models that serve as closure relations by learning the underlying physics of the lower scale using neural networks. This approach results in learning-based multiscale methods that provide the accuracy of concurrent multiscale methods at a cost comparable to traditional constitutive relations. We apply this framework to fluid transport in permeable geological formations, where fluid reacts with the medium, changing morphology and transport properties, and creating a complex multiscale problem. Reactive transport is important for CO₂ sequestration, geothermal energy, and hydrogen storage, and is essential for advancing these technologies.

Inverse problems and uncertainty quantification

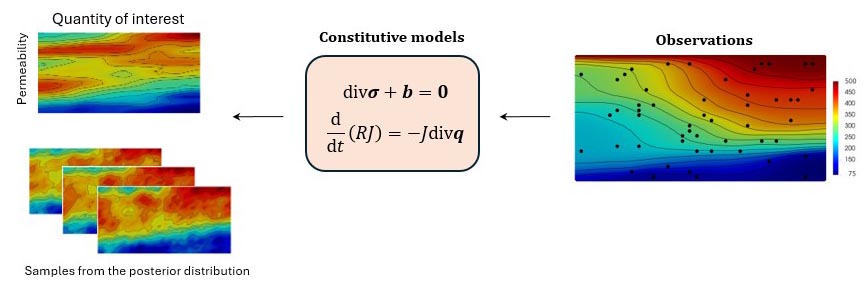Many engineering problems can be studied as inverse problems, where we use mathematical models to infer unknown parameters (i.e., material properties, initial and boundary conditions) from often noisy experimental or field observations. We use Bayesian inversion frameworks to integrate physical models with data, identify uncertain model parameters, and quantify their uncertainties. We focus on high-dimensional engineering problems, particularly in settings where data is noisy or incomplete.

Energetic models 

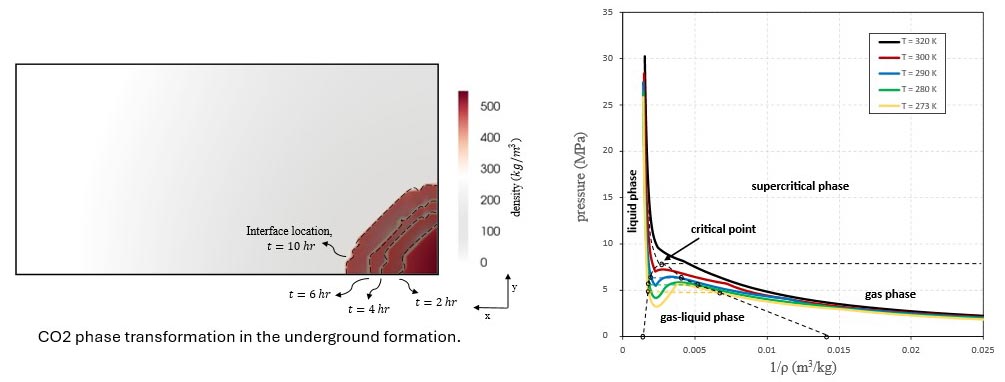We study variational energetic formulations for poroelasticity. This approach begins from the total free energy density of the system, and the governing equations are derived by minimizing the corresponding energy functional, which provides a robust framework. We particularly focus on applying these methods to complex multi-physics systems, including multiphase flow, phase transitions, and large deformations.

Accelerated micromechanical modeling

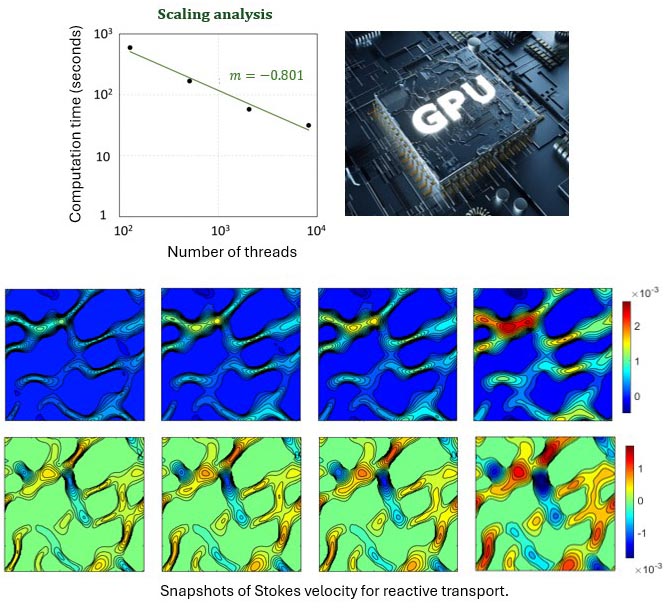High-fidelity micromechanical models are essential for understanding the underlying physics of underground processes and microscopic interactions between different phases. They are also important for generating rich databases to serve as a foundation for advancing data-driven modeling approaches. We develop accelerated micromechanical models that leverage parallel computing algorithms, enabling implementation on GPU accelerators to provide scalable and portable solutions for the partial differential equations governing microscopic underground processes.