Lanczos Benchmark Details on Recompute Hamiltonian (June / July 2007)
NEMO 3-D was benchmarked on a broad range of HPC platforms in June and July 2007. 5 of the 6 benchmark platforms were ranked on the TOP500 list of June 2007. The benchmark machines are:
-
#2, ORNL, Jaguar, Cray XT3/4, with 23016 cores, 2GB RAM/core
-
#7, RPI, eServer Blue Gene Solution, IBM B/G, with 32768 cores, 256MB RAM/core
-
#8, NCSA, Abe, XeonQ (Quad core, dual socket), with 9600 cores, 1GB RAM/core
-
#30, IUPU, Big Red, IBM JS21, with 3072 cores, 2GB RAM/core
-
#46, PSC, Big Ben, Cray XT3, with 4136 cores, 1GB RAM/core
-
unranked, Purdue, XeonD (Dual core, dual socket), with 672 cores, 2GB/4GB RAM/core
The benchmark constitutes 500 Lanczos iterations. These iterations include the communication needed to construct the reduced order tridiagonal Lanczos matrix.
NEMO 3-D can either store the Hamiltonian matrix or recompute it on the fly for use in the matrix multiply. Recomputing the matrix at every multiply step is computationally intensive, however it reduces the memory footprint and enables running on CPU-rich, memory poor machines. This page shows the benchmark where the matrix elements are recomputed / reconstructed on the fly on every matrix-vecotr multiply step. The equivalent stored matrix benchmarks are shown
below. All machines are compared on a single graph on a different page.
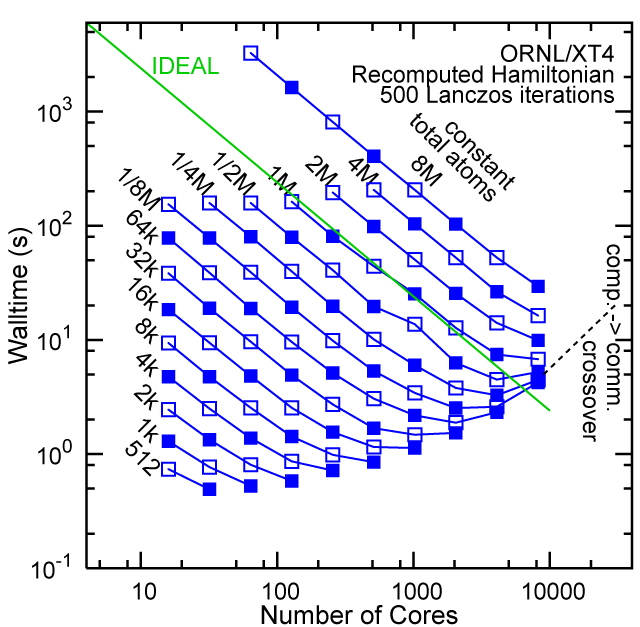
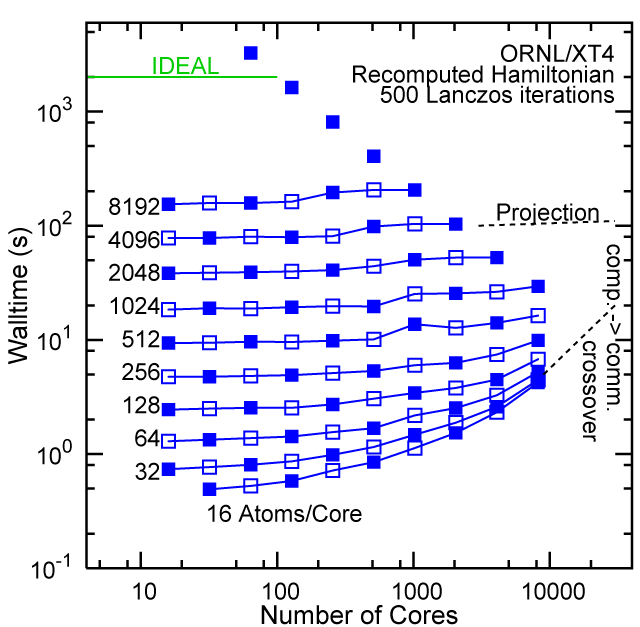
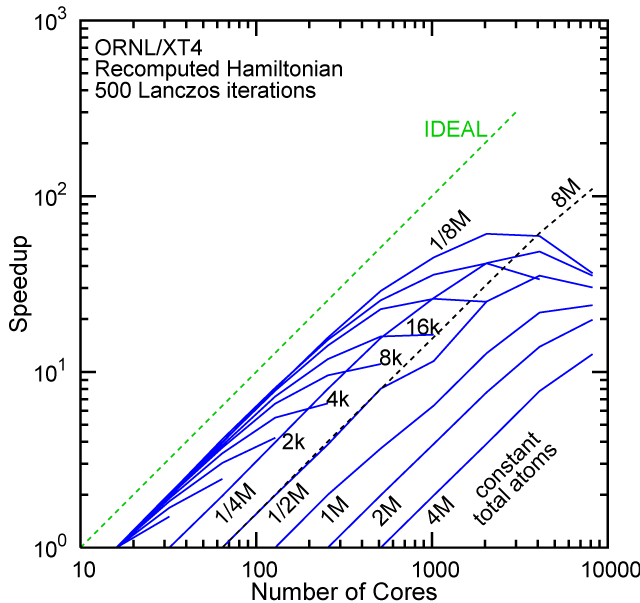
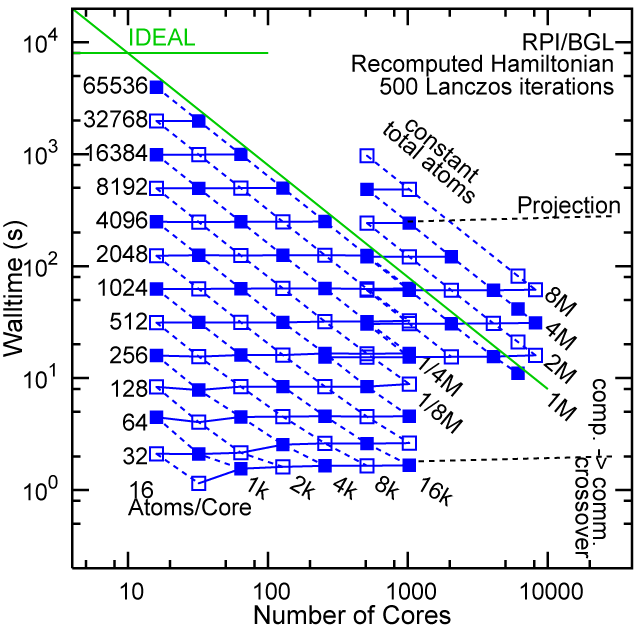
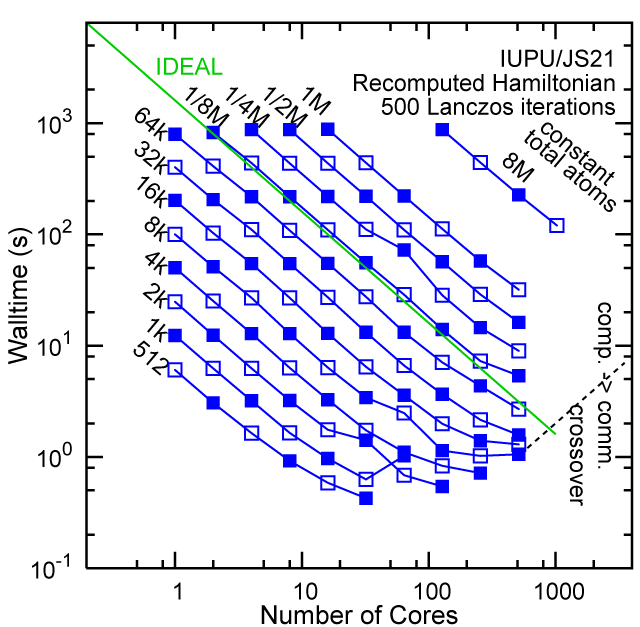
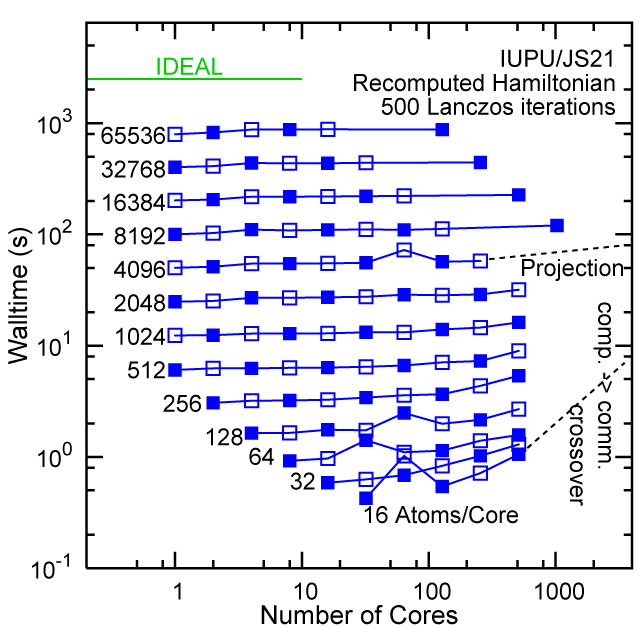
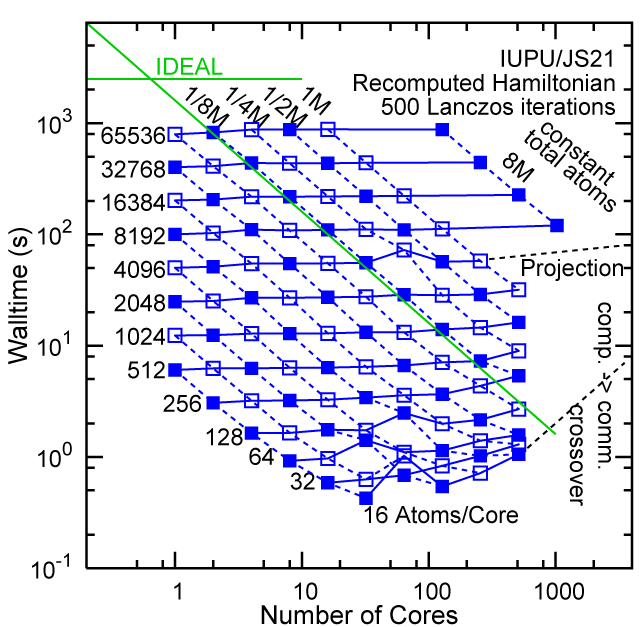
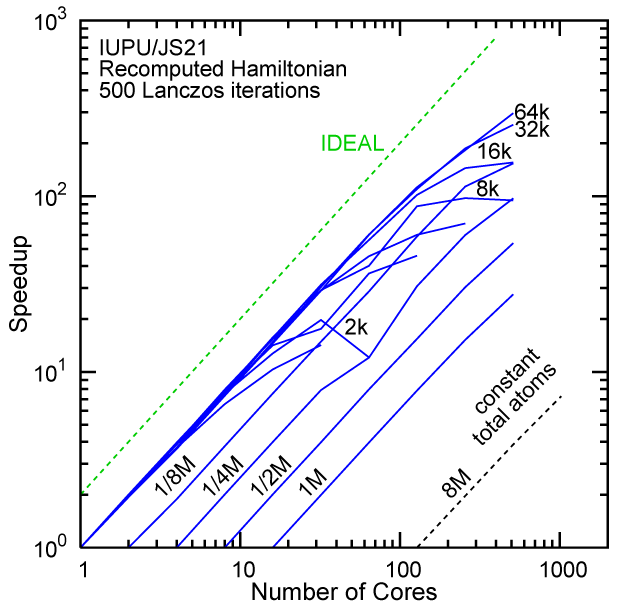
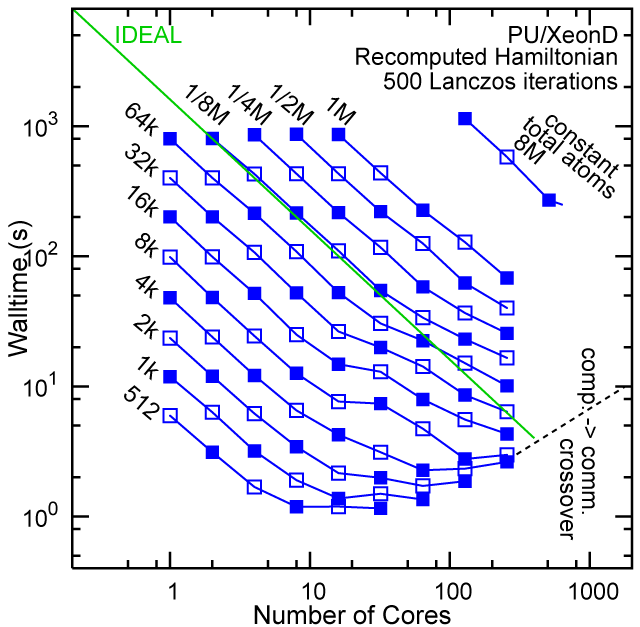
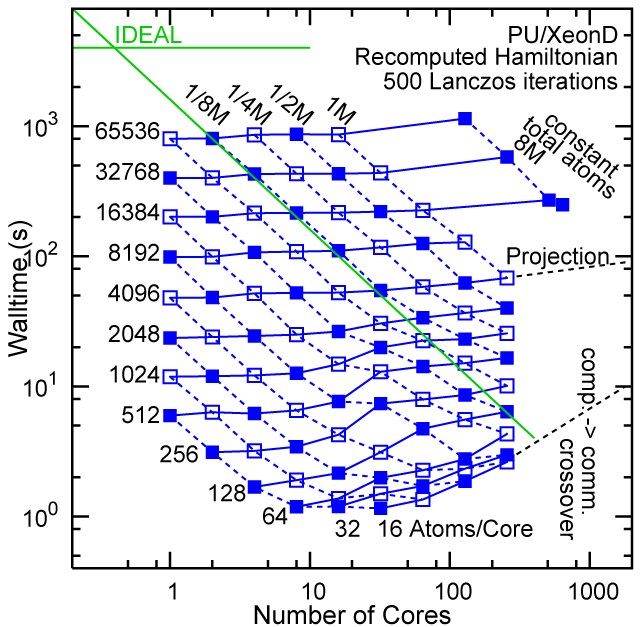
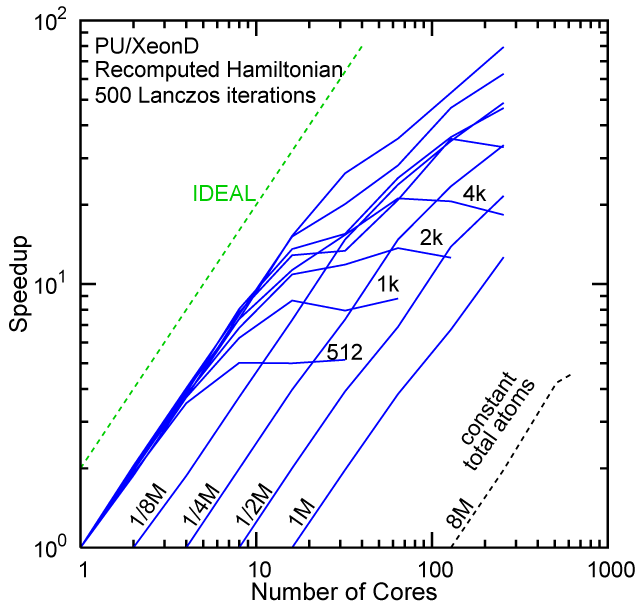
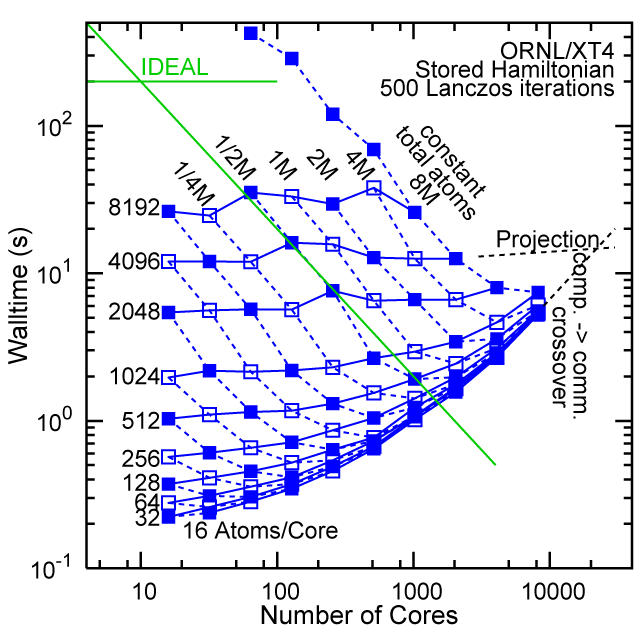
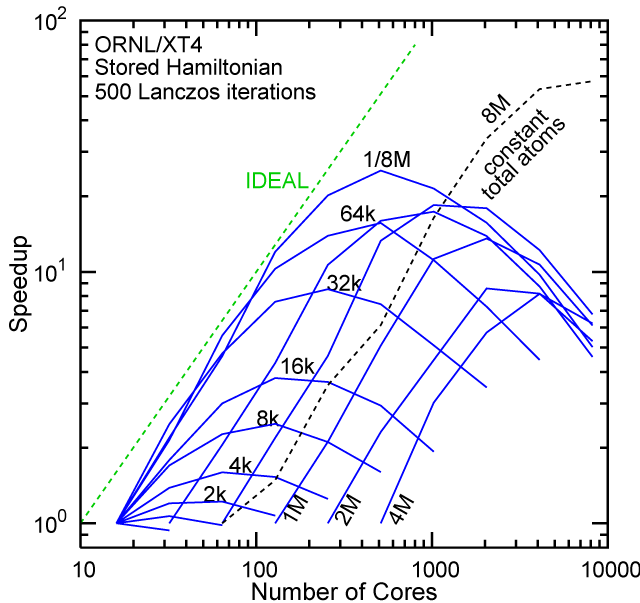
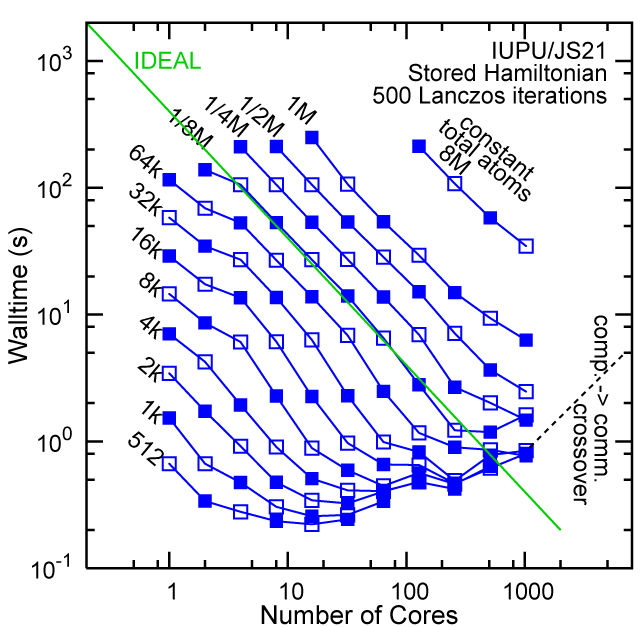
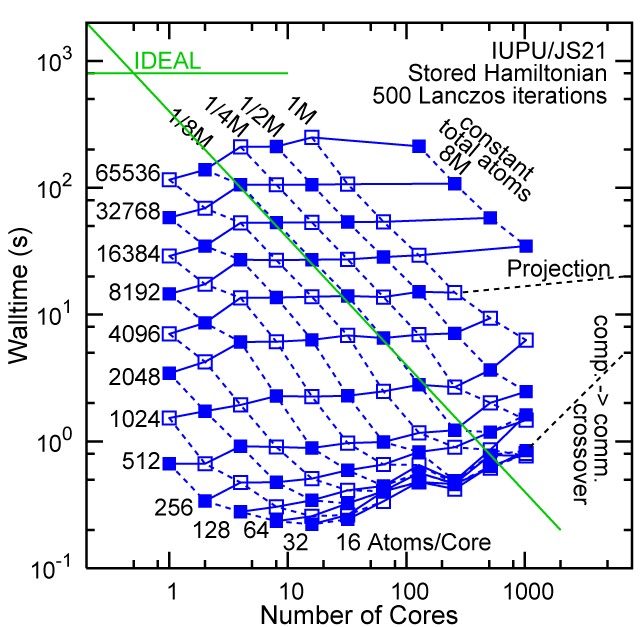
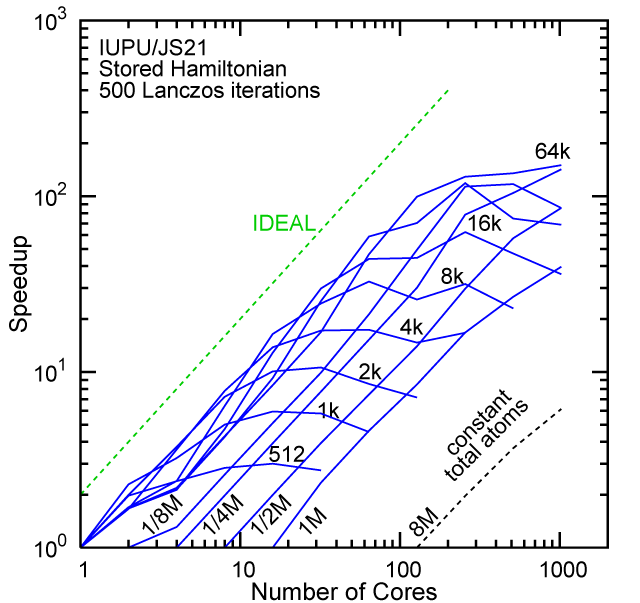
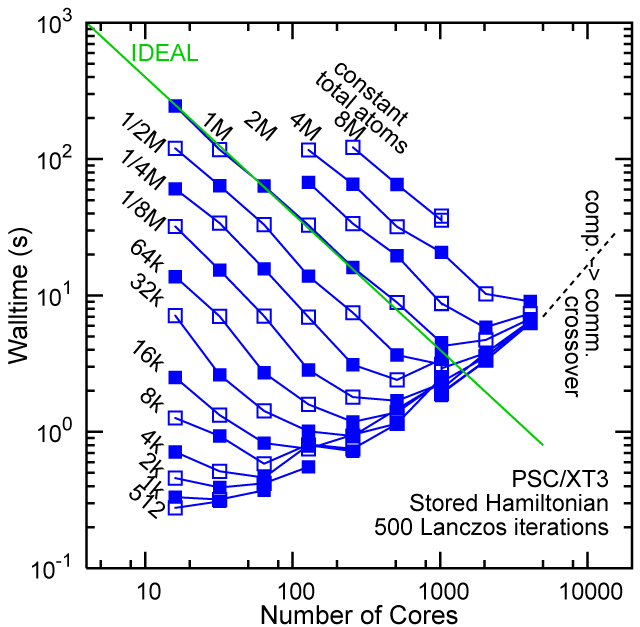
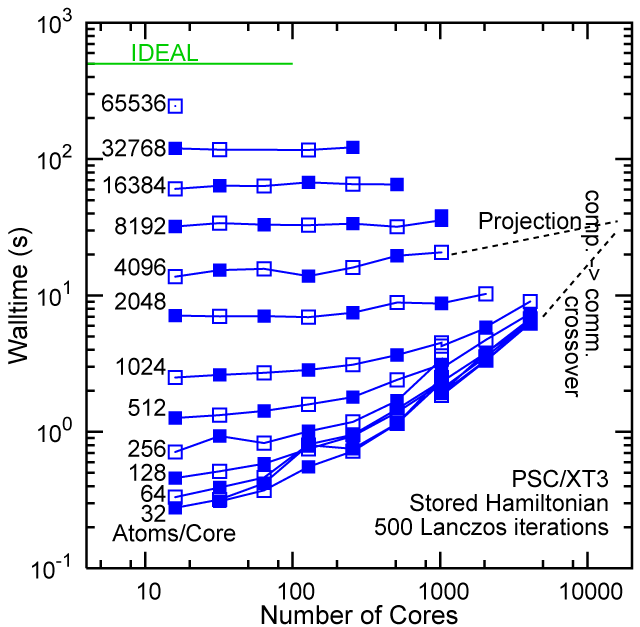
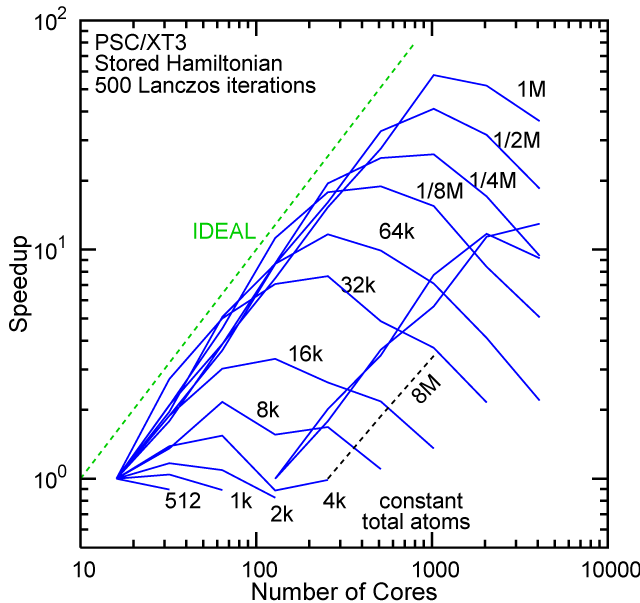
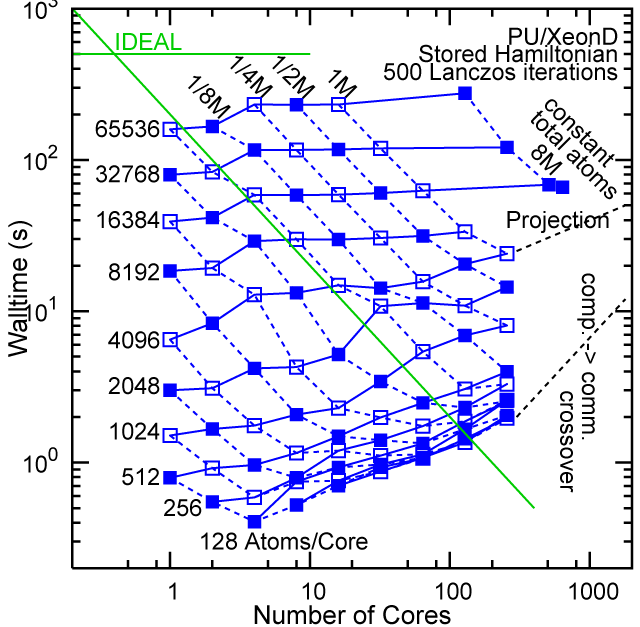
Each row contains the scaling data for a particular machine. The first column shows the stron scaling representation, where the total problem size is held constant and the number of cores is increased. Ideal behavior is represented by a diagonal line on a log-log scale. The second column represents the weak scaling data where the number of atoms per core is held constant and the the number of cores and the total prblem size is increased. Here a horizontal flat line would be the ideal scaling result. The third colum represents the combined data in column one and two. The fourth column shows the strong scaling linear speed-up curves for a constant problem size normalized to the data point at the lowest core count. The 8 million atom line is shown special as a dashed line, as that benchmark is the critical comparison for all platforms.
|
#2/TOP500, Recompute Lanczos Benchmark.
#7/TOP500, Recompute Lanczos Benchmark.
#30/TOP500, Recompute Lanczos Benchmark.
Purdue Pete, Recompute Lanczos Benchmark.
Lanczos Benchmark Details on Stored Hamiltonian (June / July 2007)
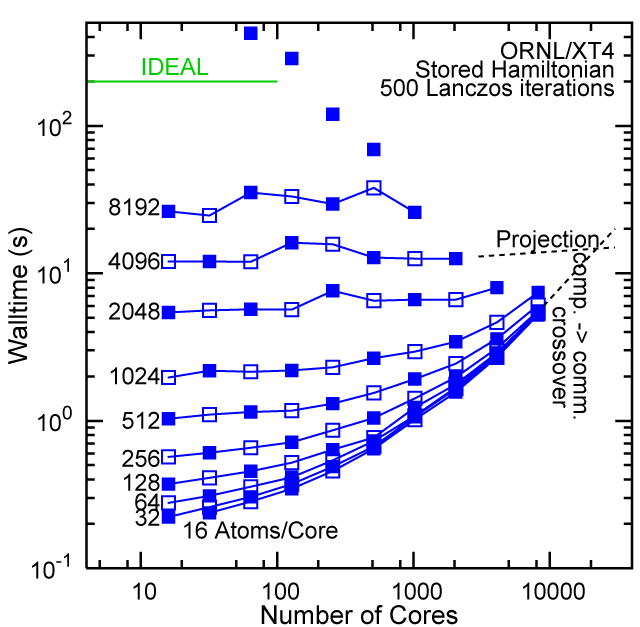
When the Hamiltonian is stored, significantly more memory is needed to execute the code per core. If the bandwidth of the memory bus is fast enough, the stored matrix can be brought into the core fast enough even on multi-core CPUs. This results in a significant reduction in the compute time, as the matrix element construction is non trivial and takes about a factor 4-5x of the computation of the matrix-vector computation itself. The speed-up due to storing the matrix turns into an immediate speed-up of the code. As the computational need per atom is reduced by a factor of 4-5x, the computation to communication ratio becomes less favorable and good scaling to a large number of cores is only achieved for large problem sizes. The benchmarks below seem to indicate that the sweet spot is around 4,096 atoms per core. At that atom count (and above) excellent scaling can be expected on all the high-end platforms tested here.
#2/TOP500, Store Lanczos Benchmark.
#30/TOP500, Store Lanczos Benchmark.
#46/TOP500, Store Lanczos Benchmark.
Purdue Pete, Lanczos Benchmark.
-->