A short presentation (Nov. 16, 2021): PDF Version PPTX Version
Working with Sorin Matei and Robert Kirchubel within the Purdue FORCES Initiative, our team has been developing an alternative approach to modeling battles and civilian crises. In conventional wargames, units are described as discrete agents, essentially game pieces. This involves a rather arbitrary aggregation of complex groups. Our approach is to treat units with a continuous flow, or probabilistic, model. This approach can potentially provide a more realistic portrayal of group motion, and describe the location of discrete objects in terms of a probability density. With this perspective, we hope to provide decision makers with more intuitive understanding of the momentum of conflict and provide a useful tool for training and decision making.
A description of a preliminary version of the Battle Flow Model was published in J. Poggie, S. Matei, and R. Kirchubel, "Simulating Military Conflict with a Continuous Flow Model," Journal of the Operational Research Society, DOI: 10.1080/01605682.2020.1825017. Our paper on Pickett's Charge is: J. Poggie, S. Matei, and R. Kirchubel, "Continuous Flow Model of a Historical Battle: A Fresh Look at Pickett's Charge," DOI: 10.48550/arXiv.2203.11035.
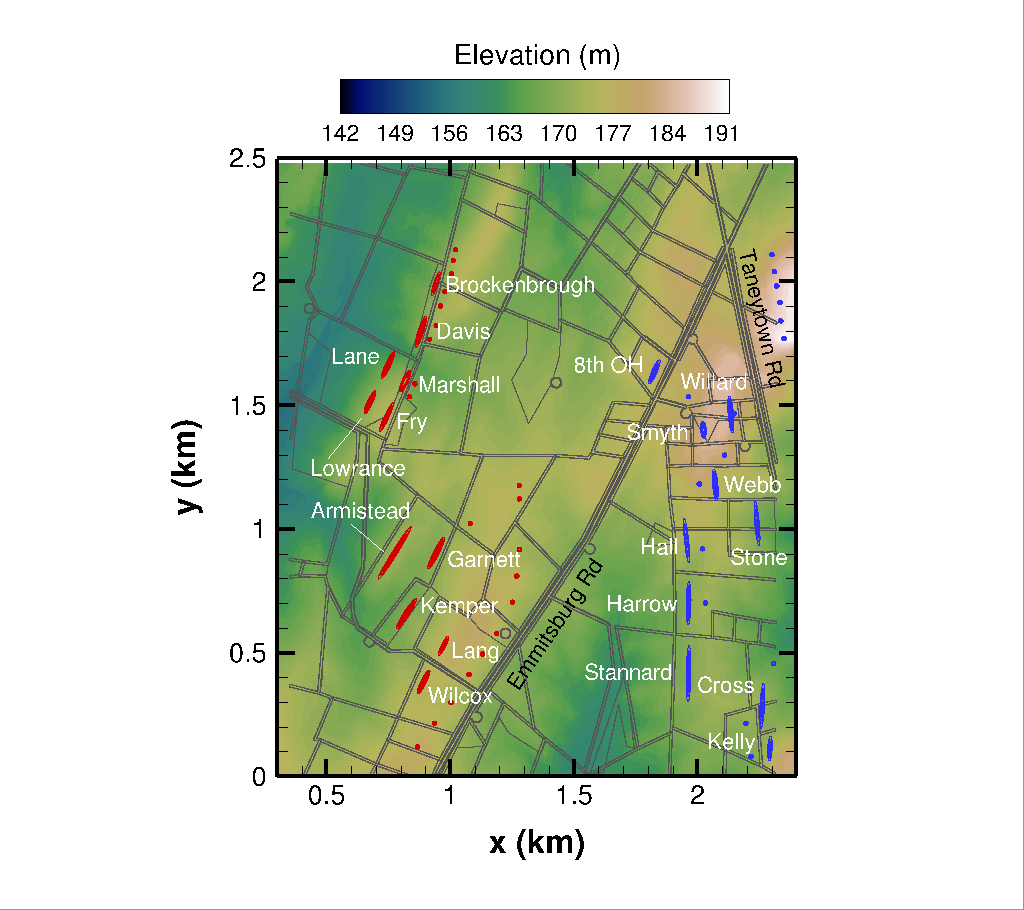
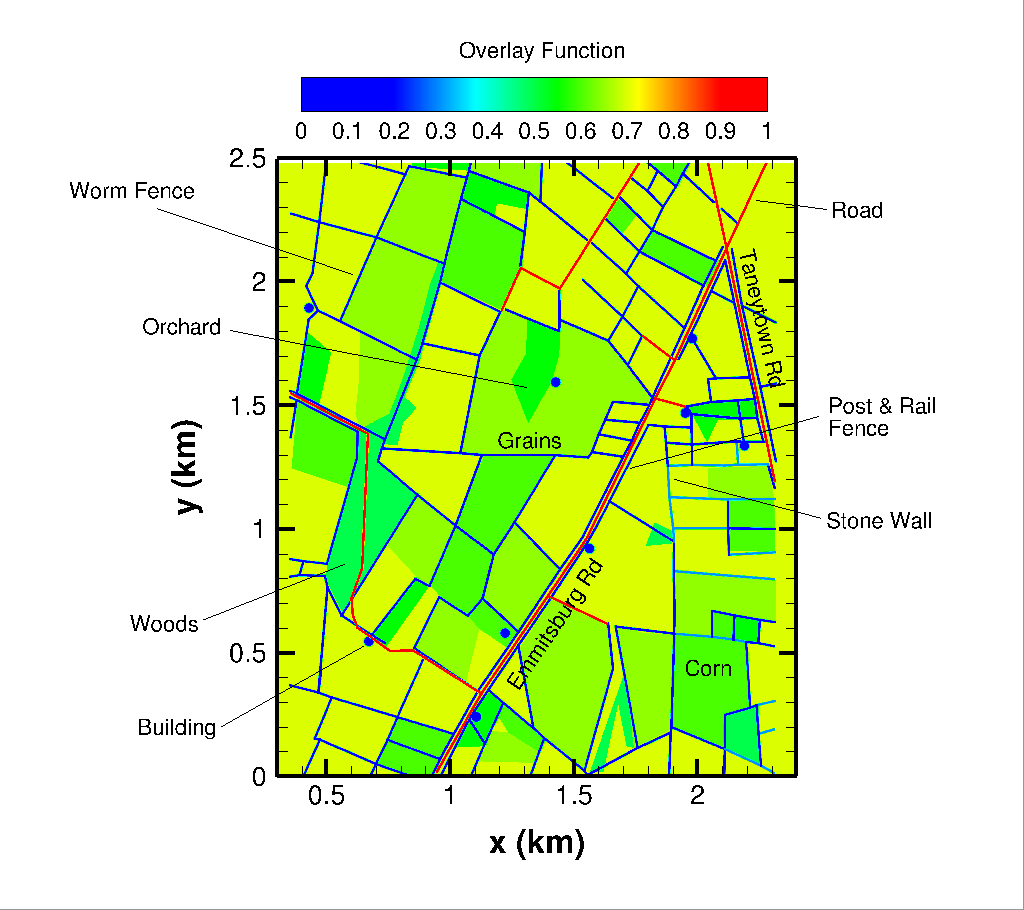
Here we show the results of initial simulations of the Battle of Gettysburg, specifically Pickett's Charge on the afternoon of July 3, 1863. The figure at left below shows the initial conditions at the brigade level of aggregation, a labeled version of the first frame in one of the movies below. The color scale in the background gives the local elevation. The gray lines represent an overlay layer describing terrain type, including roads, walls, fences, and vegetation. The intersection of Emmitsburg Road and Taneytown Road forms an X at the upper right. The color contour lines represent troop density, or probability of finding a soldier in a given location, with red for Confederate and blue for Union troops. Blue and red dots indicate the locations of groups of artillery pieces. At right below is a detailed presentation of the overlay layer. (Many thanks to graduate student Matthew Ellis and undergraduate Collin Tofts for helping to reconstruct the historical map.)
Movies of preliminary simulations are presented below. The videos below show results the an army level of aggregation. The first video shows the simulation with full details, whereas the second omits the effect of elevation and terrain features.
As might be expected, the terrain effects are seen to produce wrinkling of the unit density contours that is not present for the perfectly flat terrain case. A more striking result is that the Union forces take extra casualties, and the Confederates fewer, under the conditions of perfectly flat terrain. The terrain effects slow the pace of battle, and they favor the defenders. The slow progress of the Confederate troops toward the Union lines exposes the attacking Confederates to heavy ranged fire for an extended period.
Movies of simulations at to the brigade level are presented next. The first video shows a simulation with our Battle Flow model, whereas the second shows a similar simulation with a conventional, discrete agent model.
In the first (continuous flow) simulation, the Confederate troops initially march toward the Union lines, with their formation disrupted by the various fences and other obstacles on the field of battle. The fences on either side of Emmitsburg Road form a particularly difficult barrier. The Eighth Ohio and Stannard's brigade execute maneuvers to flank the Confederate attack. When the Confederate forces come close to the Union lines, the defenders move up to engage. (This is exaggerated in the present simulation for testing purposes.) After taking heavy losses, the Union forces pull back, and the Rebels press the attack until they, in turn, take heavy casualties and retreat in disorder.
In the second (discrete agent) simulation, it is not possible to replicate the interaction of the units with the terrain in the same way. Here, the discrete units respond the terrain at their centers, but the balance between cohesiveness and spreading in response to the environment that is captured by the continuous flow model is not present. The outcome of this discrete agent simulation is less realistic in this way: this model cannot fully capture the way in which terrain slows the pace of battle and favors the defenders.
In ongoing research, we are working to improve the realism of the representation of historical events, working toward a parametric study of the effect of changes in strategy and the uncertainty in historical force strengths on the outcome of the battle.