The time-domain methods in computational electromagnetics can be categorized into two classes. One is the explicit time-domain method; the other is the implicit time-domain method. Explicit methods can avoid solving a matrix, while implicit methods generally require a matrix solution. The time step of a traditional explicit method is restricted by the smallest space step for ensuring the stability of a time-domain simulation. Existing unconditionally stable methods are all implicit methods.
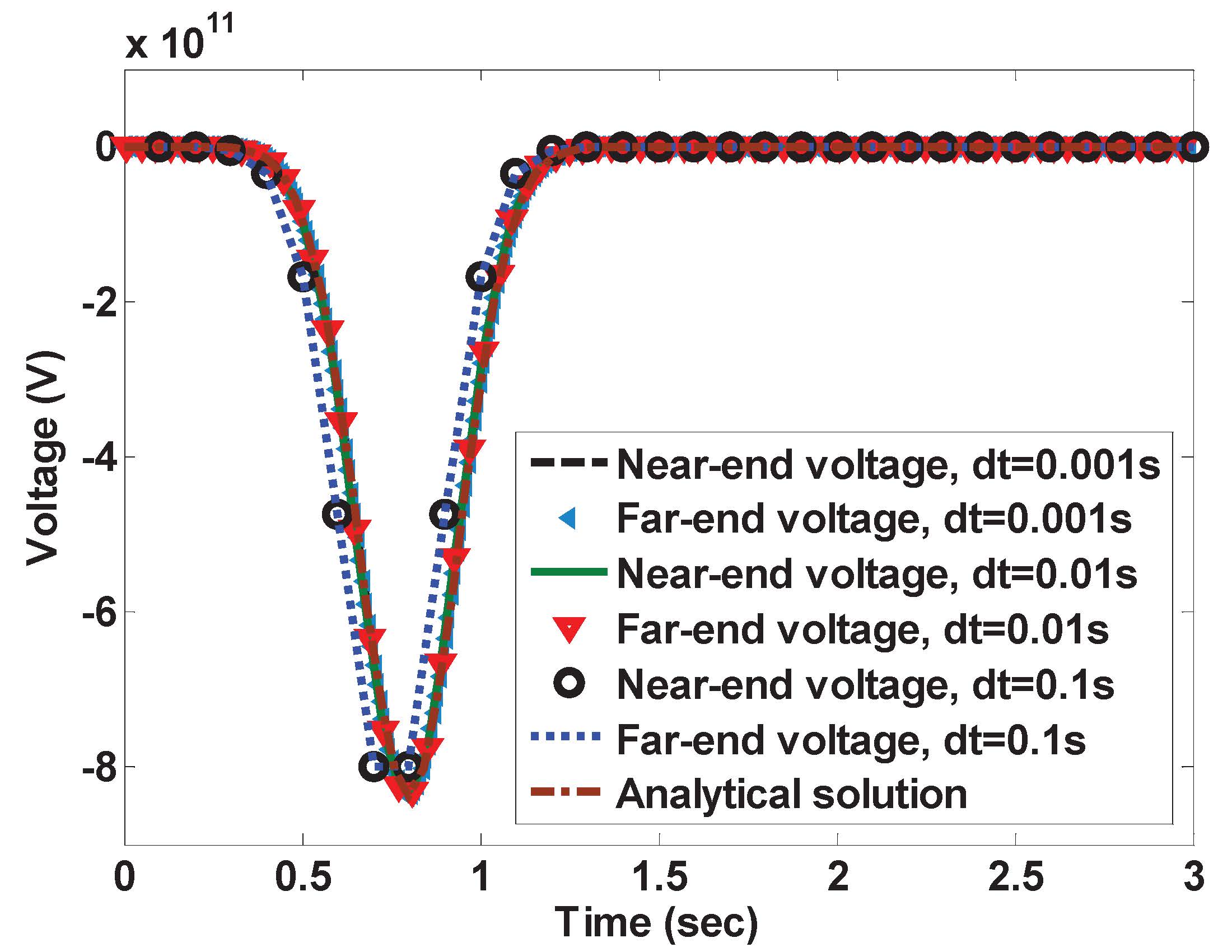
This problem has prevented the existing time-domain methods from analyzing large-scale multiscaled problems in feasible run time and memory, where fine features can be orders of magnitude smaller than the largest feature size. In this work, we create explicit time-domain methods that are unconditionally stable, which removes a major limit in time-domain analysis. The method retains the strength of an explicit time-domain method in being matrix free, while eliminating its shortcoming in time step when the smallest space step is small as compared to the working wavelength. In the example shown in the figure, a conventional explicit method requires a time step as small as 1.0363e-15 s to be stable, whereas the time step required by sampling accuracy for the input spectrum is 13 orders of magnitude larger. As shown in the figure, first, the proposed method is stable regardless of the choice of the time step; second, it is capable of using the time step solely determined by sampling accuracy to generate accurate results.
Selected Publications
- [1] Q. He, H. Gan, and D. Jiao, "Explicit Time-Domain Finite-Element Method Stabilized for an Arbitrarily Large Time Step," IEEE Trans. Antennas and Propagation, vol. 60, no. 11, pp. 5240 - 5250, 2012.
- [2] M. Gaffar and D. Jiao, "An Explicit and Unconditionally Stable FDTD Method for Electromagnetic Analysis," IEEE Trans. Microw. Theory Tech., vol. 62, no. 11, pp. 2538-2550, Nov. 2014.
-
[3] M. Gaffar and D. Jiao, "An Alternative Method for Making an Explicit FDTD Unconditionally Stable," IEEE International Microwave Symposium, 2015.
-
[4] W. Lee and D. Jiao, "A New Explicit and Unconditionally Stable Time-Domain Finite-Element Method," IEEE Int. Symposium Antennas and Propagation, 2015.