Electronic Structure of Confined Devices with 8-band k.p
The carriers in the extrema of various energy bands govern the physics of semiconductors. The neighbourhood of these band extrema and the shape of the energy surfaces yield qualitative information about the dispersion relationship. The neighbourhood properties are obtainable through a perturbative approach while the shape of the energy surfaces manifests themselves through symmetry arguments. In this is contained the crux of the k.p theory.
Purpose of the simulator
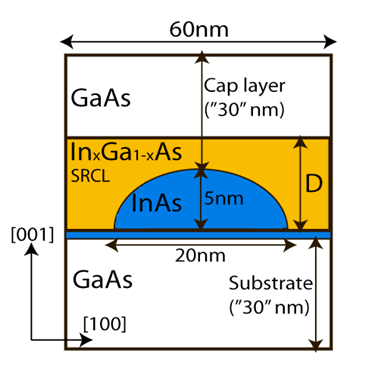
To develop a full 3D discretized 8-band k.p model to calculate the band structures of quantum wells, wires, and dots.
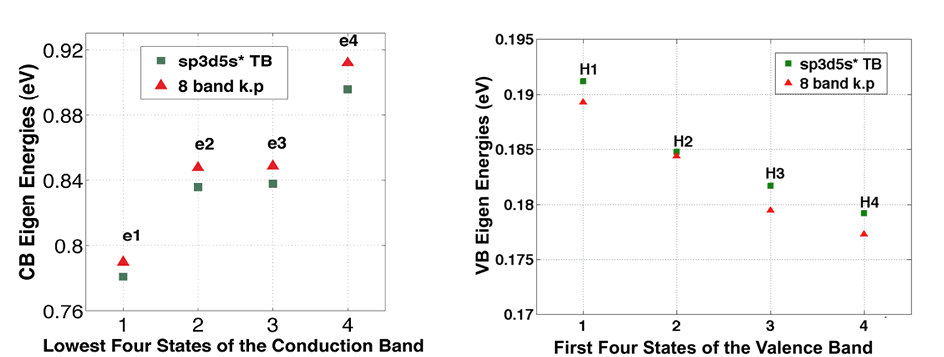
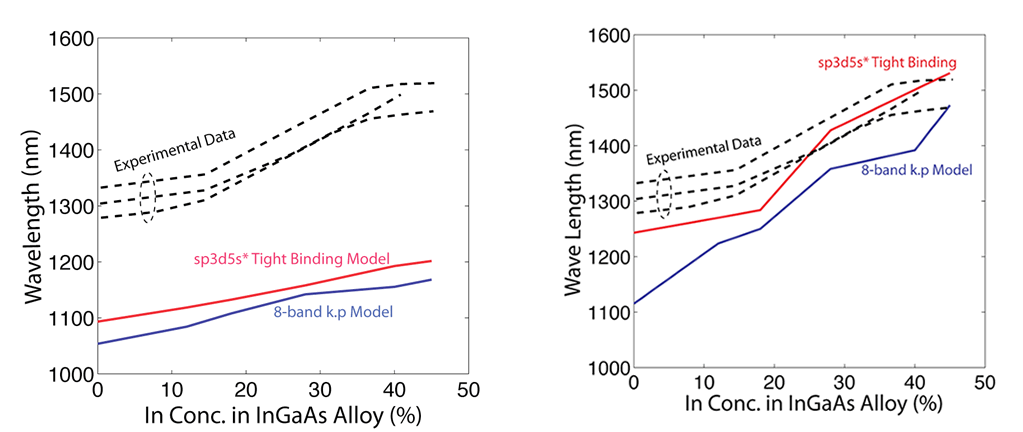
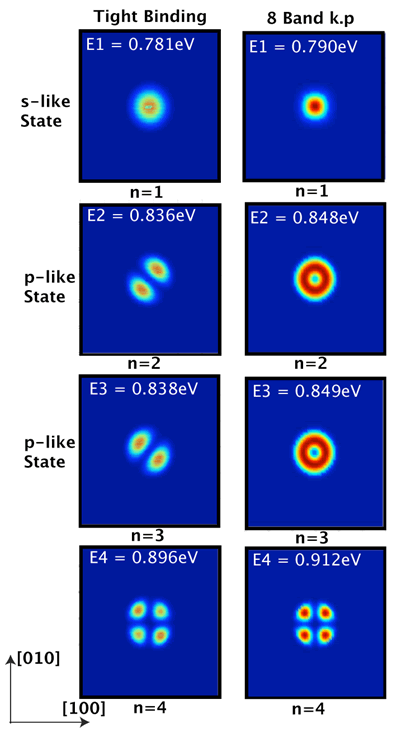
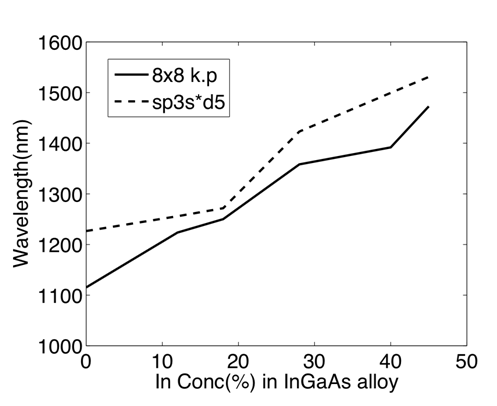
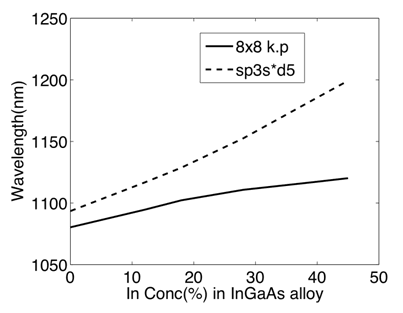
Direct Comparison of continuum and atomistic methods of electronic structure calculation
Provide electronic dispersion to model hole transport
Capabilities of the current simulator
To capture the electronic properties of bulk, wells, wires, and dots we developed a k.p solver. The simulator has the following capabilities:
- 3D discretized and MPI parallelized C++ 8-band k.p solver
- Strain effects included by the following methods
- Continuum Elastic Theory
- Interpolation of strain field obtained through the Valence Force Field (VFF)
- Scope to simulate arbitrarily directed external strain field
- Can handle Zinc Blende and Wurtzite crystals
Results achieved so far
|
|
|
|
|
|
|
|
|
|
Associated publications
Multiscale Modeling of Quantum Dot Heterostructures, Parijat Sengupta, Sebastian Steiger, Sunhee Lee, Hoon Ryu and Gerhard Klimeck. MRS Proceedings,Spring Meeting, 2011