Due 12/9

Graphs

Learning goals

You should learn how to:

Write C code to generate graphs and analyze their structure.
Apply graph theoretic techniques, data structures, and algorithms for problem solving.
Apply a queue data structure to solve a problem with a graph.

Overview

In this assignment, you will write C code that creates graphs and analyzes their structure.

The code for creating graphs could potentially be used to generate test cases for other code that analyzes graphs. (Keep this in mind if you continue studying graphs and doing sample interview questions.)

About the code

This code stores the graph as an adjacency matrix. Edges are stored in the .weights_from_to field of the Graph struct object. For example, if graph.weights_from_to[2][3] == 5, it means there is an edge from vertex 2 to vertex 3 with weight 5.

The graph is a weighted graph. It may or may not be cyclic and/or connected.

We have provided the code for creating a skeleton graph (i.e., no edges). You provide the edges.

Getting Started

Get the starter code

Change to your directory for this course.

you@ecegrid-thin1 ~/
$

cd 368

Get the starter code.

you@ecegrid-thin1 ~/368/
$

368get hw07

This will write the following files: … 1. hw07/Makefile 2. hw07/graph.c 3. hw07/graph.h 4. hw07/test_graph.c Ok? (y/n)y 4 files were written

you@ecegrid-thin1 ~/368/
$

cd hw07

you@ecegrid-thin1 ~/368/hw07
$

For your convenience, we are providing a Makefile to make it more convenient to compile, test, and submit your code. To see the commands that are available, open it up.

you@ecegrid-thin1 ~/368/hw07
$

vim Makefile

In summary:

make … compiles your code.
make test … compiles your code and runs ./test_graph.
make submit … submits the required files. (Double-check!!!)
make valgrind … compiles your code and checks for memory faults using Valgrind.

Requirement: incremental submissions

You are required to submit at least 6 times, at least 10 minutes apart with significant differences in the code—and the amount of working functionality—between these submissions. Submitting even more often is strongly encouraged as it saves backups of your work, in case something goes wrong.

Requirements

Your submission must contain all files included in the starter code. We will only check the following file:

file	contents
graph.c	functions
		`get in degree(Graph graph, int idx of vertex to)` → return type: int Return the number of edges leading to the vertex at index `idx_of_vertex_to`.
		`get out degree(Graph graph, int idx of vertex from)` → return type: int Return the number of edges leading from the vertex at index `idx_of_vertex_from`.
		`create random complete graph(size t num vertices)` → return type: Graph Create a complete graph. From every vertex, there should be an edge leading to every other vertex.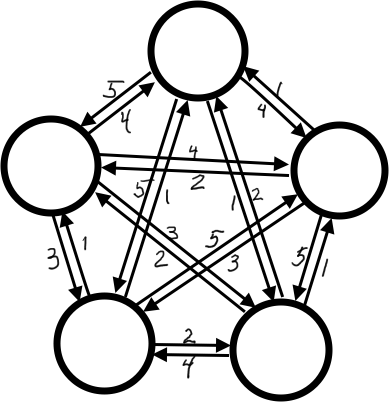 Weights should be random. Call `_get_random_weight(…)`. In-degree and out-degree of every node should be num_vertices - 1. Do not add any self-loops (i.e., edge from node to itself.)
		`create random cycle graph(size t num vertices)` → return type: Graph Create a cycle graph with `num_vertices` vertices.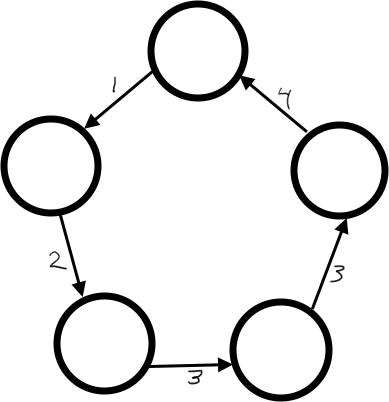 There should be exactly one Euler cycle, and no other edge. Arrangement of the vertices in the cycle should be random. Weights should be random. Call `_get_random_weight(…)`. In-degree and out-degree of every node should be 1. Do not add any self-loops (i.e., edge from node to itself.)
		`create random wheel graph(size t num vertices)` → return type: Graph Create a wheel graph with `num_vertices` vertices.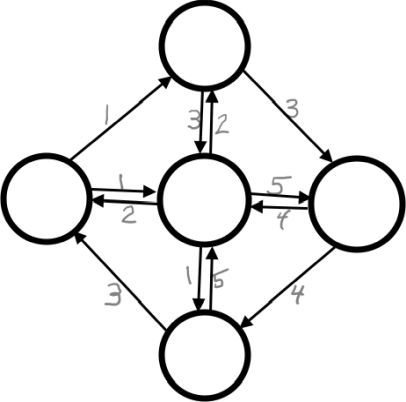 Order should be random. Weights should be random. Call `_get_random_weight(…)`. Choose one hub node. There should be a pair of edges between the hub node and every other node—in both directions. In-degree and out-degree of the hub node should be num_vertices - 1. In-degree and out-degree of every other node should be 2. Do not add any self-loops (i.e., edge from node to itself.)
		`create random graph(size t num vertices, size t num edges)` → return type: Graph Create a graph with `num_vertices` and `num_edges` edges between randomly selected pairs of vertices.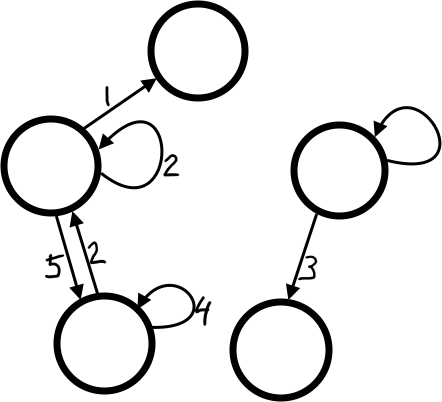 Create num_edges edges between randomly selected pairs of vertices. Weights should be random. Call `_get_random_weight(…)`. The resulting graph may or may not be (strongly or weakly) connected.
		`is strongly connected(Graph graph)` → return type: bool Return `true` if the graph is strongly connected, i.e., for every pair of vertices u, and v, if u ≠ v, there is a path from u to v. Path can be via other nodes. Strongly connected does not require an edge between every pair of nodes. (That is a complete graph.) Return `false` if it is not strongly connected.

We ask that you include the other files from the start to aid in troubleshooting.

Do not modify the function signatures of the required functions above.
Do not modify the Graph struct type.
You are responsible for testing your code. You should put any tests in test_graph.c.c.
In case of any corrections announced by email, apply them and ensure that your code works.
Running time should be reasonable for each operation. Follow the spirit of the assignment.

Only the following external header files, functions, and symbols are allowed in graph.c.

header	functions/symbols	allowed in…
stdbool.h	`bool`, `true`, `false`	`*`
stdio.h	`*`	`*`
stdint.h	`*`	`*`
assert.h	`assert`	`*`
stdlib.h	`*`	`*`

All others are prohibited unless approved by the instructor. Feel free to ask if there is something you would like to use.

Use create_graph_with_no_edges(…) to create a graph structure to start with. Caller is responsible for freeing.
Follow the policies on homework (including the base requirements) and academic integrity. For example:
- Do not copy code from generated by Chat-GPT (or other GenAI tools).
- Do not copy code found on the web.

Submit

To submit HW07 from within your hw07 directory, type

make submit

That should result in the following command: 368submit HW07 graph.c test_graph.c graph.h credit.txt Makefile

Q&A

…
…

Updates

There are no updates to HW07 so far.

Data Structures

Fall 2023 ECE 36800 :: Purdue University