Data Structures

Fall 2023 ECE 36800 :: Purdue University

Due 10/3

Selection

Learning goals

You should learn how to:

  1. Implement a divide-and-conquer selection algorithm.
  2. Implement the foundations of the quicksort algorithm. (This assignment is not quicksort, but it is very similar.)
  3. Reason about the average case and worst case running time of an algorithm.

Overview

In class, we discussed the quicksort algorithm for sorting arrays in memory. With this assignment, you will use a very similar strategy to solve a closely related problem: selection.

The selection problem is to find the kth smallest element in an array. A naïve solution would be to simply sort the array and then return array[k]. But if you only need the kth smallest element, sorting the entire array is a waste of computation.

Getting Started

Get the starter code

Change to your directory for this course.

you@ecegrid-thin1 ~/ $ cd 368

Get the starter code.

you@ecegrid-thin1 ~/368/ $ 368get hw03
This will write the following files: 1. hw03/Makefile 2. hw03/answers.txt 3. hw03/credit.txt 4. hw03/select.c 5. hw03/select.h 6. hw03/special_test_cases.h 7. hw03/test_select.c 8. hw03/test_utils.c 9. hw03/test_utils.h Ok? (y/n)y 9 files were written
you@ecegrid-thin1 ~/368/ $ cd hw03
you@ecegrid-thin1 ~/368/hw03 $

For your convenience, we are providing a Makefile to make it more convenient to compile, test, and submit your code. To see the commands that are available, open it up.

you@ecegrid-thin1 ~/368/hw03 $ vim Makefile

In summary:

  • make … compiles your code.
  • make test … compiles your code and runs ./test_select.
  • make submit … submits the required files. (Double-check!!!)
  • make valgrind … compiles your code (if needed) and checks for memory faults using Valgrind.

Requirement: incremental submissions

You are required to submit at least 6 times, at least 10 minutes apart with significant differences in the code—and the amount of working functionality—between these submissions. Submitting even more often is strongly encouraged as it saves backups of your work, in case something goes wrong.

Compile

To compile:

you@ecegrid-thin1 ~ $ cd 368
you@ecegrid-thin1 ~/368 $ cd hw03
you@ecegrid-thin1 ~/368/hw03 $ gcc select.c test_select.c test_utils.c -o test_select

Writing the code

Follow the test-driven development process. We have made this easy for you by giving you a set of starter test cases (test_select.c), as well as some utilities to help with testing (test_utils.c and test_utils.h).

  1. TODO
  2. Submit.

Outline of a solution

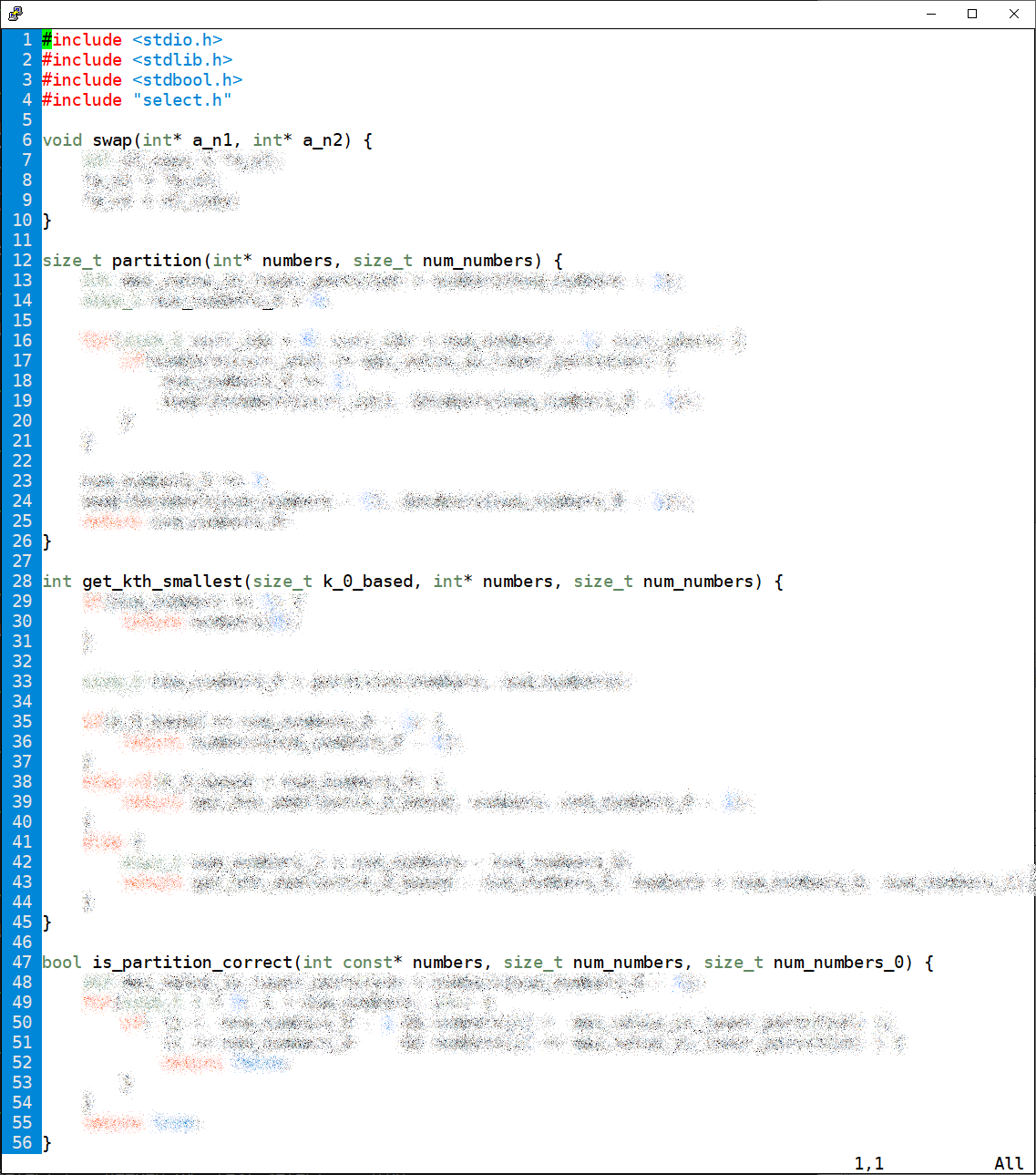
To help you understand the algorithm we are using for this homework, we are providing a redacted screenshot of the instructor's solution, with copious annotations.

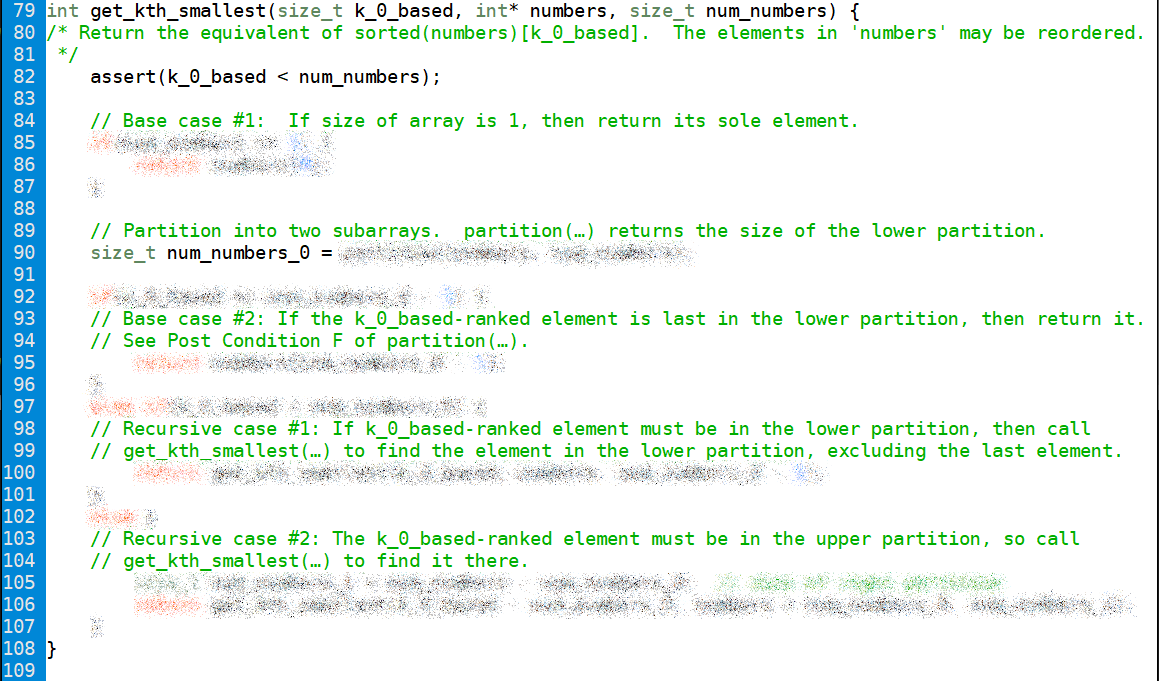
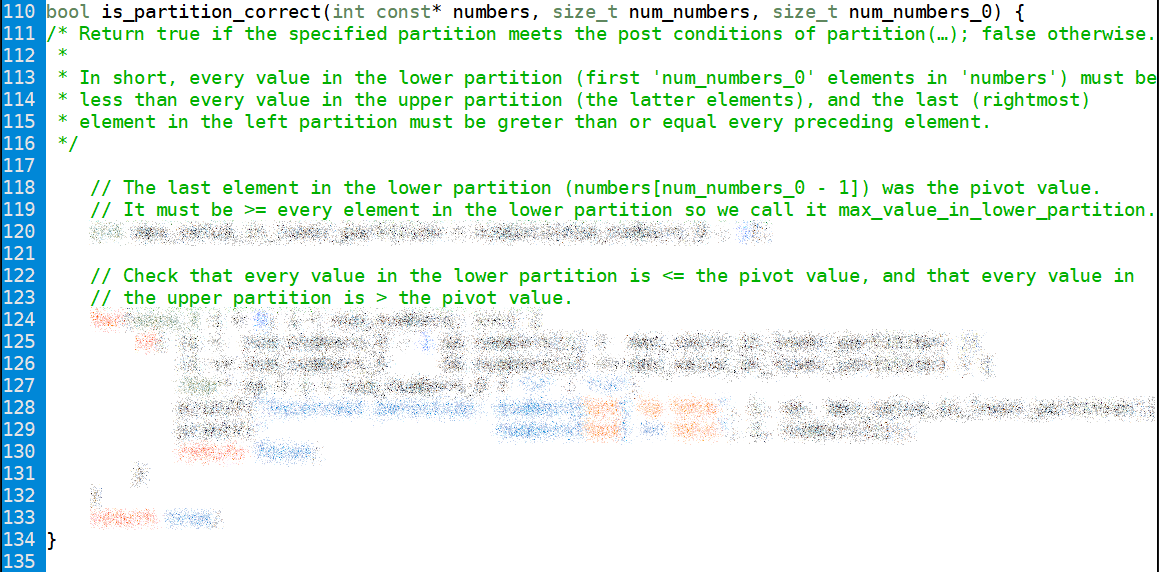
screenshot of select.c in instructor's solution screenshot of select.c in instructor's solution screenshot of select.c in instructor's solution screenshot of select.c in instructor's solution screenshot of select.c in instructor's solution screenshot of select.c in instructor's solution

How much work is this?

Relative to the provided skeleton, the instructor's select.c adds/modifies 36 source lines of code (SLOC), not counting assertions.

“Source lines of code (SLOC)” always excludes comment lines and blank lines. Instructor's solution follows all code quality standards and uses no advanced methods or C language features.

The screenshot below shows the instructor's solution with comments, assertions, and optional calls to printf(…) removed.

screenshot of select.c in instructor's solution

Requirements

  1. Your submission must contain each of the following files, as specified:
    file contents
    select.c functions
    swap(int✶ a n1, int✶ a n2)
    → return type: void
    Swap the value at address a_n1 with the value at address a_n2.
    • Post condition: Upon return, the value at address a_n1 should be the value previously at a_n2, and vice versa.
    is partition correct(int const✶ numbers, size t num numbers, size t num numbers 0)
    → return type: bool
    Check if the values in array numbers have already been correctly partitioned. This will be used to test your partition(…) function.
    • numbers is an array of int.
    • num_numbers is the number of elements in the entire array (including both partitions).
    • num_numbers_0 is the number of numbers in the left (first) subarray.
    • The “pivot value” used in the partition(…) is numbers[num_numbers_0 - 1].
    • Every value in the first num_numbers_0 elements of numbers should be less than all values in the subsequent elements.
    • Return true if the values in numbers are already correctly partitioned such that all values in numbers[0] through numbers[num_numbers_0 - 1] are less than all values in numbers[num_numbers_0] through numbers[num_numbers - 1].
    partition(int✶ numbers, size t num numbers)
    → return type: size t
    • Partition the array numbers into two subarrays by swapping values until, for some index num_numbers_0, all values in numbers[0] through numbers[num_numbers_0 - 1] are less than all values in numbers[num_numbers_0] through numbers[num_numbers - 1].
    • Use whatever strategy you like for picking the pivot and performing the partition, as long as you meet the post-conditions below.
    • partition(…) must run in O(num_numbers) run time.
    • Post conditions - Upon return of partition(…), the following conditions must be true:
      1. The first 'num_numbers_0' elements in 'numbers' are all less than the latter elements. In other words, every element in numbers[0]…numbers[num_numbers_0 - 1] is less than every element in numbers[num_numbers_0]…numbers[num_numbers - 1].
      2. Number of elements in the lower partition (num_numbers_0) is >= 1.
      3. The lower partition consists of numbers[0]…numbers[num_numbers_0 - 1]. It contains the smallest num_numbers_0 values.
      4. The upper partition consists of numbers[num_numbers_0]…numbers[num_numbers - 1]. It contains the largest (num_numbers - num_numbers_0) values.
      5. Every value in the lower partition is less than every value in the upper partition.
      6. The highest-index (rightmost) element in the lower partition (i.e., the pivot value) contains the max of the values in the lower partition. In other words, numbers[num_numbers_0 - 1] is >= every value in numbers[0]…numbers[num_numbers_0 - 1].
      (Note: Some of these post conditions are saying the same thing, but in different ways.
    get kth smallest(size t k 0 based, int✶ numbers, size t num numbers)
    → return type: int
    Return the kth smallest value in numbers.
    • get_kth_smallest(…) must run in O(num_numbers) time, in the expected average case.
      • It will run in O(num_numbers²) in the worst case.
    special_test_cases.h test data
    TEST NUMBERS O N
    Array of numbers that, if passed to get_kth_smallest(…) would result in O(num_numbers) running time to find the kth smallest element, for any value k_0_based in [0, num_numbers].
    • TEST_NUMBERS_O_N must contain at least 16 values.
    • Explain in answers.txt how you know it will take O(n) running time.
    TEST NUMBERS O N2
    Array of numbers that, if passed to get_kth_smallest(…) would result in O(num_numbers²) running time to find the kth smallest element, for any value k_0_based in [0, num_numbers].
    • Other requirements are the same as for TEST_NUMBERS_O_N.
    answers.txt text
    Rationale for TEST_NUMBERS_O_N
    Rationale for TEST_NUMBERS_O_N2
    credit.txt text
    Q1: Online resources
    Q2: GenAI resources
  2. Do not modify select.h, test_utils.c, or test_utils.h.
    • You should modify test_select.c to ensure adequate testing.
  3. Use of assert(condition) is strongly encouraged, but the condition must not have any side effects.
  4. Submit at least 6 times, with at least 10 minutes between each submission.
  5. Your code must meet all code quality standards.
    1. ⚠ Do not use typecasts anywhere in HW03.
  6. Only the following external header files, functions, and symbols are allowed in select.c.
    header functions/symbols allowed in…
    stdbool.h bool, true, false *
    stdio.h * test_select.c
    stdio.h printf is_partition_correct(…) (in select.c)
    assert.h assert *
    stdlib.h EXIT_SUCCESS test_select.c
    All others are prohibited unless approved by the instructor. Feel free to ask if there is something you would like to use.
    1. ⚠ malloc(…) is not allowed anywhere in select.c.
  7. Follow the policies (including the base requirements) and academic integrity. For example:
    • Do not copy code from generated by Chat-GPT (or other GenAI tools).
    • Do not copy code found on the web.

Submit

To submit HW03 from within your hw03 directory, type 368submit HW03 select.c test_select.c test_utils.c test_utils.h

Q&A

  1. I want to use a global variable to track how many times a line is executed with various inputs. How can I declare the variable in one file (i.e., test_select.c) but access/modify it in another file (i.e., select.c)?

    Here is an example:

    a.c 
    #include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <assert.h>

void foo();  // declaration (would normally be in a .h file)

int g_num_calls_to_foo = 0;

int main(int argc, char* argv[]) {
    printf("g_num_calls_to_foo == %d\n", g_num_calls_to_foo);
    foo();
    foo();
    foo();
    printf("g_num_calls_to_foo == %d\n", g_num_calls_to_foo);
    return EXIT_SUCCESS;
}
    b.c
    extern int g_num_calls_to_foo;

void foo() {
    g_num_calls_to_foo += 1;
}

Updates

There are no updates to HW03 so far.