Neural Network TLU Algorithm Demonstration
by Andy Byerly & Jason Ridenour 

Variable Information
  INPUT is an [n X p] matrix.
    the p columns of input are the n-dimensional training vectors
  CLASS is a [1 X p] row vector.
    the p elements of class are the (integer) classes of each training vectors

Examples
  Problem from Funwork Set #1
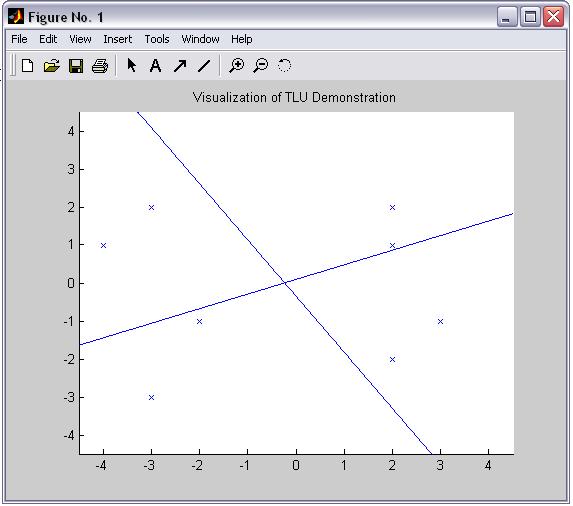
  INPUT = [2,2,2,3,-3,-4,-2,-3;1,2,-2,-1,2,1,-1,-3]
  CLASS = [1,1,2,2,3,3,4,4]

  Problem from Hagan, Demuth, and Beale
  INPUT = [1,1,2,2,-1,-2,-1,-2;1,2,-1,0,2,1,-1,-2]
  CLASS = [1,1,2,2,3,3,4,4]
AN INTERACTIVE JAVASCRIPT TLU SIMULATION:
The Threshold Logic Unit (TLU) Algorithm develops a weight matrix and a threshold matrix that 
describes lines which seperate the various class inputs.  Below, you will see a Javascript simulation
of the TLU algorithm as well as the code to a Matlab TLU simulation and a Matlab example.
INPUT = [x11,x12,...,x1p;x21,x22,...,x2p;...;xn1,xn2,...,xnp]
INPUT =

CLASS = [c1,c2,...,cp];
CLASS =

RUN TLU(INPUT,CLASS)


* Javascript program idea originates from project of Ricky Chan and Aaron Cramer
A MATLAB TLU SIMULATION PROGRAM FILE:
%   TLU	Algorithm
%	Determines weight and threshold vector for given input and classes
%	INPUT
%		INPUT:		member of a class
%       CLASS:      class of respective input
%                   class defined as binary input of ones and neg ones
%	Outputs
%		WEIGHT: 	vector of weights on input syapses
%		THRESHOLD:	firing threshold of perceptron

function [WEIGHT,THRESHOLD] = TLU(INPUT, CLASS)
if nargin ~= 2
	fprintf('Error in TLU: Incorrect number of inputs\n');
	return
end

WEIGHT = rand(size(INPUT,1),size(CLASS,1)); % Random initial WEIGHT vector
THRESHOLD = rand(size(CLASS,1),1);          % Random initial THRESHOLD vector
FLAG = 1;                                   % FLAG only cleared when all outputs agree

while FLAG ~= 0
    FLAG = 0;
    for i = 1:size(CLASS,2)
        if CLASS(:,i) ~= sign(WEIGHT' * INPUT(:,i) - THRESHOLD)
            FLAG = 1;
        end
        WEIGHT = WEIGHT + .5 * INPUT(:,i)*(CLASS(:,i) - sign(WEIGHT' * INPUT(:,i) - THRESHOLD))';
        THRESHOLD = THRESHOLD - .5 * (CLASS(:,i) - sign(WEIGHT' * INPUT(:,i) - THRESHOLD));
    end
end

% Plot results and return
% This plot only works for [2 X n] dimensional INPUTS
maximum = max(max(abs(INPUT))) + 0.5;
x = -maximum:.01:maximum;
close;
figure(1);
hold on;
for i = 1:size(CLASS,2)
  plot(INPUT(1,i),INPUT(2,i),'x')
end
for i = 1:size(WEIGHT,2)
  y(i,:) = -WEIGHT(1,i)*(x+THRESHOLD(i,1))/WEIGHT(2,i);
  plot(x,y(i,:))
end
axis([-maximum maximum -maximum maximum]);
title('Visualization of TLU Demonstration')
return
EXAMPLE OF MATLAB PROGRAM RESULTS:
>> INPUT =

     2     2     2     3    -3    -4    -2    -3
     1     2    -2    -1     2     1    -1    -3

>> CLASS =

    -1    -1    -1    -1     1     1     1     1
    -1    -1     1     1    -1    -1     1     1

>> [WEIGHT,THRESHOLD] = TLU(INPUT, CLASS)

WEIGHT =

   -1.8790    0.7159
   -0.5492   -2.1072


THRESHOLD =

    0.2731
    0.2548