



|
Maryam, Roberta, and Mike’s Funwork #3 |
|
WTA and Hopfield Networks |
|
Hopfield Net |
|
In order to learn about Hopfield Networks, a simple two-neuron network was examined. In this case, the equations had the form: |
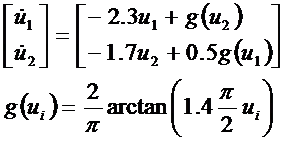
|
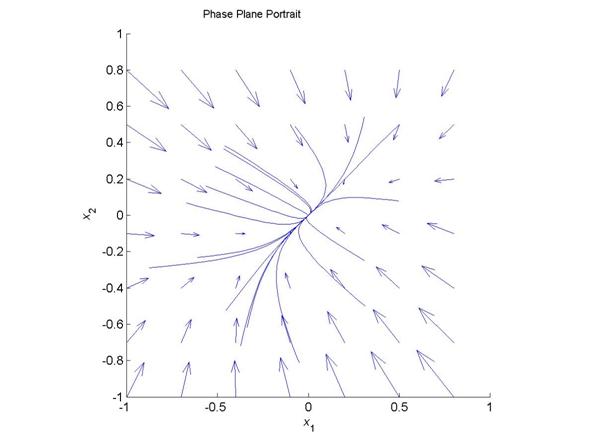
In order to determine the direction of the solutions, the directional derivatives were examined, and the phase plane portrait shown in Figure 1 was the result. |
|
By examining the trajectories (and more importantly the termination of these trajectories) the stable points for the system can be found. After determining the trajectories and stopping points for several different initial conditions, only one stable point was found. The stable point was very close to (1e-10, 1e-10), which is practically zero considering the error due to the numerical approximation of the differential function. In order to verify the numerical answer by inspection, the phase plane portrait above was examined, and it seems clear that the stable point is in the center of the graph. The Matlab m-file for this segment is shown on the following page, “Hopfield Code”. |
|
Figure 1. Phase plane portrait of the system described in the equations above. Note the convergence to a single center point. |