Steven E. Lamberson, Jr.
October 9, 2004
In all the previous homework assignments we have discussed supervised neural networks - that is, networks that require a "teacher" to "instruct" them before they can properly perform their task. Now we will be discussing the Winner-take-all (WTA) neural net, which is one of the types of neural networks classified as an unsupervised (or self-organized) network. The WTA is capable of learning as it is going, and does not need a particular learning phase because it learns as it goes.
In order for this to work, we must assume that we know the number of classes, p, and must set up a network with p neurons. The weight vectors for each neuron must be initialized and normalized. Then we must normalize and present the patterns that are to be classified by the neural net. Each pattern is presented one at a time, and then compared to the weight vectors of the network by means of the dot product. The weight vector that produces the smallest dot product with the pattern is the closest to the pattern and will be declared the winner. This winner will be updated by adding the current weight to the difference between the pattern and the weight, multiplied by some search step size. This update algorithm is expressed mathematically below.
![]()
The losing weight vectors (or the not-winning weight vectors if you are concerned for the feelings of the neurons) will remain the same. After some stopping criteria is met, the network will have weight vectors that classify the groups of patterns as best as possible given the number of classes.
back to beginning of WTA section
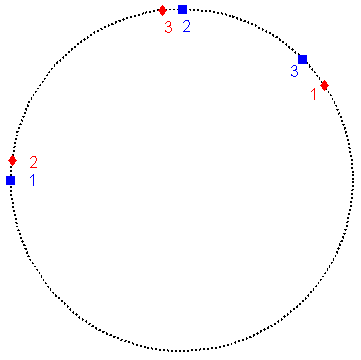
Let us look at the training patterns and initial weight vectors described below. They are shown graphically on the unit circle (training patterns are blue, weights are red).
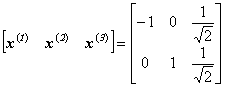
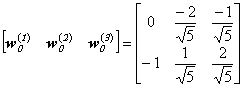
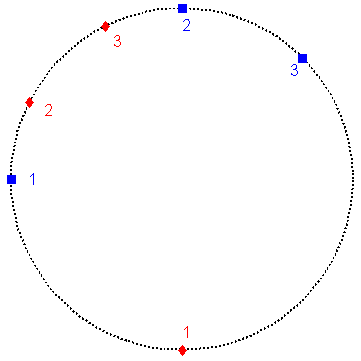
After the network has been exposed to the training patterns, the weights should move closer to the closest training pattern. Ideally, with this problem, one would end up with all the weights predicting all the patterns exactly, since there are 3 patterns and 3 neurons. Below are the resulting weights and their graphical representation after presenting the patterns to the network twice, in the order 1, 2, 3, 1, 2, 3. (The search step size was 0.5).
![]()
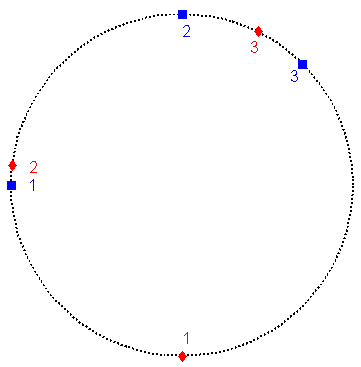
Note how the first weight vector has not moved. This is called a "dead neuron" by some, and is a result of the fact that no matter what order the patterns are presented, one of the other weights will always be closer to the presented pattern than neuron one. Neuron 3 travels between patterns 2 and 3, and neuron 2 heads directly toward pattern 1. If this pattern were presented many more times, neuron 1 would still be where it is since it is never updated, neuron 3 will be approximately where it is (always between patterns 2 and 3), and neuron 2 will become equal to pattern 1. The only way to fix this is to move the initial value of neuron 1 to where it is close to one of the training patterns. This has been done so below.
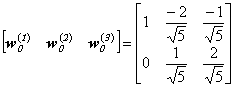
![]()
Note that now neuron 1 predicts pattern 3, neuron 2 predicts pattern 1, and neuron 3 predicts pattern 3. The predictions are not precise, as the patterns were only presented twice (in the order 1, 2, 3, 1, 2, 3). If we were to present the patterns more, the predictions would become more precise. The following picture shows the results of presenting the patterns 20 times each..
![]()

back to beginning of WTA section
I used the following MATLAB m-files to perform this assignment:
hom3a.m -- does the particulars of this problem
WTA.m -- contains the algorithm that actually updates the WTA network
back to beginning of WTA section
The Hopfield neural network is a dynamical system that can be realized with the following circuit layout.
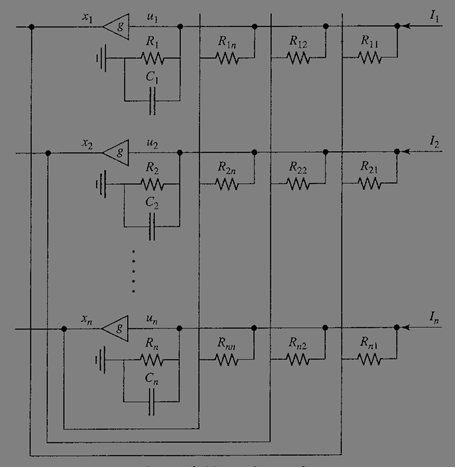
Picture taken from Systems and Control by Stanislaw H. Żak
The non-linear amplifier imposes some activation function g on the input u resulting in the output x. A common choice for the activation function is the sigmoid, however there are other options. In fact, each neuron on the same network can have a different activation function. There are n amplifiers (corresponding to n neurons and n dimensions in the x vector), each having a resistance Rn and a capacitance Cn. There is also an interconnection between each neuron with resistances Rnn and external inputs In.
Skipping all the details, the dynamics of the system (for i = 1-n) can be modeled as
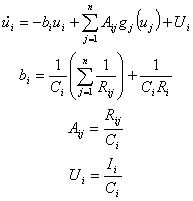
The stability of the equilibrium points of this system can be guaranteed if a few conditions are met. First, we must find all the equilibrium points of the system, and then we will have to analyze each equilibrium point separately. To analyze an equilibrium point, it is first convenient to perform a transformation so the equilibrium point is at the origin. We do so by imposing
![]()
where z is the new variable and ue is the equilibrium point in question. The first condition is that there are positive constants ri and ri such that for |xi|<ri and |xj|<rj, the neural nets interconnections satisfy the conditions:
![]()
for i = j and
![]()
where
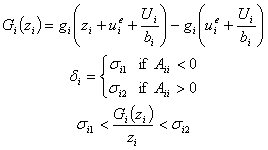
The
second condition is that there must exist some vector
![]() such that the matrix
such that the matrix
![]() is
negative definite, where the elements of
S are defined as
is
negative definite, where the elements of
S are defined as
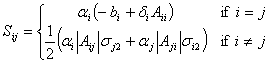
If both of these conditions are met, then the equilibrium point is uniformly exponentially stable.
back to beginning of HNN section
I constructed a Hopfield neural network using the following circuit parameters:
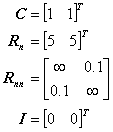
This corresponds to the dynamical system using the following parameters:
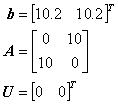
In this problem, I used the activation function described below:
![]()
A phase portrait of this system can be seen below.

There are three equilibrium points - two stable and one unstable. An analysis of the first equilibrium point yielded these parameters:
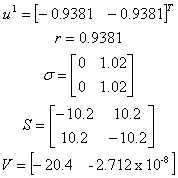
where V are the eigenvalues of S. Since all the eigenvalues of S are negative, S is negative definite. Furthermore, r is strictly possitive. Therefore, equilibrium point 1 is uniformly exponentially stable.
An analysis of the second equilibrium point yielded these parameters:

Not all of the eigenvalues of S are negative (and also r is not strictly positive), so equilibrium point 2 is not uniformly exponentially stable. In fact, near this equilibrium point the system behaves like a linear system with real eigenvalues of opposite sign, implying that the node is an unstable saddle point.
An analysis of the third equilibrium point yielded these parameters:

Since all the eigenvalues of S are negative, S is negative definite. Furthermore, r is strictly possitive. Therefore, equilibrium point 3 is uniformly exponentially stable.
back to beginning of HNN section
I used the following MATLAB m-files to perform this assignment:
hom3b.m -- does the particulars of this problem
hopnet.m -- differential equation file for use with ode23s
hopanalyze.m -- analyzes the hopfield network based on its parameters
asig.m -- contains the activation function for the non-linear amplifiers
I also used an program called pplane that runs in MATLAB and generates phase portraits (among other things).