ECE 595C
Funwork 3: Self-Organizing and
Hopfield Networks
Alex Albrecht
1. Investigation of
Self-Organizing Network
Introduction: The networks analyzed previously in this module all used teachers in order to learn presented patterns. Self-Organizing, or unsupervised networks can teach themselves using a method of computation called similarity matching. Essentially, the neuron that is most parallel (as determined by an inner product calculation) to the input vector x is the winning neuron and only its weight is updated. This type of self learning mechanism is known as Winner-Take-All or the Kohonen learning rule.
The method first proposed by Kohonen uses the descent gradient method to minimize the distance between the winning neuron and the presented pattern. The WTA algorithm can be summarized with the following steps:
STEP 1: Initailize weights and normalize.
STEP 2: Present training patterns. This is done one pattern at a times and in a random order.
STEP 3: Select winning neuron on grounds of inner product.
STEP 4: Update weight of winning neuron:
w(i)(k+1) = w(i)(k) + α(x(j) w(i)(k))
where α is the updating weight.
STEP 5: Repeat until the final criterion is met.
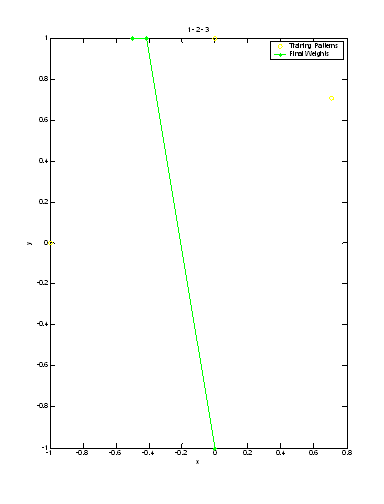
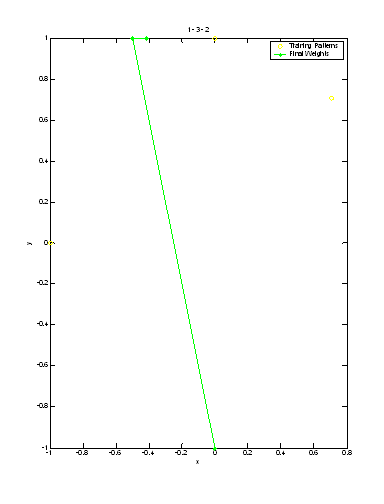
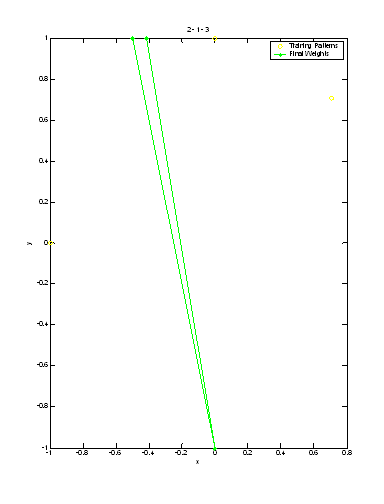
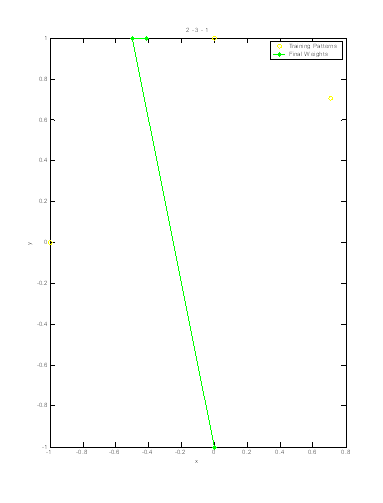
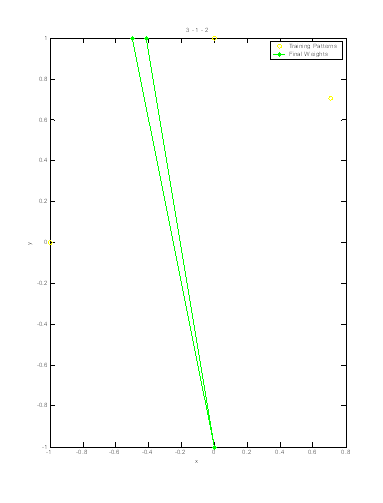
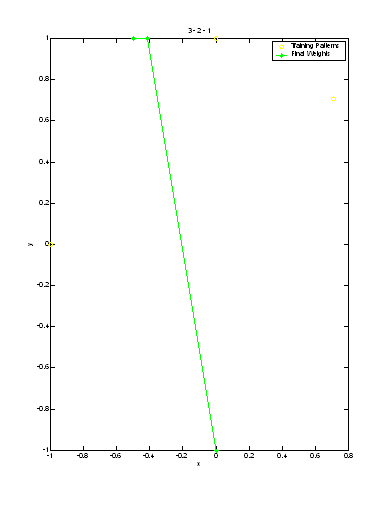
The following plots represent the final weights using the six different possible input series:
1 2 3 1 3 2
2 1 3 2 3 1
3 1 2 3 2 1
In each of the plots, it can be seen that one of the neurons does not respond. Due to its starting value, it is never the most parallel and thus its weight goes unchanged through the entire cycle. No input sequence eliminates this dead neuron. One can also see by examining the final weight vectors that they take on similar shapes in all the plots, but the order that they reach these values is varied by the input sequence.
2. Investigation of a
Hopfield Network
A Hopfield neural network is an associative memory. The network is built to have asymptotically stable states that attract neighboring states to develop in time. The process is like the evolution of a corrupted pattern towards a stored pattern. The Hopfield network can be built using a system of resistors, capacitors, and non-linear amplifiers.
MATLAB includes a function, newhop, that creates a Hopfield network of variable size. By using the input vectors as the initial layer delay conditions, we can verify that the network is stable.
Once stability has been ascertained, the network can be used to correct corrupted input vectors. Random input vectors were input to the network over 50 cycles to obtain the following network activity plot:
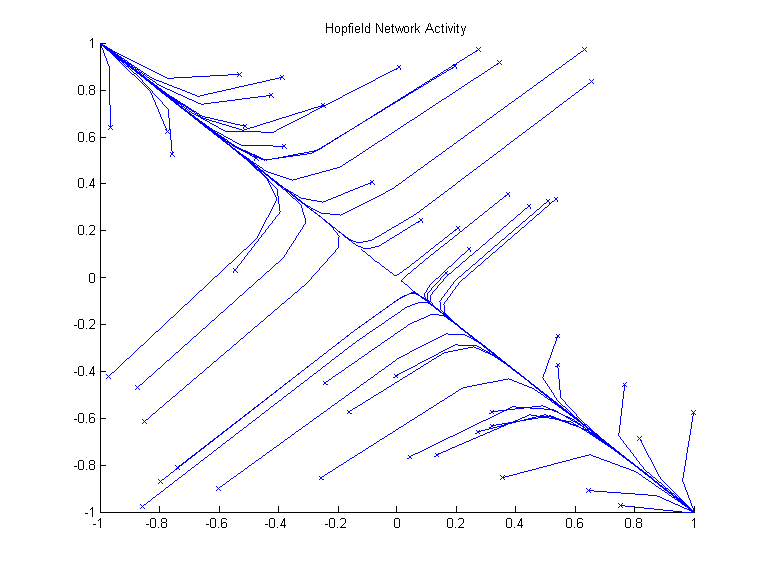
This output shows the randomized input vectors being corrected to the equilibrium points chosen for the network.
The network also has the following phase portrait:
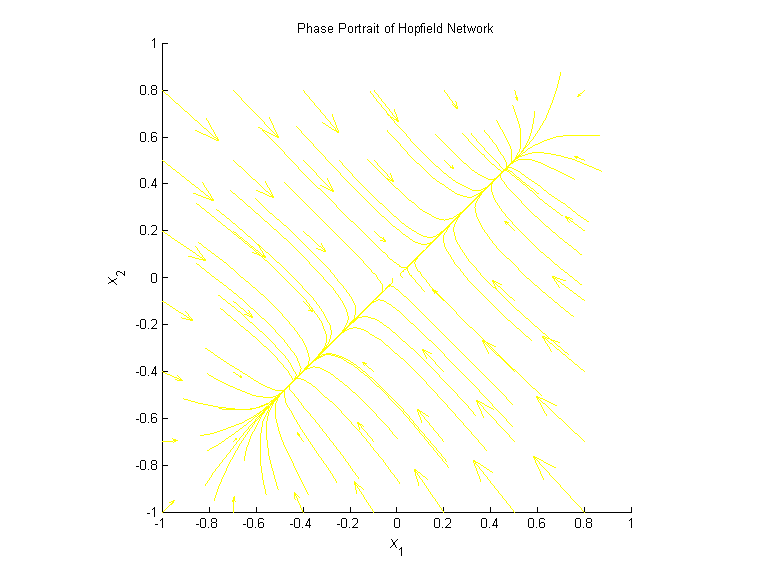
All input vectors converge to two points; {1/√(2) , 1/√(2)} and {-1/√(2) , -1/√(2)}.
3. Code and Credits
The code to produce the Network Activity graph is original and is included below:
clc
clear all
close all
x1 =
[-1;0];
x2 = [0
;1];
x3 =
[1/sqrt(2); 1/sqrt(2)];
x1 =
x1/norm(x1);
x2 =
x2/norm(x2);
x3 =
x3/norm(x3);
x = [x3 x1 x2];
w1 = [0;-1];
w2 = [-2/sqrt(5);
1/sqrt(5)];
w3 = [-1/sqrt(5);
2/sqrt(5)];
w1 = w1/norm(w1);
w2 = w2/norm(w2);
w3 = w3/norm(w3);
w = [w3 w1 w2];
order =
[x3 x1 x2];
alpha =
0.5;
for i = 1:100
innerproduct1 = dot(w1,x1);
innerproduct2 = dot(w2,x2);
innerproduct3 = dot(w3,x3);
if
innerproduct1 > innerproduct2 & innerproduct1 > innerproduct3
innerproduct =
innerproduct1;
w1 = w1 + alpha*(x2 - w1)+alpha*(x3 - w1);
w1 = w1/norm(w1);
w2 = w2;
w3 = w3;
elseif innerproduct2 > innerproduct1 &
innerproduct2 > innerproduct3
innerproduct =
innerproduct2;
w2 = w2 + alpha*(x1 - w2)+alpha*(x3 - w2);
w2 = w2/norm(w2);
w1 = w1;
w3 = w3;
else
innerproduct =
innerproduct3;
w3 = w3 + alpha*(x1 - w3)+alpha*(x2 - w3);
w3 = w3/norm(w3);
w2 = w2;
w1 = w1;
end;
wf = [w3 w1 w2];
end;
fprintf('\n');fprintf('\n');
disp('final weight matrix
is');
fprintf('\n');
wf(:,1) =
wf(:,1)/max(abs(wf(:,1)));
wf(:,2) =
wf(:,2)/max(abs(wf(:,2)));
wf(:,3) =
wf(:,3)/max(abs(wf(:,3)));
wf
colordef black
figure
plot(order(1,:),order(2,:),'oy',wf(1,:),wf(2,:),'*g-')
legend('Training
Patterns','Final Weights');
xlabel('x');
ylabel('y');
title('3 -
1 - 2');
orient tall;
The phase portrait graph was obtained using code based on code published by Stanislaw H. Żak on the website for his text, Systems and Control.
All information on this page is based on excerpts from Chapter 9 of Signals and Systems by Stanislaw H. Żak.
All graphs were created using
MATLAB.