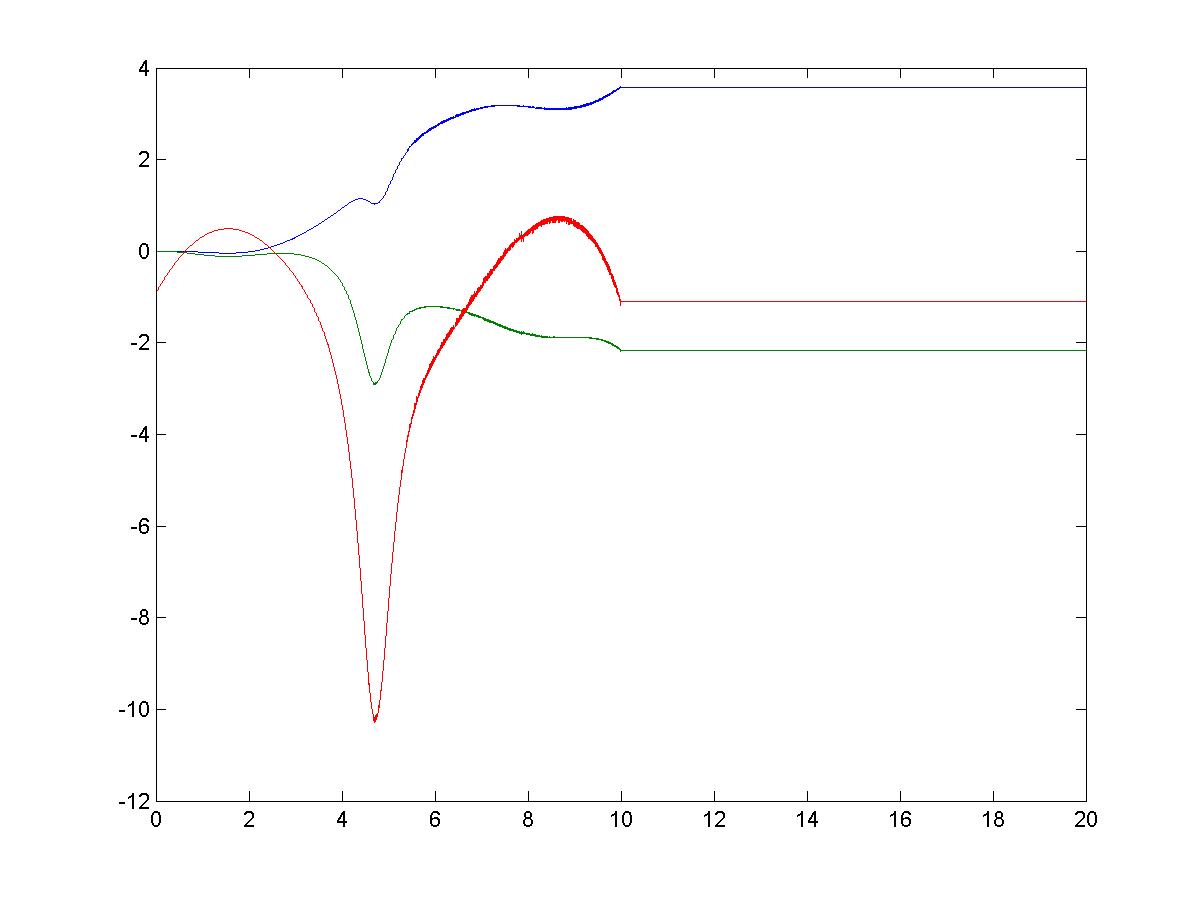
OFFLINE ADALINE LEARNING
&
TWO LAYER PERCEPTRON
[ by Aaron Cramer & Andy Byerly ]

OFFLINE ADALINE LEARNING

The offline Adaline Learning algorithm utilizes an adaptive algorithm to minimize error between the output of the plant and the desired output. The weight vectors are determined by the adaptive algorithm and are held constant at t = 10 secs. The plots are shown below. One will observe that the constant weight vectors do not maintain zero error. As the diagrams below suggest, the following simulation was completed in Simulink. The Simulink file is available here: adaline.mdl

SUBSYSTEMS
PLANT	ADALINE
PREFILTER	CONTINUOUS SIGN FUNCTION
ADAPTVE ALGORITHM

Yd AND Y vs.TIME (click on image to view larger version)

WEIGHTS vs. TIME (click on image to view larger version)

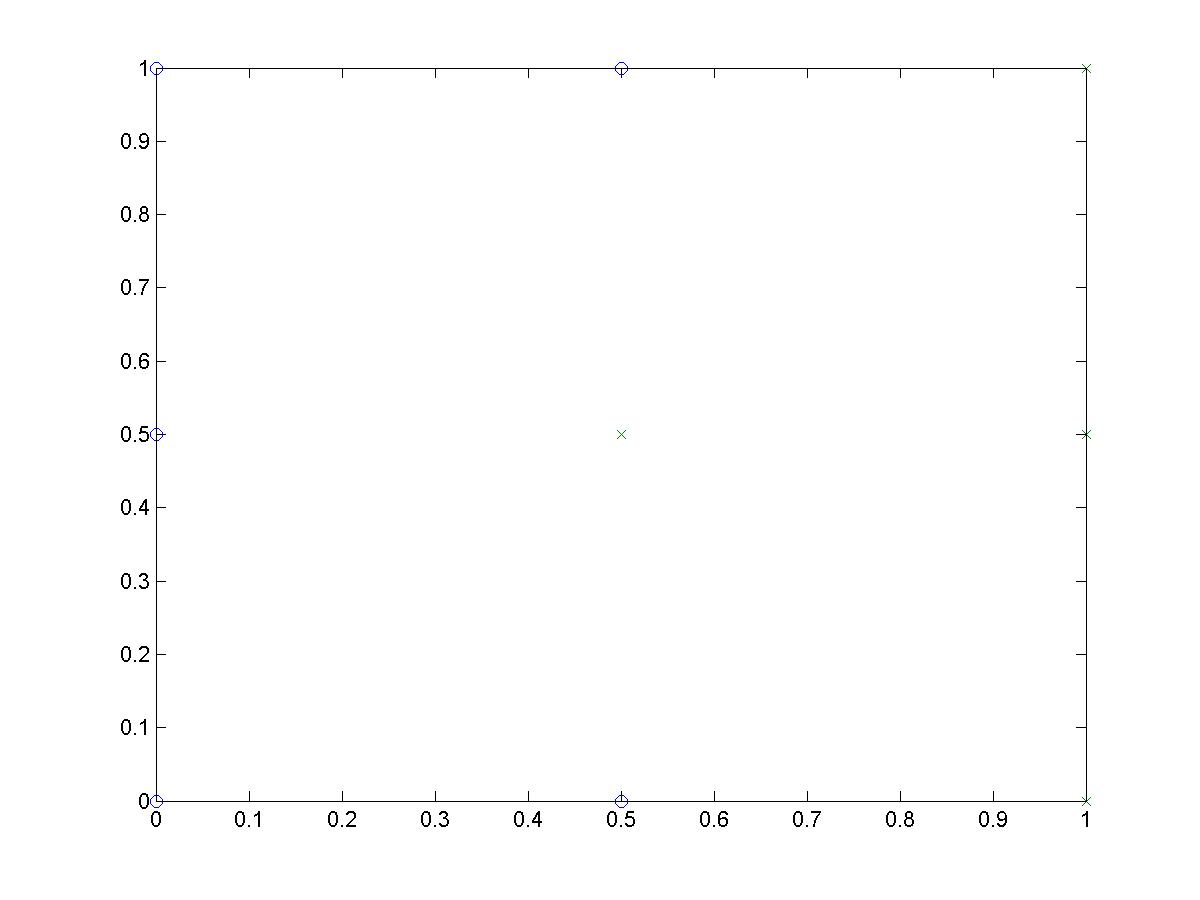
TWO LAYER PERCEPTION IMPLEMENTATION

The two layer perceptron intends to seperate non-linearly seperable sets that could not be solved using TLUs. This example seperates the problem shown below. The code shown below could be used to solve other non-linearly seperable problems. The code may also be adapted to include even higher layers of perceptrons. The following simulation was performed in Matlab. The Matlab file is available here: perceptron.m

function [W,dActual] = perceptron(x,d)
    alpha = 0.75;
    N = 50000;
    W = rand(3,3);

    for counter = 1:N
        index = mod(counter-1,size(x,2))+1;
        
        [y,z] = evaluatePerceptron(W,x(:,index));
        
        gradientE = zeros(3,3);
        for i = 1:2
            for j = 1:3
                gradientE(j,i) = -(d(index)-y)*y*(1-y)*W(i,3)*z(i)*(1-z(i))*x(j,index);
            end
        end
    
        for j = 1:3
            gradientE(j,3) = -(d(index)-y)*y*(1-y)*z(j);
        end
        
        W = W-alpha*gradientE;
    end

    dactual = zeros(size(d));
    for counter = 1:size(x,2)
        dActual(counter) = evaluatePerceptron(W,x(:,counter));
    end
   
    X = 0:0.01:1;
    Y = X;
    Z = zeros(length(Y),length(X));
    for i = 1:length(X)
        for j = 1:length(Y)
            Z(j,i) = evaluatePerceptron(W,[X(i);Y(j);-1]);
        end
    end
    mesh(X,Y,Z);
    view(-10,35);

    return
    
function f = sigmoid(v)
    f = 1/(1+exp(-v));
    
    return
    
function [y,z] = evaluatePerceptron(W,x)
    z = [sigmoid(W(:,1)'*x);sigmoid(W(:,2)'*x);-1];
    y = sigmoid(W(:,3)'*z);
    
    return

>> [W,d] = perceptron([0,0,0,0.5,0.5,0.5,1,1,1;0,0.5,1,0,0.5,1,0,0.5,1;
                       -1,-1,-1,-1,-1,-1,-1,-1,-1],[0,0,0,0,1,0,1,1,1])

W =

    9.4400    7.4031    6.4046
   -8.4903    6.7129    6.9753
   -1.7083    5.1559    9.7832


d =

    0.0131    0.0002    0.0177    0.1122    0.8852    0.1070    0.9493    0.9725    0.9599

Problem (click on image to view larger version)

Result (click on image to view larger version)