IRC TR 1997-061
Copyright 1997 Interval Research Corporation.
The research described in this technical report is summarized in Covell, Withgott, Slaney,
"Mach1: Nonuniform Time-Scale Modification
of Speech," Proc. IEEE International Conference on Acoustics,
Speech, and Signal Processing, Seattle WA, May 12-15 1998.
The description and analyses given here are more complete
than those within our ICASSP publication.
Mach1 for Nonuniform Time-Scale Modification of
Speech:
Theory, Technique, and Comparisons
Michele Covell, Margaret Withgott,1 and Malcolm Slaney
Interval Research Corporation
1801 Page Mill Road, Bldg. C
Palo Alto, CA 94304
Abstract
We propose a new approach to nonuniform time compression, called
Mach1, designed to mimic the natural timing of fast
speech. At identical overall compression rates, listener comprehension
for Mach1-compressed speech increased between 5 and 31 percentage
points2 over that
for linearly compressed speech, and response times dropped by 15%. For
rates between 2.5 and 4.2 times real time, there was no significant
comprehension loss with increasing Mach1 compression rates. In A-B
preference tests, Mach1-compressed speech was chosen 95% of the
time. This technical report describes the Mach1 technique and our
listener-test results. Audio examples can be found on http://www.interval.com/papers/1997-061/.
1 Linear Time Compression
Time-compression techniques change the playback rate of speech without introducing pitch artifacts. However, when linear compression techniques are used, human comprehension of time-compressed speech typically degrades at compression rates above two times real time [King89]. These degradations are not due to the speech rate per se: Comprehension of linearly compressed speech often breaks down above 225 to 270 words per minute (wpm) [Gade89], which is well below the rates at which long passages of natural speech are comprehensible (up to 500 wpm) [Fulford93].
Instead, the incomprehensibility of time-compressed speech is due to its unnatural timing. Mach1, described in Section 2, is an alternative to linear time compression. Mach1 compresses the components of an utterance to resemble closely the natural timing of fast speech. Section 3 describes our test of comprehension and preference levels for Mach1-compressed and linearly compressed speech. In Section 4, we draw our conclusions.
2 Mach1 Time Compression
Mach1 mimics the compression strategies that people use when they talk fast in natural settings. We used linguistic studies of natural speech [vanSanten94,Withgott93] to derive these goals:
- Compress pauses and silences the most
- Compress stressed vowels the least
- Compress schwas and other unstressed vowels by an intermediate amount
- Compress consonants based on the stress level of the neighboring vowels
- On average, compress consonants more than vowels
Also, to avoid obliterating very short segments, we want to avoid overcompressing already rapid sections of speech.
Unlike previous techniques [Arons94,Lee97], Mach1 deliberately avoids categorical recognition (such as silence detection and phoneme recognition). Instead, as illustrated in Figure 1, it estimates continuous-valued measures of local emphasis and relative speaking rate. Together, these two sequences estimate what we call audio tension: the degree to which the local speech segments resist changes in rate. High-tension segments are less compressible than low-tension segments. Based on the audio tension, we modify the target compression rate to give local target compression rates. We use these local target rates to drive a standard, time-scale modification technique (e.g., synchronized overlap-add [Roucous85]).
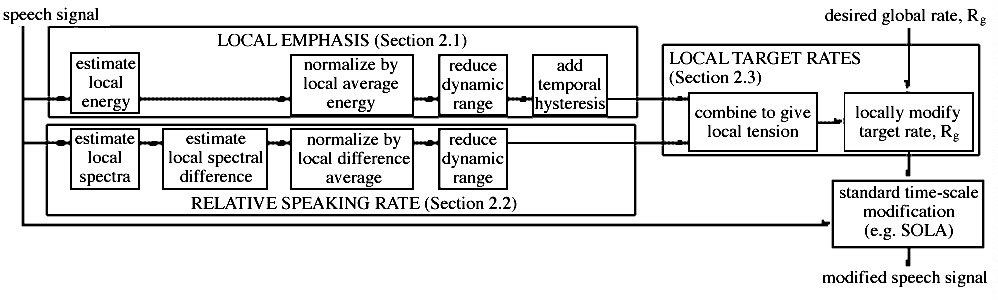 |
| Figure 1: Overview of Mach1. Mach1 first estimates the local emphasis and relative speaking rate. It then locally modifies the global target compression rate using a combination of those measures. The resulting locally varying target rate drives any standard time-scale modification technique. A larger version of this block diagram is linked to the in-line version. |
In Sections 2.1 through 2.3, we highlight important characteristics of the local-emphasis measure, of the relative speaking-rate measure, and of the technique used to combine them.
2.1 Local-Emphasis Measure
We use the local-emphasis measure to distinguish among silence, unstressed syllables, and stressed syllables. Emphasis in speech correlates with relative loudness, pitch variations, and duration [Chen92]. Of these, relative loudness is the most easily estimated. Reliable pitch estimation is notoriously difficult. Reliable duration estimation requires phoneme recognition, because natural durations are highly phoneme dependent. Instead, we rely on relative loudness to estimate emphasis.
Our method is explained here, in terms of both our general goal at each stage of the computation and our detailed (but often arbitrary) computational choices.
2.1.1 Estimating local energy
To estimate local emphasis, we first calculate the local energy. We simply use the frame energies from the spectrogram is used in speaking-rate estimation (see Section 2.2).
2.1.2 Normalizing by the local energy average
Emphasis is indicated more by relative loudness than by absolute loudness. So, we normalize our local energy by the local average energy.
We use a single-pole low-pass filter to estimate the average energy (tau = 1 sec). We then divide the local energy by the low-passed local energy.
2.1.3 Reducing the dynamic range
The variations of the local relative energy are not linearly related to our goal: controlling the segment-duration variations to mimic those seen in natural speech. In the data that we collected, the local relative energy within emphasized vowels averages around 4.4, with variations from 1.6 to as high as 40.3 The 95% confidence interval includes upward variations of 238% above the mean. In contrast, the relative variability of stressed-vowel durations observed in natural speech is closer to 22% [vanSanten92]. At the same time, the local-energy variations between unstressed vowels and pauses are less than the compression-rate variations for those segments seen in natural slow and fast speech [Stifelman97,vanSanten92].
Therefore, we estimate the frame emphasis by applying a compressive function to the relative energy. The compressive function reduces the dynamic range of the large-relative-energy segments (the emphasized vowels) and expands the dynamic range of the small-relative-energy segments (the unemphasized vowels and the pauses). Currently, our compressive function is hard limiting (to below 2) followed by a square-root function.
2.1.4 Adding temporal hysteresis
Speech perception and production include temporal grouping effects. In American English, all segments in stressed syllables tend to be less variable than those in unstressed syllables [Withgott93]. This observation implies that unvoiced consonants in a stressed syllable need to be treated as emphasized, even though their frame-emphasis values are low: The reduction of the consonants is controlled more by the stress of neighboring vowels than by the signal characteristics of the consonant itself.
Similar temporal-grouping effects are present during pauses within speech. The durations of long pauses (200 to 7000 msec) are much less stable than those of short pauses: Even after normalization for the mean durations, the standard deviation is 3.5 times higher for long pauses than for short [Stifelman97]. Long interphrase pauses can be reduced to 150 msec with little effect on comprehension [Arons94]. Below 100 to 150 msec, further interphrase pause compression causes false pitch-reset percepts.4 Thus, our intention is to treat silences near voiced speech as speech and to compress heavily or to remove completely silences outside of this range.
To account for these temporal grouping effects, we apply a tapered, temporal hysteresis to the frame emphasis to give our final local-emphasis estimates. Our hysteresis extends the influence of each frame-emphasis value by 80 msec into the past and 120 msec into the future. To minimize discontinuities in the local emphasis, we taper the hysteresis, using a triangle function to extend each frame-emphasis value into the past and future. We then find the maximum tapered future (or current) frame-emphasis value and the maximum tapered past (or current) frame-emphasis value. The local-emphasis value is the average of these two tapered maxima.
2.2 Relative Speaking-Rate Measure
We estimate the speaking rate to avoid overcompressing, and thereby obliterating, already rapid speech segments. True speaking rate is difficult to measure. We can, however, easily compute measures of acoustic-variation rates, which covary with speaking rate. Conceptually, we are using the phoneme-transition rate to estimate speaking rate: the higher the transition rate, the faster the speaking rate. By lowering our compression during transitions, we effectively lower the compression of rapid speech. This approach also has the advantage of preserving phoneme transitions, which are particularly important for human comprehension [Furui86,Stevens80]. In practice, we use relative acoustic variability, instead of transition labels, to modulate the compression rate, thereby avoiding categorical errors and simplifying the overall estimation process.
2.2.1 Estimating local spectra
Our estimate of relative acoustic variability starts with a local spectral estimate. We use the spectral values from a preemphasized narrow-band spectrogram, with a frame length of 20 msec and a step size of 10 msec.
To avoid unreliable estimates in low-energy regions, we set each frame
whose energy level is below a dynamic threshold to the previous
frame's values. Our dynamic threshold varies linearly with the local
energy average (described in Section
2.1.2); for the results reported here, we set the threshold such
that frames with energy levels below 4% of the
local average are reset.
2.2.2 Estimating local spectral difference
Intensity-discrimination studies [Moore95] suggest that human perception of acoustic change is closely approximated by log(1 + (delta I)/I), where I is intensity. We therefore use the sum of absolute log ratios between the current and the previous frames' values to estimate the local spectral difference.
To avoid overestimating the spectral difference due to simple (scalar) changes in loudness, we normalize each frame's values by that frame's total energy level prior to taking the absolute log ratios. To avoid overestimating the spectral difference due to unreliable values in low-energy frequency bins, we sum over the most energetic bins only. Currently, we sum over the bins within 40 dB of the maximum current-frame value.
2.2.3 Normalizing by the local spectral-difference average
Different speaking styles and different recording environments introduce wide deviations in our absolute spectral-difference measure. To avoid being unduly affected by these variables, we normalize our spectral difference by the local average difference.
Guided by informal listener tests, we estimate the local average difference using a weighted average. The average is weighted by the local-emphasis measure (computed in Section 2.1). To compute the weighted average efficiently, we apply a single-pole, low-pass filter (tau = 1 sec) to the emphasis-weighted spectral difference. The relative spectral difference is then the ratio of the local emphasis-weighted spectral difference to the emphasis-weighted average difference.
2.2.4 Reducing the dynamic range
The variations of the relative spectral difference overestimate the upward variations in relative speaking rate. The upper 1% of the weighted spectral-difference values range from 4 to 10 times the average. Most of the large relative spectral differences occur at plosive releases. In contrast, except for plosives, segmental-rate variations in natural speech remain below 4 times the average speaking rate [vanSanten92,vanSanten94]. Despite this exception, the large upward variations in the speaking-rate estimate should be eliminated: [vanSanten94] reports that, in naturally fast speech, the local reduction in compression during plosives is only about 20%.
Therefore, this step estimates the relative speaking rate by simply hard-limiting the relative spectral difference to below four times the average.
2.3 Local Target Compression Rates
The local-emphasis and relative speaking-rate measures depend purely on the audio signal that we plan to modify: They can be computed as the signal is being recorded. What remains is to combine these two measures together, to get a single measure of the compressibility of the underlying speech and to then combine that compressibility measure with the listener's target compression (or expansion) rate.
2.3.1 Computing audio tension
We compute audio tension from local emphasis and relative speaking rate using a simple linear formula:
g(t) = a ((E(t) - ME) + b(S(t) - MS)),
where
- g(t) is an audio-tension value
- E(t) is a local-emphasis estimate for the speech utterance being compressed
- S(t) is a relative speaking-rate estimate
- ME and MS are the mean values of the local-emphasis and speaking-rate estimates, respectively
- a > 0 is a constant-valued coefficient
- b is a constant-valued coefficient, with b > 0 for time compression and b < 0 for time expansion
Thus, the audio tension increases as the local emphasis increases, from low tension (comparatively large compressions or expansions) in regions of silence to high tension (comparatively small compressions or expansions) in stressed segments. For time compression, the audio tension increases as the relative speaking rate increases, from low tension (comparatively large compressions) in regions of slow speech to high tension (comparatively small compressions) in regions of fast speech. Due to the sign change of b, the opposite is true for time expansion: The audio tension decreases as the relative speaking rate increases, from high tension (comparatively small expansions) in regions of slow speech to low tension (comparatively large expansions) in regions of fast speech.
For the results reported here, we set a = 1/2 and b = 1/4. For simplicity, we set ME and MS to a prior estimate of the mean emphasis and speaking rate:5 Specifically, we set ME = 0.7 and MS = 1.0.
2.3.2 Computing local target compression rates
From audio tension and from a desired global compression (or expansion) rate, we compute local target rates as6
r(t) = max { 1, Rg + (1 - Rg) g(t)),
where
- r(t) is a local target compression or expansion rate
- Rg is the desired global compression or expansion rate
We use these target local compression rates as an input to standard time-scale modification techniques. With synchronous overlap-add (SOLA), for example, we use the local target rates to set, frame by frame, the target offset between the current and previous frames in the output audio signal.
The sequence of local compression (or expansion) rates typically gives overall compression (expansion) rates near the requested global rate, Rg. However, there is no guarantee that this global rate will be achieved. In cases where the global compression rate is important, we add a slow-response feedback loop around the previously described system. This feedback loop acts to correct long-term errors in the overall compression (expansion) rate by adjusting the nominal value of Rg appropriately. The loop's response time must be slow, to avoid distracting artifacts due to rapid changes in the target rate.
3 Comparison of Mach1-Compressed and Linearly Compressed Speech
We conducted a listener test comparing Mach1-compressed speech to linearly compressed speech. Parts of this test can be found on our web page (http://www.interval.com/papers/1997-061/).
3.1 Method
Fourteen subjects participated in a listener test to compare comprehension and preferences for Mach1-compressed versus linearly compressed speech. All the subjects were adult professionals, fluent in English and without hearing impairments. None had significant prior experience in listening to time-compressed speech. All aspects of the test, except the identity of the compression technique used on each clip, were explained to the subjects before testing.
All the test materials were taken from Kaplan's TOEFL study program [Rymniak97]: The utterances are from their audio CD and the questions and answer choices are from their book. We screened the utterances and the comprehension questions to remove those based on factual information (e.g., the physical characteristics of New York). The questions used in comprehension sections relate to information available from the audio samples only (e.g., a partial train schedule followed by "When does the 4 train make local stops?"). We created individual audio clips from CD tracks by segmenting out the desired utterances and including 0.25 second of silence at the beginning and end of each clip. Word counts for each audio clip were taken from the Kaplan-provided transcripts. The uncompressed audio samples range from 111 to 216 wpm.
Each audio clip was sped up twice: once using Mach1 compression and once using linear compression. Since all our audio was single pitched, we used SOLA both as the (variable-rate) Mach1-driven compression technique and as the (constant-rate) linear compression technique. The overall compression rates for the two techniques were equal.
Mach1 compression was done first, with Rg = 3, and without correction of the overall compression rate (Section 2.3.2). The true compression rate achieved by Mach1 on each audio sample was computed. Each clip was then recompressed linearly to the same global rate that the Mach1 compression achieved. This process gave two versions of each audio sample--one from Mach1, the other from linear compression--both with the same overall compression rate.
The actual compression rates that we achieved using this approach ranged between 2.56 and 4.15 times real time (mean=3.02, median=2.99, s.d.=0.35). The resulting speaking rate ranged from 390 to 673 wpm (mean=500, median=497, s.d.=57). As shown in the compression-wpm scatter plot of Figure 2, the resulting audio clips cover the rectangle from 420 to 600 wpm and from 2.6 to 3.5 compression rate.
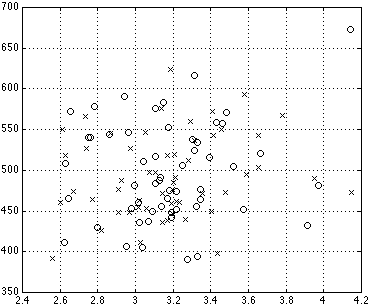 | Figure 2: Scatter plot of audio clips used in listener test. The two pools of audio data are distinguished by the x's and o's. A larger version of this scatter plot is linked to the in-line version.
(horizontal axis = compression rate; vertical axis = final wpm rate)
|
Each audio sample was assigned to pool A or to pool B. These audio pools were approximately balanced for compression-wpm rates. This balancing was done separately for each section of the test. (The individual test sections are given in Sections 3.1.1 to 3.1.4.) In the comprehension sections of the test, one half of the subjects heard the pool-A audio clips compressed with Mach1 and the pool-B audio clips compressed linearly. The other one half of the subjects heard the opposite technique: pool-A audio clips compressed linearly and pool-B audio clips compressed with Mach1. Assuming that the audio pools (and their associated questions) were correctly balanced for difficulty and that the two groups of subjects were also well balanced, this technique allows us to use purely within-subjects measures of the difference between Mach1 and linear compression. We tested for differences between the pools as part of our multivariate analysis of variance (MANOVA). No statistically significant differences were found (group effects: F1,12 = 0.03, p = 0.874; group X section effects: F4,9 = 0.52, p = 0.722; group X compression-type effects: F1,12 = 1.08, p = 0.319).
In the preference section, both Mach1-compressed and linearly compressed versions of the selected audio samples were played, allowing direct comparisons between the compression techniques. The presentation order of the audio (i.e., whether Mach1 was first) was again balanced relative to compression-word-per-minute rates.
The test was divided into six sections: Five sections tested comprehensibility of compressed audio clips; the final section tested preference between compression types.
3.1.1 Testing short-dialog comprehension
Three of the five comprehension sections were based on 90 short dialogs. Each dialog used one male and one female voice, saying one sentence each. Each audio clip also included one verbal question, spoken by a third voice, at the end of the dialog. Each audio clip (both dialog and question) was compressed as described previously.
Throughout the comprehension sections, the subjects controlled when the playback of each audio clip began, so they could to rest prior to starting each new audio clip without affecting their response-time data. Throughout the comprehension sections, the subjects had no control over the playback once it was started; each audio clip in the comprehension sections could be played once only.
Each question had to be answered with one of four answers. The choices were displayed on the screen after the audio clip finished playing. Throughout the comprehension sections, response times were measured from the time the answers appeared to the time the subjects submitted their answers. The subjects knew that their response times were being measured.
These short-dialog comprehension tests were presented to the subjects as the first, third, and fifth sections of the test.
3.1.2 Testing long-dialog comprehension
Another comprehension section was based on 10 long dialogs and 40 questions total. Each dialog used two voices (one male, one female); each voice spoke three to four times, saying 7 to 14 sentences. Each dialog was compressed as described previously.
After the dialog, four written questions and answers were shown to the subjects. Each question had to be answered from four forced-choice answers. The questions and answers were shown to the subjects sequentially, the first immediately after the audio clip finished playing and the following ones immediately after the previous question was answered.
These tests of long-dialog comprehension were presented to the subjects as the second section of the test.
3.1.3 Testing monolog comprehension
Another comprehension section was based on eight monologs and 30 questions total. Each monolog used one voice, saying 9 to 15 sentences. Each monolog was compressed as described previously.
After the monolog finished playing, three or four written questions and answers were shown to the subjects. The format was the same as that used for the long dialogs.
These monolog comprehension tests were presented to the subjects as the fourth section of the test.
3.1.4 Testing subjective preference
The preference section was based on 40 pairs of audio clips. Each pair of clips used either a dialog or a monolog from the previous comprehension sections. Each pair was compressed as described previously. In this section only, the subjects could control freely the playback of each pair of audio clips: They could play either audio clip as often as desired, they could switch back and forth between audio clips, and they could rewind either clip.
Once the subjects listened to at least part of each of the pair of audio clips, they could select one or the other clips as their preference. They were required to make a choice between all pairs of audio. Response times were not measured; instead, the subjects were encouraged to take as much time as they needed to decide between the clips.
This preference test was presented to the subjects as the sixth and final section of the test.
3.2 Results
We analyzed the results of the comprehension sections using a two-way, within-subjects MANOVA. The two treatment factors were two compression types (Mach1, linear) and five test sections (three short-dialog sections, one long-dialog section, one monolog section). The mean comprehension rate across all categories was 77%. The mean response time was 7.9 sec. The overall difference in comprehension rates between Mach1-compressed and linearly compressed speech was 17 ± 4 percentage points.2 The overall difference in response times between compression types was -1.2 sec ± 0.6 sec. These differences were clearly significant (F1,13 = 69.8, p < 0.001 for the comprehension differences; F1,13 = 17.8, p = 0.001 for the response-time differences). There was also significant interactions between compression type and test section (F4,10 = 13.6, p < 0.001 for the comprehension differences; F4,10 = 13.2, p = 0.001 for the response-time differences). The differences in comprehension rates between the compression types are shown by section in Table 1. We tested the significance of these differences individually using planned comparisons. The results of those tests are also included in Table 1.7
| Table 1: Comprehension-rate differences between Mach1-compressed and linearly compressed speech, by test section. Significance levels for each section are also shown.
|
| Section type | Compression (in percentage points) |
| Average | Difference (Mach1 - linear) |
| short dialogs | 70 | 31.0 (t'52 = 8.60, p < 0.001) |
| 82 | 14.8 (t'52 = 4.13, p < 0.001) |
| 76 | 24.3 (t'52 = 6.79, p < 0.001) |
| long dialogs | 79 | 5.4 (t'52 = 1.50, p = 0.702) |
| monologs | 81 | 10.0 (t'52 = 2.79, p = 0.036) |
We also did a regression analysis of the question-by-question comprehension rates (averaged across subjects) versus compression rate. As expected, with linearly compressed speech, comprehension fell with increased compression: slope m = -0.26,8 correlation coefficient r = -0.32;9 t158 = 4.20, p < 0.001. In contrast, with Mach1-compressed speech, there was no significant comprehension loss with increased compression. Furthermore, the difference in comprehension rates between Mach1-compressed and linearly compressed speech increased with increasing compression rate: m = 0.34, r = 0.42; t158 = 5.81, p < 0.001 (Figure 3). There were no statistically significant correlations between comprehension and speaking (wpm) rate.
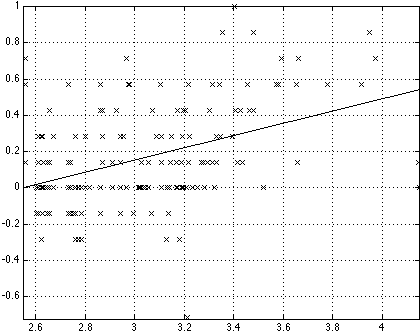 | Figure 3: Plot of difference in comprehension between Mach1 and linear compression as a function of compression rate. The results of linear regression are shown as a solid line. A larger version of this plot is linked to the in-line version.
(horizontal axis = compression rate; vertical axis = difference in comprehension) |
In the preference section, Mach1-compressed speech was chosen 94.8% of the time over linearly compressed speech, for identical global compression rates. This preference rate is clearly different from random selection (t12 = 21.9, p < 0.001). There was a positive correlation between compression rate and Mach1 preference rate: m = 0.10, r = 0.56, t38 = 4.76, p < 0.001 (Figure 4). There was no statistically significant correlation between Mach1 preference rate and the corresponding speaking rates.
 | Figure 4: Plot of Mach1 preference rate as a function of compression rate. The results of linear regression are shown as a solid line. A larger version of this plot is linked to the in-line version.
(horizontal axis = compression rate; vertical axis = Mach1 preference rate) |
4 Conclusions
Mach1 offers significant improvements in comprehension over linear compression, especially at high compression rates: Comprehension improved by 17 percentage points when Mach1 was used instead of linear compression, at the same global rates. The difference in comprehension rates between Mach1-compressed and linearly compressed speech increased with increasing compression rate. Listeners preferred Mach1-compressed speech over linearly compressed speech 95% of the time. The preference for Mach1 increased with increasing compression rate.
Short dialogs provided the greatest improvement in comprehension, averaging 23 percentage points. The comprehension improvements were less with the longer clips: 10 percentage points with monologs and 5 percentage points with long dialogs. The large comprehension improvements on short dialogs was due mostly to lowered comprehension of the linearly compressed speech. Since the short dialogs (averaging 23 words) are significantly shorter than the other clips (averaging 144 and 187 words for the long dialogs and monologs), one possible explanation for the lower comprehension of the linearly compressed short dialogs is that the most information is lost at the beginning of the clips, while the subjects adjust to the unnatural speaking style. The absence of a similar decrease in comprehension of Mach1-compressed short dialogs suggests that the listener-adjustment period is much shorter when Mach1 is used.
The comprehension improvements with Mach1 were statistically significant for short dialogs and for monologs. The improvement for long dialogs was not statistically significant. This failure to attain statistical significance may be due to the small test population. Another possibility is there may be confusing interactions between Mach1 and the turn-taking techniques used in conversation. These interactions could have been masked in the short dialogs by the heavily reduced comprehension of linearly compressed speech.
It is interesting to note that, with Mach1 compression, there was no statistically significant loss in comprehension as a function of compression rate.10 One hypothesis for the uniform comprehension results across achieved compression rates is that Mach1 is doing a fairly good job of capturing the relative compressibility of each audio clip in the audio tension. Mach1 itself determined the distribution of compression rates: it was given a nominal compression target of 3 times real time but was allowed to deviate from that target according to the results of the audio tension calculations on each clip. In some sense, Mach1 may be providing "a predictable overall comprehensibility" instead of providing "a predictable overall compression rate".
Variable-rate compression of speech is a promising direction in time-scale modification. It should allow us to improve our comprehension rates using approaches suggested by linguistic and text-to-speech studies. It leaves open the question of how best to measure paralinguistic qualities, such as emphasis and relative speaking rate. The Mach1 approach avoids categorical labels and relies on easily measurable acoustic correlates. This approach has proved fruitful, conferring significant improvements in comprehension over linear compression.
Acknowledgments
We thank Gerald McRoberts and Dan Levitin for their advice on designing the listener test, Jennifer Orton for running the listener tests, Jennifer Smith for her guidance and work in statistical analysis, and Tom Ngo and Lyn Dupré for their editing advice. We also thank all our listener-test subjects who gave us an hour of their time and attention, so that we could test our approach.
References
B. Arons, 1994. "Interactively Skimming Recorded Speech," Ph.D. dissertation, Massachusetts Institute of Technology, Boston, MA.
F. Chen, M. Withgott, 1992. "The Use of Emphasis to Automatically Summarize a Spoken Discourse," IEEE International Conference on Acoustics, Speech and Signal Processing, Vol. 1, pp 229-232, San Francisco, CA.
C. Fulford, 1993. "Can Learning be more Efficient? Using Compressed Audio Tapes to Enhance Systematically Designed Text," Educational Technology, 33(2): 51-59.
S. Furui, 1986. "On the Role of Spectral Transition for Speech Perception," Journal of the Acoustical Society of America, 80(4): 1016-1025.
P. Gade, C. Mills, 1989. "Listening Rate and Comprehension as a Function of Preference for and Exposure to Time-Altered Speech," Perceptual and Motor Skills, 68(2): 531-538, 1989.
D. Howell, 1992. Statistical Methods for Psychology, Duxbury Press, Belmont, CA.
P. King, R. Behnke, 1989. "The Effect of Time-Compressed Speech on Comprehensive, Interpretive, and Short-Term Listening," Human Communication Research, 15(3): 428-443.
S. Lee, H. Kim, et al., 1997. "Variable Time-Scale Modification of Speech Using Transient Information," IEEE International Conference on Acoustics, Speech, and Signal Processing, Vol. 2, pp 1319-1322, Munich.
B. Moore, 1995. Hearing, Academic Press, San Diego, 1995.
S. Roucous, A. Wilgus, 1985. "High Quality Time-Scale Modification for Speech," IEEE International Conference on Acoustics, Speech, and Signal Processing, Vol. 2, pp 493-496, Tampa, FL.
M. Rymniak, G. Kurlandski, et al., 1997. The Essential Review: TOEFL (Test of English as a Foreign Language), Kaplan Educational Centers and Simon & Schuster, New York.
K. Stevens, 1980. "Acoustic Correlates of Some Phonetic Categories," Journal of the Acoustical Society of America, 68(3): 836-842.
L. Stifelman, 1997. "The Audio Notebook: Paper and Pen Interaction with Structured Speech," Ph.D. dissertation, Massachusetts Institute of Technology, Boston, MA.
J. van Santen, 1992. "Contextual effects on vowel duration," Speech Communication, 11(6): 513-546.
J. van Santen, 1994. "Assignment of Segmental Duration in Text-to-Speech Synthesis," Computer Speech and Language, 8(2): 95-128.
M. Withgott, F. Chen, 1993. Computational Models of American Speech, CSLI Lecture Notes #32, Center for the Study of Language and Information, Stanford, CA.
1.
Meg Withgott is currently affiliated with Electric Planet; 3200 Ash; Palo Alto, CA 94306 (phone: 650 812-0112; fax: 650 842-0368; e-mail: mwithgott@e-planet.com).
2.
There is an ambiguity in percentage change in comprehension rates. To illustrate this problem, consider the case in which the comprehension rate of Mach1-compressed speech is 90% and the comprehension rate of linearly compressed speech is 60%. This difference in comprehension could be described as an increase of 50% ((0.9-0.6)/0.6 = 50%) or as an increase of 30 percentage points (90%-60% = 30%). To avoid this confusion, we report all changes in comprehension in terms of percentage points: the preceding example would be reported as 30 percentage points. To emphasize this convention, we spell out "percentage points" in those cases that would otherwise be ambiguous.
3.
This large upward variation largely results from the depression in the local average at the beginning of each new sentence, due to a pause between sentences and to a downward energy tilt across the preceding sentence.
4.
Pitch resets are perceived as sudden discontinuities in the pitch contour, usually indicating a change of speaker or topic. While the pitch may change drastically from one sentence to the next, if the interphrase pause is naturally long, it is perceived as a continuous variation, instead of as a pitch reset. Only when the pause is artifically shortened is the false percept introduced.
5.
These prior estimates of ME and MS were derived from a set of speech samples that did not include any of the samples used in the listener tests, discussed in Section 3.
6.
In this equation for r(t), we assume that both compression and expansion rates are expressed as numbers greater than 1. Using this convention, the offset between time frames of the output is set to 1/r(t) times the input frame offset for compression, and is set to r(t) times the input frame offset for expansion.
7.
The probabilities reported in Table 1 use the Bonferroni t' distribution [Howell92] for the five planned comparisons: They are five times higher than would be given by the unmodified t distribution.
8.
This slope value, m = -0.26, means that, on average, there was 26% less comprehension at each unit increase of compression.
9.
The correlation-coefficient estimate, r, is tested for significance using sqrt((1 - r2) / (N - 2)) as its standard error [Howell92].
10.
In fact, there was a slight increase in comprehension for the higher compression rates: m = 0.08. However, the correlation coefficient for this increasing trend, r = 0.14, was not statistically signficant (t158 = 1.76, p = 0.08).




