This is a reprint of a paper that was published in the Proceedings of the 1997 International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Munich, Germany, April 21-24, 1997. Copyright 1997, IEEE. Postscript and PDF copies of this paper are also available.

Personal use of this material is permitted. However, permission to reprint/republish this material for advertising or promotional purposes or for creating new collective works for resale or redistribution to servers or lists, or to reuse any copyrighted component of this work in other works, must be obtained from the IEEE. Contact: Manager, Copyrights and Permissions / IEEE Service Center / 445 Hoes Lane / P.O. Box 1331 / Piscataway, NJ 08855-1331, USA. Telephone: + Intl. 908-562-3966.

Construction and Evaluation of a Robust Multifeature Speech/Music Discriminator

Eric Scheirer - Malcolm Slaney
Interval Research Corporation
Palo Alto, CA 94304

Abstract:

We report on the construction of a real-time computer system capable of distinguishing speech signals from music signals over a wide range of digital audio input. We have examined 13 features intended to measure conceptually distinct properties of speech and/or music signals, and combined them in several multidimensional classification frameworks. We provide extensive data on system performance and the cross-validated training/test setup used to evaluate the system. For the datasets currently in use, the best classifier classifies with 5.8% error on a frame-by-frame basis, and 1.4% error when integrating long (2.4 second) segments of sound.

Overview

The problem of distinguishing speech signals from music signals has become increasingly important as automatic speech recognition (ASR) systems are applied to more and more ``real-world'' multimedia domains. If we wish to build systems that perform ASR on soundtrack data, for example, it is important to be able to distinguish which segments of the soundtrack contain speech.

There has been some previous work on this topic [1], [2]. Some of this work has suggested features which prove valuable for incorporation into a multidimensional framework, and we have included them when possible. This paper extends that work in several ways: by considering multiple features, by examining powerful classification methods, and by describing a principled approach to training and testing the system.

The rest of our paper is divided into three sections: a description of the features examined in our system; a discussion of the different multivariate classification frameworks which we have evaluated; and results of a careful training and evaluation phase in which we present the performance characteristics of the system in its current state.

Features

Thirteen features have been evaluated for use in the system. Each of them was intended to be a good discriminator on their own; as we shall show, not all of them end up adding value to a multivariate classifier. Of the thirteen, five are ``variance'' features, consisting of the variance in a one-second window of an underlying measure which is calculated on a single frame. If a feature has the property that it gives very different values for voiced and unvoiced speech, but remains relatively constant within a window of musical sound, then the variance of that feature will be a better discriminator than the feature itself.

It is also possible that other statistical analyses of ``underlying'' features, such as second or third central moments, skewness, kurtosis, and so forth, might make good features for discriminating classes of sound. For example, Saunders [2] bases four features on the zero-crossing rate, using the variance of the derivative, the third central moment, the thresholded value, and a skewness measure.

The features used in this system are:

• 4 Hz modulation energy: Speech has a characteristic energy modulation peak around the 4 Hz syllabic rate [3]. We use a portion of the MFCC algorithm [4] to convert the audio signal into 40 perceptual channels. We extract the energy in each band, bandpass filter each channel with a second order filter with a center frequency of 4 Hz, then calculate the short-term energy by squaring and smoothing the result. We normalize each channel's 4 Hz energy by the overall channel energy in the frame, and sum the result from all channels. Speech tends to have more modulation energy at 4Hz than music does.
• Percentage of ``Low-Energy'' Frames: The proportion of frames with RMS power less than 50% of the mean RMS power within a one-second window. The energy distribution for speech is more left-skewed than for music--there are more quiet frames--so this measure will be higher for speech than for music [2].
• Spectral Rolloff Point: The 95th percentile of the power spectral distribution. This measure distinguishes voiced from unvoiced speech--unvoiced speech has a high proportion of energy contained in the high-frequency range of the spectrum, where most of the energy for unvoiced speech and music is contained in lower bands. This is a measure of the ``skewness'' of the spectral shape--the value is higher for right-skewed distributions.
• Spectral Centroid: The ``balancing point'' of the spectral power distribution. Many kinds of music involve percussive sounds which, by including high-frequency noise, push the spectral mean higher. In addition, excitation energies can be higher for music than for speech, where pitch stays in a fairly low range. This measure gives different results for voiced and unvoiced speech.
• Spectral ``Flux'' (Delta Spectrum Magnitude): The 2-norm of the frame-to-frame spectral amplitude difference vector, 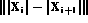. Music has a higher rate of change, and goes through more drastic frame-to-frame changes than speech does; this value is higher for music than for speech. Note that speech alternates periods of transition (consonant - vowel boundaries) and periods of relative stasis (vowels), where music typically has a more constant rate of change. This method is somewhat similar to Hawley's, which attempts to detect harmonic continuity in music [1].
• Zero-Crossing Rate: The number of time-domain zero-crossings within a speech frame [2]. This is a correlate of the spectral centroid. Kedem [5] calls it a measure of the dominant frequency in a signal.
• Cepstrum Resynthesis Residual Magnitude: The 2-norm of the vector residual after cepstral analysis, smoothing, and resynthesis. If we do a real cepstral analysis [6] and smoothing of the spectrum, then resynthesize and compare the smoothed to unsmoothed spectrum, we'll have a better fit for unvoiced speech than for voiced speech or music, because unvoiced speech better fits the homomorphic single-source-filter model than music does. In the voiced speech case, we are filtering out the pitch ``ripple'' from the signal, giving higher values for the residual.
• Pulse metric: A novel feature which uses long-time band-passed autocorrelations to determine the amount of ``rhythmicness'' in a 5-second window. It does a good job telling whether there's a strong, driving beat (ie, techno, salsa, straightahead rock-and-roll) in the signal. It can't detect rhythmic pulse in signals with rubato or other tempo changes.

  The observation used is that strong beat leads to broadband rhythmic modulation in the signal as a whole. That is, no matter what band of the signal you look in, you see the same rhythmic regularities. So the algorithm divides the signal into six bands and finds the peaks in the envelopes of each band; these peaks correspond roughly to perceptual onsets. We then look for rhythmic modulation in each onset track using autocorrelations, and select the autocorrelation peaks as a description of all the frequencies at which we find rhythmic modulation in that band.

  We compare band-by-band to see how often we find the same pattern of autocorrelation peaks in each. If many peaks are present at similar modulation frequencies across all bands, we give a high value for the pulse metric.

We use the variances of the rolloff point, spectral centroid, spectral flux, zero-crossing rate, and cepstral resynthesis residual magnitude as features as well. In practice, we are using log transformations on all thirteen features; this has been empirically determined to improve their spread and conformity to normal distributions. As an example, Figure 1 shows two of the features and their two-dimensional joint distribution. As we can see, there is significant overlap in the marginal probability distributions, but much less when the features are considered in conjunction.

   
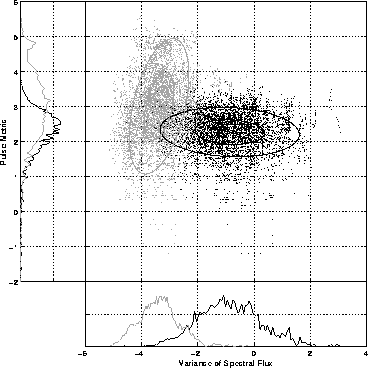
Figure 1: Marginal and joint probability distributions for two of the features examined in the system. The darker density cloud and histogram outline represent speech data; the lighter, music data. The ellipses are contours of equal Mahalanobis distance at 1 and 2 standard deviations. The data shown are a random sample of 20% of the training data. Each axis has been log-transformed.

Classification frameworks

We have examined a multidimensional Gaussian maximum a posteriori (MAP) estimator, a Gaussian mixture model classification, a spatial partitioning scheme based on k-d trees, and a nearest-neighbor classifier in depth. We will describe them here and contrast the way they divide the feature space; we will provide data for performance comparison in the Evaluation section.

Multidimensional MAP Gaussian classification works by modeling each class of data, speech and music, as a Gaussian-shaped cluster of points in feature space (for example, the 13-dimensional space consisting of the parameters described above). We form estimates of parameter mean and covariances within each class in a supervised training phase, and use the resulting parameter estimates to classify incoming samples based on their proximity to the class means using a Mahalanobis, or correlational, distance measurement.

A Gaussian mixture model (GMM) models each class of data as the union of several Gaussian clusters in the feature space. This clustering can be iteratively derived with the well-known EM algorithm [7]. In contrast to the MAP classifier, the individual clusters are not represented with full covariance matrices, but only the diagonal approximations. That is, the resulting Gaussian ``blobs'' have their axes oriented parallel to the axes of the feature space.

Classification using the GMM uses a likelihood estimate for each model, which measures how well the new data point is modeled by the entrained Gaussian clusters. An incoming point in feature space is assigned to whichever class is the best model of that point (whichever class the point is most likely to have come from).

The nearest-neighbor estimator simply places the points of the training set in feature space. To classify new points, we examine the local neighborhood of feature space to determine which training point is closest to the test point, and assign the class of this ``nearest neighbor''. Spatial partitioning schemes [8] are often used to make more efficient the process of determining which point in the training is the closest; we are using the k-d tree algorithm.

We have also investigated several common variants of the simple nearest-neighbor framework. The k-nearest-neighbor classifier conducts a class vote among the nearest k neighbors to a point; what we call k-d spatial classification approximates the k-nearest-neighbor approach by voting only among those training points in the particular region of space grouped together by the k-d tree partitioning. These points are nearby each other, but are not necessarily strictly the closest neighbors. This approximate algorithm is much faster than the true nearest-neighbor schemes.

The difference between the power of these classification schemes is obvious when the partition boundaries are considered. The Gaussian model creates a hyper-quadric surface boundary in the feature space (ie, hypersphere, hyperellipsoid, hyperparaboloid, etc). The Gaussian mixture model induces a decision boundary of a union of hyper-quadrics, where each hyper-quadric is oriented with the axes of the feature space.

The k-d spatial partitioning draws arbitrary ``Manhattan segment'' decision boundaries, whose complexity depends on the amount of training data and number of partitioning ``bins''. The nearest-neighbor and k-nearest schemes are attempting to estimate the local probability density within every area of the feature space, and so arbitrarily complex decision boundaries can be drawn, depending on the manifold topology of the training data.

Returning to Figure 1, we can see that Gaussians (or, perhaps, the union of a small number of Gaussians) are not a bad model for the individual features, but the joint distribution is not so easily described. In particular, there are clear locations in space where the data distribution is somewhat homogeneous--for example, near the point (-1,3.5) on the scatter plot--that do not fall into the main cluster regions.

We can estimate theoretical bounds on the performance of some classifiers. The estimated class assignment probability density 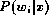given by the nearest-neighbor rule is no greater than 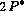, where is the underlying probability (see [9] p.100-102 for details on this derivation). This bound tells us that no matter what classifier we use, we can never do better than to cut the error rate in half over the nearest-neighbor classifier (and, in fact, the k-nearest-neighbor method is even more strictly bound), assuming our testing and training data are representative of the underlying feature space topology. Any further improvements have to come from using better features, more or better training data or by adding higher-level knowledge about the long-term behavior of the input signal.

Training, Testing, and Evaluation

We evaluated the models using labeled data sets, each 20 minutes long, of speech and music data. Each set contains 80 15-second-long audio samples. The samples were collected by digitally sampling an FM tuner (16-bit monophonic samples at a 22.05 kHz sampling rate), using a variety of stations, content styles, and noise levels, over a three-day period in the San Francisco Bay Area.

We made a strong attempt, especially for the music data, to collect a data set which represented as much of the breadth of available input signals as possible. Thus, we have both male and female speakers, both ``in the studio'' and telephonic, with quiet conditions and with varying amounts of background noise in the speech class; and samples of jazz, pop, country, salsa, reggae, classical, various non-Western styles, various sorts of rock, and new age music, both with and without vocals, in the music class.

For each classification model and several different subsets of features, we used a cross-validated testing framework to evaluate the classification performance. In this method, 10% (4 min.) of the labeled samples, selected at random are held back as test data, and a classifier trained on the remaining 90% (36 min.) of the data. This classifier is then used to classify the test data, and the results of the classification are compared to the labels to determine the accuracy of the classifier. By iterating this process several times and evaluating the classifier based on the aggregate average, we can ensure that our understanding of the performance of the system is not dependent on the particular test and training sets we have used.

Note that we are selecting or holding back blocks of points corresponding to whole audio samples; the frames from a single speech or music case will never be split into partially training and partially testing data. This is important since there is a good deal of frame-to-frame correlation in the sample values, and so splitting up audio samples would give an incorrect estimate of classifier performance for truly novel data.

We have used this cross-validation framework to evaluate the univariate and multivariate classification performance of the various models. The results are shown in Tables 1 and 2 respectively.

In Table 1, ``latency'' refers to the amount of past input data required to calculate the feature. Thus, while the zero-crossing rate can be calculated on a frame-by-frame basis, the variance of the zero-crossing rate is referring to the last second of data. The frame rate was 50 Hz for the performance measures shown here. The effect of varying the frame size and window overlap on classification performance has not been examined, but is not expected to be large. The error rates are calculated using a spatial partitioning classifier.

Feature	Latency	CPU Time	Error
4 Hz Mod Energy	1 sec	18%	12 +/-1.7%
Low Energy	1 sec	2%	14 +/-3.6%
Rolloff	1 frame	17%	46 +/- 2.9%
Var Rolloff	1 sec	17%	20 +/- 6.4%
Spec Cent	1 frame	17%	39 +/- 8.0%
Var Spec Cent	1 sec	17%	14 +/- 3.7%
Spec Flux	1 frame	17%	39 +/- 1.1%
Var Spec Flux	1 sec	17%	5.9 +/- 1.9%
Zero-Cross Rate	1 frame	0%	38 +/- 4.6%
Var ZC Rate	1 sec	3%	18 +/- 4.8%
Ceps Resid	1 frame	46%	37 +/- 7.5%
Var Ceps Res	1 sec	47%	22 +/- %5.7
Pulse Metric	5 sec	38%	18 +/- %2.9

 
Table 1:   Latency, CPU time required, and univariate discrimination performance for each feature. Each data point represents the mean and standard deviation of the proportion of frames misclassified over 10 cross-validated training runs. See text for details on testing procedure. CPU time is proportion of ``real time'' a feature takes for processing on a 120MHz R4400 Silicon Graphics Indy workstation. Note that many features can share work when classifying multidimensionally, so the total CPU time required is nonadditive.

 

Framework	Speech Error	Music Error	TotalError
MAP G'ss'n	2.1 +/- 1.2%	9.9 +/- 5.4%	6.0 +/- 2.6 %
GMM: 1 G	3.0 +/- 1.1%	8.7 +/- 6.6%	5.8 +/- 2.9 %
5 G	3.2 +/- 1.1%	8.4 +/- 6.8%	5.8 +/- 2.9 %
20 G	3.4 +/- 1.5%	7.7 +/- 6.2%	5.6 +/- 2.4 %
50 G	3.0 +/- 1.4%	8.2 +/- 6.6%	5.6 +/- 2.6 %
k NN: k=1	4.3 +/- 1.7%	6.6 +/- 6.4%	5.5 +/- 3.6 %
k=5	4.2 +/- 1.8%	6.4 +/- 6.2%	5.3 +/- 3.5 %
k=11	4.2 +/- 1.9%	6.5 +/- 6.1%	5.4 +/- 3.5 %
k=25	4.2 +/- 1.9%	6.5 +/- 6.1%	5.4 +/- 3.5 %
k-d: $b=5	5.2 +/- 1.0%	6.1 +/- 2.5%	5.7 +/- 1.5 %
b=11	5.4 +/- 1.1%	6.1 +/- 2.8%	5.8 +/- 1.6 %
b=21	5.7 +/- 1.4%	5.9 +/- 2.9%	5.8 +/- 1.9 %
b=51	5.9 +/- 1.8%	5.5 +/- 2.7%	5.7 +/- 2.0 %
b=101	6.1 +/- 1.7%	5.3 +/- 2.6%	5.7 +/- 1.8 %

 
Table 2: Performance (mean and standard deviation frame-by-frame error) for various multidimensional classifiers. For the k-d spatial classifier, the b parameter is the number of data points in the ``leaves'' of the data structure, and thus the spatial resolution of the classifier. A higher b value represents larger bins, and more samples to vote among in each bin. Note that GMM with one Gaussian is not the same as MAP, as GMMs use diagonalized covariances only.

In Table 2, performance differences between the classifiers and the effects of parameter settings for the parameterized classifiers are examined. For the k-nearest-neighbor classifiers, we varied the number of neighbors involved in the voting. For the k-d spatial classification procedure, we varied the number of data points collected in each data ``bucket'' or ``leaf''. Thus, higher values of b partition the feature space into broader groups. For the Gaussian mixture model classifier, we varied the number of Gaussians in each class.

Several results are apparent upon examination of Table 2. First, there is very little difference between classifiers, or between parameter settings for each classifier type. This suggests that the topology of the feature space is rather simple, and indicates the use of a computationally simple algorithm such as spatial partitioning for use in implementations. Second, it is generally more difficult to classify music than to classify speech; that is, it is easier to avoid mistaking music for speech than to avoid mistaking speech for music. This is not unexpected, as the class of music data, in the world and in our data set, is much broader than the class of speech samples.

Further, some of the classifiers differ in their behavior on the individual speech and music classes. For example, the MAP Gaussian classifier does a much better job rejecting music from the speech class than vice-versa, while the k-d spatial classifier with medium-sized buckets has nearly the same performance on each class. Thus, the different classifiers might be indicated in situations with different engineering goals.

We also tested several feature subsets using the spatial partitioning classifier; the results are summarized in Table 3. The ``best 8'' features are the variance features, plus the 4 Hz modulation, low-energy frame percentage, and pulse metric. The ``best 3'' are the 4 Hz energy, variance of spectral flux, and pulse metric. The ``fast 5'' features are the 5 basic features which look only at a single frame of data, and thus have low latency.

We can see from these results that not all features are necessary to perform accurate classification, and so a real-time system may gain improved performance by using only some of the features.

We can understand more fully the behavior of the algorithm by examining the distribution of errors. Figure 2 shows the classifications of test frames for one training/test partitioning. A number of features are apparent in this plot. First, there is a trial-by-trial difference; some samples are easy to classify, and some hard. This is true of both the speech region and the music region. Second, the errors are not independently distributed; they occur in long ``runs'' of misclassified frames. Finally, there are many more errors made in the early startup (frames 1-50), before the variance features can be collected, than in the later regions.

 

 
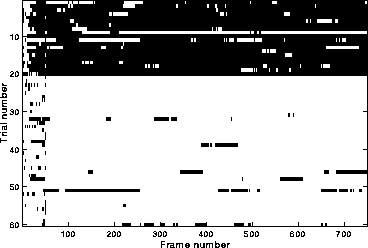
Figure 2: Classifications by trial and frame for one training/test partitioning of the data set. Each white point is a frame classified as music; each black point is a frame classified as speech. The trials in the upper region (trials 1-20) correspond to speech samples (although the classifier doesn't know); the bottom trials are music. Trials 9 and 11 are speech with background music and were not used in the other experiments. The high error rate in the first 50 frames is due to the use of low-latency features only.

  

Subset	Speech Error	Music Error	Total Error
All features	5.8 +/- 2.1 %	7.8 +/- 6.4 %	6.8 +/- 3.5 %
Best 8	6.2 +/- 2.2 %	7.3 +/- 6.1 %	6.7 +/- 3.3 %
Best 3	6.7 +/- 1.9 %	4.9 +/- 3.7 %	5.8 +/- 2.1 %
VSFlux only	12 +/- 2.2 %	15 +/- 6.4 %	13 +/- 3.5 %
Fast 5	33 +/- 4.7 %	21 +/- 6.6 %	27 +/- 4.6 %

Table 3: Performance (mean and standard deviation frame-by-frame error) for various subsets of features. The k-d spatial classifier was used in all cases. The ``Var Spec Flux only'' data is not directly comparable to that in Table 1, since in Table 1 ``cannot classify'' points were ignored, but here they are treated as errors.

Finally, for comparison with results reported previously [2], we calculated a long-term classification by averaging the results of the frame-by-frame spatial partitioning classification in nonoverlapping 2.4 second windows. Using this testing method, the error rate drops to 1.4%. Thus, the frame-by-frame errors, while not distributed independently, are separate enough that long-term averaging can eliminate many of them.

Conclusion

The multidimensional classifiers we have built provide excellent and robust discrimination between speech and music signals in digital audio. We note especially that the performance results presented are causal error, and so segmentation performance, where we know a priori that there are long stretches of alternating speech and music, would be significantly higher.

There are many interesting directions in which to continuing pursuing this work. For example, a simple three-way classifier using this feature set to discriminate speech, music, and simultaneous speech and music provided only about 65% accurate performance. Also, it does not seem as though this feature set is adequate to distinguish among genres of music. More research is needed on the methods humans use to solve these sorts of classification problems, and how to best implement those or other strategies in pattern-recognition systems.

References

1

Michael Hawley. Structure out of Sound. PhD thesis, MIT Media Laboratory, 1993.

2

John Saunders. Real time discrimination of broadcast speech/music. In Proc. 1996 ICASSP, pages 993-996, 1996.

3

T. Houtgast and H. J. M. Steeneken. The modulation transfer function in room acoustics as a predictor of speech intelligibility. Acustica, 28:66-73, 1973.

4

M. J. Hunt, M. Lennig, and P. Mermelstein. Experiments in syllable-based recognition of continuous speech. In Proc. 1980 ICASSP, pages 880-883, 1980.

5

Benjamin Kedem. Spectral analysis and discrimination by zero-crossings. Proc. IEEE, 74(11):1477-1493, 1986.

6

B. P. Bogert, M. J. R. Healy, and J. W. Tukey. The Quefrency Alanysis of Time Series for Echoes: Cepstrum, Pseudo-autocovariance, Cross-Cepstrum, and Saphe Cracking, pages 209-243. John Wiley and Sons, New York, 1963.

7

Todd K. Moon. The expectation-maximation algorithm. IEEE Signal Processing Magazine, pages 47-70, Nov. 1996.

8

Stephen M. Omohundro. Geometric learning algorithms. Technical Report 89-041, International Computer Science Institute, Berkeley CA, 1989.

9

Richard O. Duda and Peter E. Hart. Pattern Classification and Scene Analysis. John Wiley and Sons, New York, 1973.

...Scheirer

Eric Scheirer is currently at the MIT Media Laboratory, Cambridge, MA, USA, eds@media.mit.edu

...Slaney

Malcolm Slaney can be reached at malcolm@interval.com

About this document ...

Construction and Evaluation of a Robust Multifeature Speech/Music Discriminator

This document was generated using the LaTeX2HTML translator Version 96.1-h (September 30, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.