In-lab
Check your work.
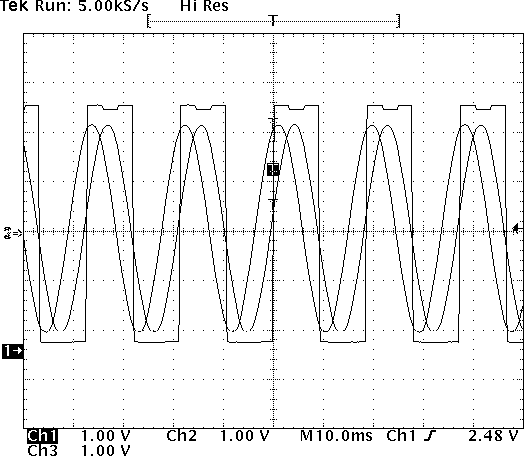
- A snapshot of phasevolt data.
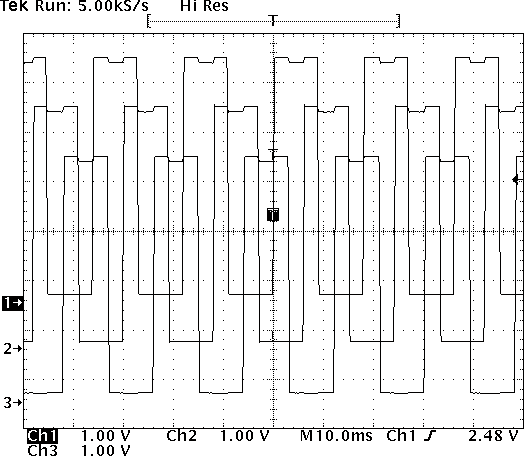
- A snapshot of sensor data.
- When finding a relationship between vag and vhall1, remember that the relationship depends on the value of VDC as given in the MATLAB model. Your answer must account for this. In other words for the relationship vag=f(VDC,vhall1), find the function f.
Post-lab
- The Fourier series of a 2π-periodic function f(x) that is integrable on [-π,π], is given by
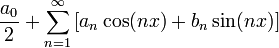
where
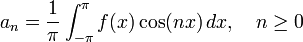
and

- To relate vs to Vdc, you need to find the fundamental component of the Fourier series of the functions vas, vbs and vcs. The fundamental component is the component with the lowest frequency, specifically
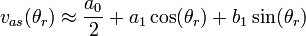
To solve for the coefficients a0, a1 and b1 from the equations above, the integral must be broken down into a sum of integrals over continuous regions.
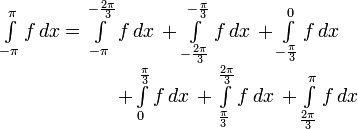
- φv is the angle between Vas and eas. To find this angle, compare zero-crossings near the middle of both curves. If you triggered the oscilloscope on channel 1, then Vas should be crossing zero with a rising edge in the exact middle of the plotted time. eas will cross zero with a rising edge some small time after this point. Measure this difference in time and convert it from seconds to degrees or radians by dividing by the time in one period and multiplying by 360 (for degrees) or 2π (for radians).
Check your work.
- Sample plot of eas, ebs, ecs and hall sensors s1, s2, s3.
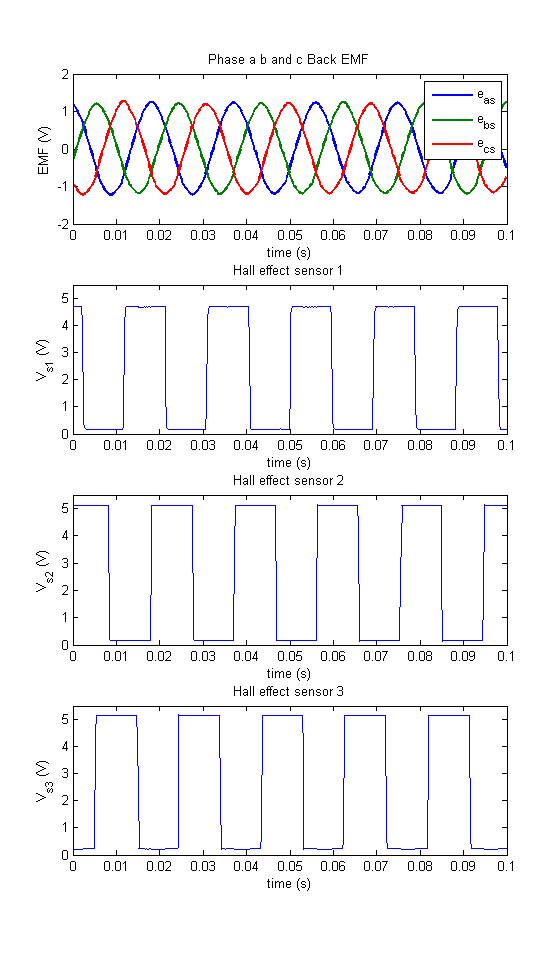
- ωrm ≈ 80 rad/s
- Sample plot of vas, vbs, and vcs.
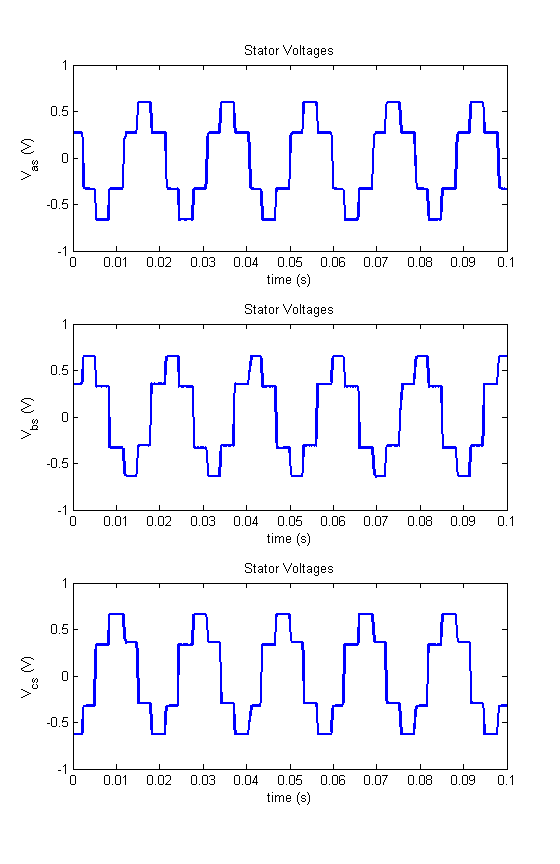
- φv ≈ 25° ≈ 0.4363 rad