Lab 5a Tips: DC Motor
Pre-lab
- Equation (1)-(3) in state space form will look like the system below. The vector u represents inputs to the system (va and TL).
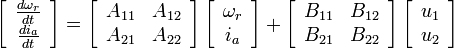
- For steady state use capital letters for variables (capital ω is Ω ).
- Steps for finding the transfer functions.
- Start from equations (1)-(3).
- Neglect LAA.
- Combine equations (1)-(3) to eliminate ia.
- Convert the resulting equation to the frequency domain through application of Laplace transforms using the identities below. Note that the capital form ω is Ω, the symbol we choose for ω in the frequency domain, and that it is safe to assume ωr(0) = 0.
- Linearity:
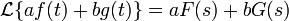
- Differentiation:
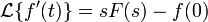
- Solve the resulting equation for Ω (s). Your result should be of the form given below where the parentheses represent constant terms.
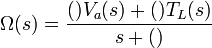
- Solve the above equation for the transfer functions
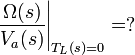
 .
.
- To Find ωr(t), use the first transfer function above and solve for ωr(t) given
va(t) = Vau(t). In other words, solve the following
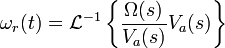 .
.
In-lab
- You can complete the entire lab with this one model.
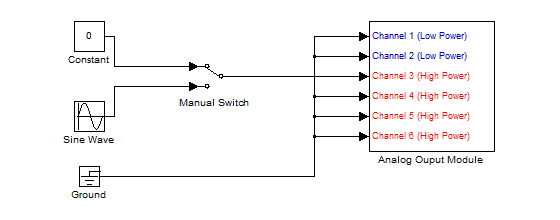
- To convert from torque transducer voltage (as read on ocilliscope) to actual torque use the relations: 1 V = 15 oz-in and 1 N-m = 141.6 oz-in
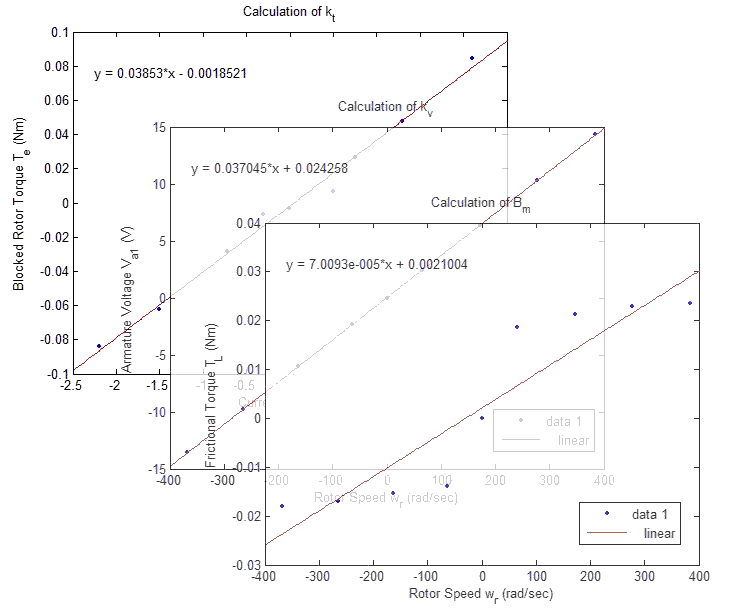
- To find kt, kv, and Bm, use Matlab's built in data fitting features.
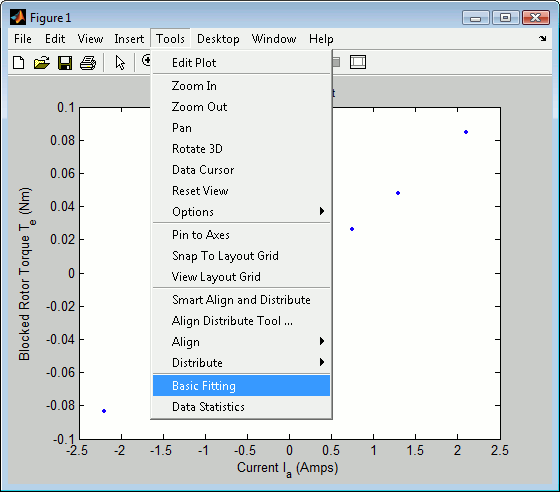
- Select 'linear', 'show equations', and at least three significant digits.
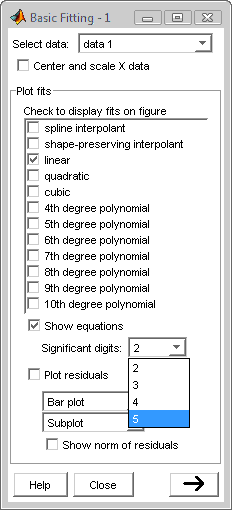
Check your work.
- ra ≈ 2 Ω
- LAA ≈ 4 mH
- kT, kv, and Bm
Post-lab
- For questions 3 and 4, show the relevant equations.
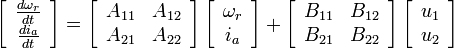
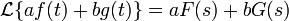
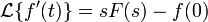
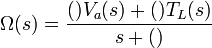
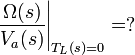
 .
.
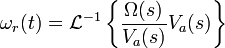 .
.



