Low-Frequency Breakdown

A full-wave solution of Maxwell's equations breaks down at low frequencies, which was observed as early as when the area of Computational EM came into existence. The same breakdown is observed when there exist dense discretizations or fine features relative to working wavelength. This problem is very critical in today's engineering problems analyzed via EM simulators. This is not only because the breakdown frequency of full-wave solvers can fall right within the operating frequencies of an engineering product, but also because there could exist a range of frequencies in which the solution to Maxwell's equations is unknown, since a full-wave solver breaks down while static- and quasi-static solutions are invalid especially in highly multiscaled problems.


The root cause of low-frequency breakdown is finite machine precision, thus the problem is very challenging to solve. We are able to overcome the barrier imposed by the finite machine precision, and successfully find the solution to the original full-wave system of equations from an arbitrarily high electrodynamic frequency all the way down to zero frequency. Our solution is applicable to both PDE- and IE-based methods.


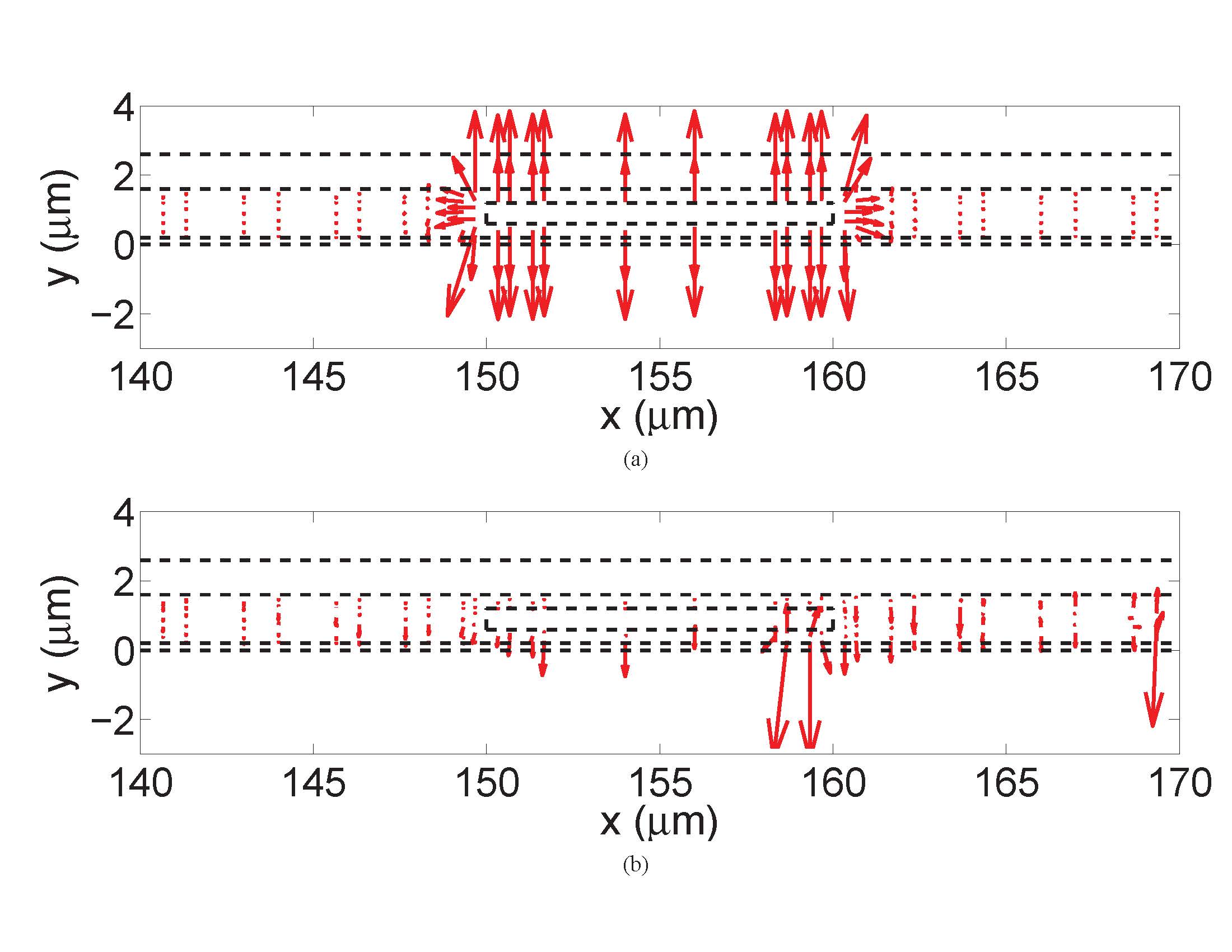
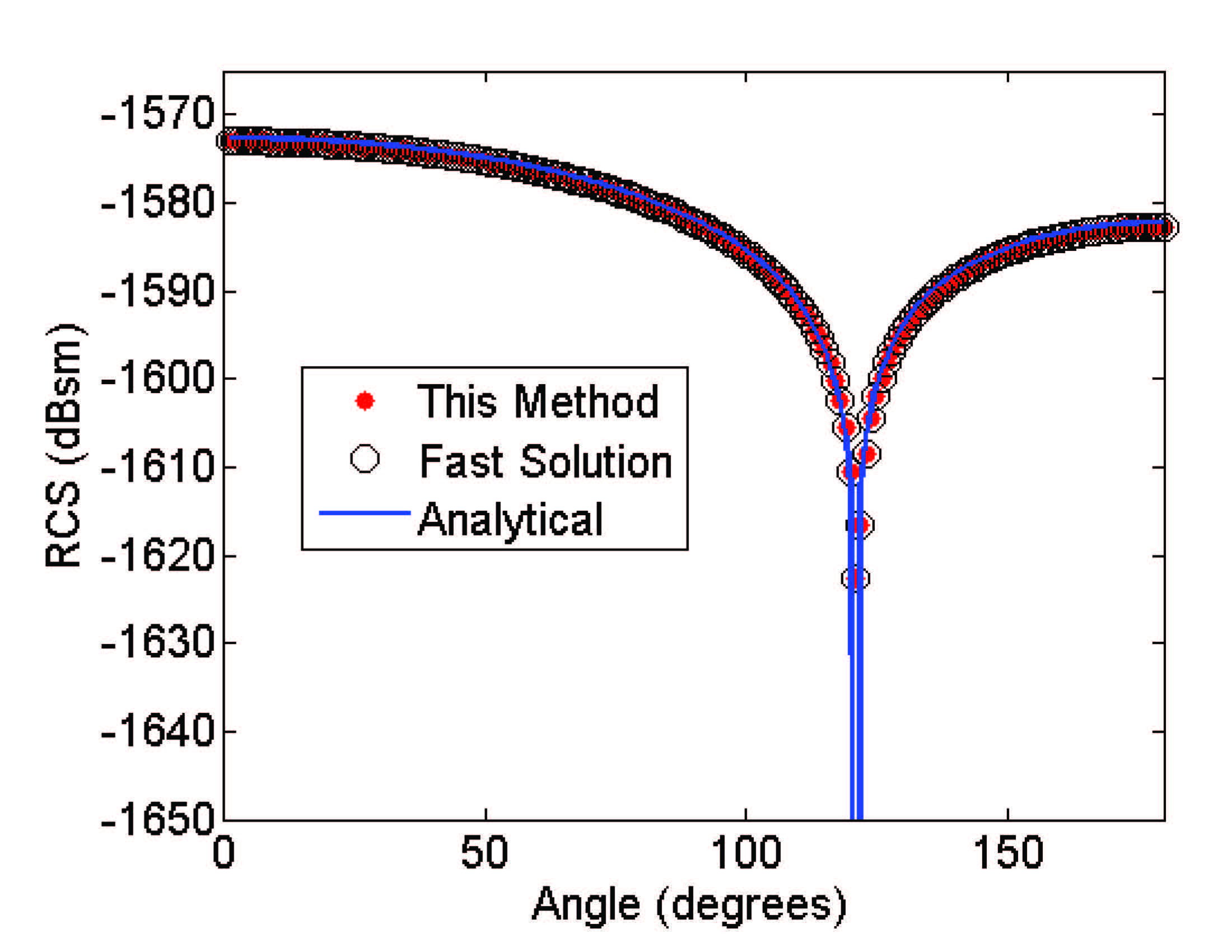
A fast method is also developed to speed up the low-frequency computation in a reduced system of O(1). Moreover, we have demonstrated, both theoretically and numerically, that although the problem is termed low-frequency breakdown, the solution at breakdown frequencies can be a full-wave solution for which static and quasi-static assumptions are invalid for use. This is especially true in multi-scale problems, the geometrical scales of which are many orders of magnitude different. The upper right figure illustrates the RCS of a sphere of 1 m radius at 1e-32 Hz generated by the proposed method in comparison with analytical data. The lower left figure shows the electric field distribution of an on-chip interconnect structure at 1 Hz generated by the proposed method (upper subfigure) in comparison with the field distribution obtained by a conventional method (lower subfigure).

Selected Publications