1. Review of CNotes Chapter. A thoughtful, honest, coherent response to each of the four items below is expected.

A. (2 points) Is the general level of the presentation in Chapter 4 too simple, too difficult, or about right for you?

B. (3 points) Which sections were the most helpful in understanding the material? Which sections were confusing or otherwise inadequate? Which concepts need to be presented better?

2. (10 points) Trip Generation by ITE Method. An manufacturing company is planning to build a 456,000 square foot factory on 55.3 acres in Zone 1 in Middleville. The company plans to employ 975 workers. Use the appropriate ITE information in Figures 4.3 of CNotes Chapter 4 to compute the expected number of trip ends at the factory. (Hint: You should end up with 5 estimates for "T".)

From Figure 4.3a: T= 38.88 x 55.3 = 2150 veh trips per weekday

From Figure 4.3b: T= 3.82 x (456000/1000) = 1742 veh trips per weekday

From Figure 4.3b: T= 38.88 x 55.3 = 1749 veh trips per weekday

From Figure 4.3c: T= 2.10 x 975 = 2048 veh trips per weekday

From Figure 4.3c: T= 1.74 x 975 + 229.975 = 1926 veh trips per weekday

3. Trip Generation by Regression. The Mythaca Regional Planning Commission (MRPC) has not a comprehensive travel survey in many years. For that reason, the staff proposes using the Georgia DOT production and attraction regression equations given below.

P(i) = 93 + (0.1*HH) + (4.0*vehs) + (0.7*empl)

A(i) = 327 + (1.3*HH) + (2.2*empl)

The data for the four Middleville zones are:

Zone 1 has 2475 employees.

Zone 2 has 1073 employees.

Zone 3 has 903 households, 925 vehicles, and a population of 3485.

Zone 4 has 1630 households, 2628 vehicles, and a population of 5228.

A. (12 points) Calculate values of productions and attractions for Zone 1. Use the format shown in Section 1A of the Middleville case study.

B. (3 points) Balance the Ps and As as was done in Section 1B of the Middleville case study.

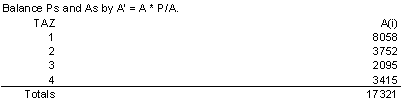
4. (15 points) Trip Distribution. The auto travel times shown in Section 2A of the Middleville case study are still valid, but the MRPC staff wants to use CNotes equation (4.7) to convert those times into Friction Factor values. Use the Gravity Model with a = 1000, b = -2.0, c = -0.75 to complete the other four parts of Section 2A.

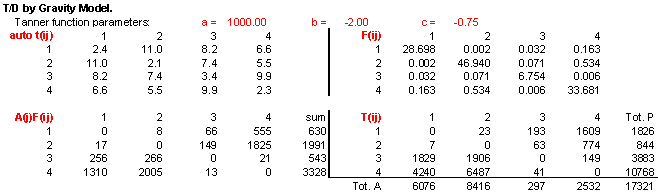
5. (15 points) Mode Choice. The transit travel times shown in Section 3 of the Middleville case study are still valid, but the MRPC staff think they have a better set of parameters to put into CNotes equation (4.8). These parameters are a(0) = 0.76 for auto only and a(1) = -0.36 for both auto and transit. Calculate the transit and auto utilities for each zone pair, then estimate the transit and auto mode shares for each zone pair.

The disutility functions change to:

auto V(m)    = 0.76 - 0.36 x t(i,j)

transit V(m)  = 0.00 - 0.36 x t(i,j)

6. Person-trips and vehicle-trips.

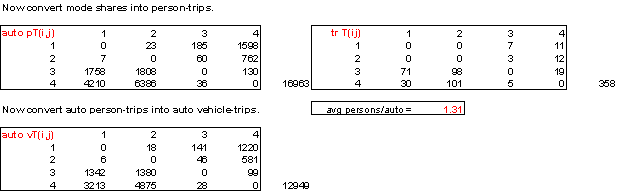
A. (10 points) Convert the auto mode shares found in the previous problem into auto person-trips for each zone pair, as shown in Section 3B of the Middleville case study.

B. (10 points) Using an average vehicle occupancy of 1.31 persons per vehicle, convert the auto person-trips found in Part A into auto vehicle-trips as shown in Section 3C of the Middleville case study.

7. Network Travel Measures.

A. (10 points) Using the interzonal auto travel times and the table of auto vehicle trips, calculate the interzonal auto VHT values as shown in Section 5 of the Middleville case study.

B. (10 points) Using the interzonal auto speeds shown in Section 4 of the Middleville case study, calculate the Interzonal VMT for autos in Middleville.

8. Trip Assignment. An expressway connecting Zones 3 and 1 has an LPF t(X) = 8.0 + 5.7 V(X), where V(X) is in 1000s of vehicles per hour in a given direction. The old arterial streets between Zones 3 and 1 are still available, with an LPF of t(A) = 9.9 + 13.5 V(A).

A. (10 points) If all drivers from Zone 3 to Zone 1 want to minimize their individual travel times, at what flow rate V(X) will drivers begin to divert back to the arterial route?

If drivers from Zone 3 to 1 want to minimize their individual travel times, the individual travel time in the expressway has to increase to the travel time in the arterial with no vehicles on it.

LPF t(X) = 8.0 + 5.7 V(X) = 9.9 + 13.5 V(A) where V(A) = 0.0

8.0 + 5.7 V(X)  = 9.9

5.7 V(X) = 1.9

V(X) = 1.9/5.7 = 0.333 ... 333 vehicles

B. (10 points) If T(3,1) = 2663 vph during the peak hour, find the equilbrium travel time from Zone 3 to Zone 1 and calculate V(X) and V(A) for the peak hour.

8.0 + 5.7 V(X) = 9.9 + 13.5 V(A) 

V(X) + V(A) = 2663 vph

V(X) = 2.663 - V(A)

8.0 + 5.7 (2.663 - V(A)) = 9.9 + 13.5 V(A)

8.0 + 15.179 - 5.7 V(A) = 9.9 + 13.5 V(A)

13.279 = 19.2 V(A)

V(A) = 0.6916 ... 692 vehicles

V(X) = 2663 - 692 = 1971 vehicles

Equilibrium travel time

LPF t(X) = 8.0 +   5.7 V(X) = 8.0 + 13.5 x 1971 = 19.237 time units

LPF t(A) = 9.9 + 13.5 V(A) = 8.0 + 13.5 x  692 = 19.237 time units