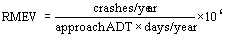
Dear Consultant:

The stretch of SR835 in HW5 that was thought to be dangerous will be analyzed further in this HW. Please demonstrate the use of proper methods and present your work clearly and concisely.

Note: As in previous HWs, you may submit this HW as a member of a group formed by the mutual consent of no more than four CE361 students. If this HW is submitted by a group, the top sheet of the material submitted must bear the signature of each group member. Each member of a group that submits HW6 in this way will receive the same grade.

1. Review of Course Notes Chapter 6 (Safety on the Highway). Again, a useful response to each of the items below is encouraged.
A. (2 points) Is the general level of the presentation in Chapter 6 too simple, too difficult, or about right for you?
B. (3 points) Which sections were the most helpful in understanding the material? Which sections were confusing or otherwise inadequate? Which concepts need to be presented better?

2. Crash rates.
A. (10 points) Using the Web or other source, determine the number of motor vehicle crashes that occurred in the US during a recent year. For the same year, how many vehicle miles were driven in the US? (Cite the sources of the two numbers you use.) From these two numbers, calculate an overall national crash rate.

1998 - Vehicle Crashes 6,335,000 website: http://www.nhtsa.dot.gov/people/ncsa/tsf-1998.pdf

1998 - Vehicle Miles Traveled 2,618,701x10⁶ website: http://www.nhtsa.dot.gov/people/ncsa/tsf-1998.pdf

National Rate = 6,335,000/2,618,701 = 2.42 crashes per million VMT = 242 crashes per hundred million VMT

B. (10 points) A 9.15-mile section of SR835 had six crashes recorded in 1997, 12 in 1998, and 8 in 1999. The most recent traffic count was 7025 veh/day. What is the crash rate for that section? Is it appropriate to compare the SR835 crash rate with the national rate computed in Part A? Why (not)?

9.15-mile length section

1997 - 06 

1998 - 12 

1999 - 08 

Average number of crashes = 8.67

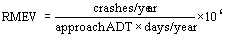
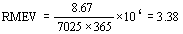(per million) = 338 crashes per hundred million entering vehicles

VMT = 9.15 x 7025 x 365 = 23,461,743.75 VMT

Rate = 8.67 / 23.461 = 0.37 crashes per million VMT = 36.955 per hundred million VMT

This rate can be compared to the national rate, which is higher than the road segment at SR835.

C. (10 points) Regardless of your answer to Part B, assume the crash rate was 31.2. Seven other "similar" stretches of highway in Mythaca's part of the state had crash rates of 18.1, 22.3, 22.4, 18.1, 37.9, 34.9, and 28.9. Using the Critical Rate Analysis, determine whether SR835 is a hazardous road.

Rate = 31.2 crashes per million VMT

Critical Rate Analysis

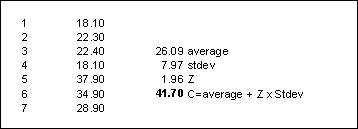
Because 31.2 is lower than 41.70, we can say that this road segment is not hazardous.

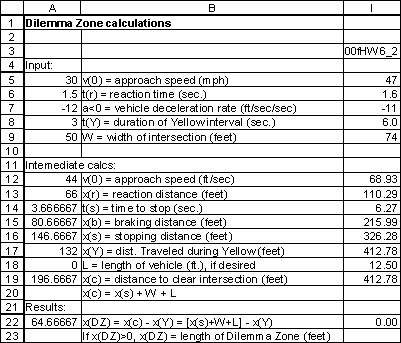
3. (15 points) Dilemma Zone. The section of SR835 under study ends at an intersection with US23. The 85th percentile approach speed is 47 mph. Using a driver reaction time of 1.6 seconds, a vehicle deceleration rate of 11 ft/sec/sec, and a vehicle length of 12.5 feet, determine the minimum length of the yellow signal phase needed to prevent a dilemma zone. The intersection is 74 feet wide.

v(o) = 47 mph

t(r) = 1.6 sec

a<0 = -11 ft/sec/sec

L = 12.5 ft

W = 74 ft

v(o) = 47*(5280/3600) = 68.93 ft/sec

x(r) = 1.6*68.93 = 110.29 ft

t(s) = 68.93/-(-11) = 6.27 sec

x(b) = 68.93*6.27 + -11*0.5*6.27² = 215.99 ft

x(s) = 110.29 + 215.99 = 326.28 ft

x(Y) = Y * 68.93

x(c) = 12.5+74+326.28 = 412.78 ft

What you need to do is to change the length of the yellow signal length in order to make x(DZ)=0

x(DZ) = x(c) - x(Y) = [x(s)+W+L] - x(Y)

Using solver or goal seek tools in Excel, you can do this.

The result is 6 seconds.

4. (15 points) Sight distance on a hill. At one point on SR835, there is an uphill grade of 2.7 percent, a crest vertical curve, then a 4.9 percent downhill grade. The length of the curve is 676 feet. What design speed will ensure an adequate design stopping sight distance?

L = 676 ft

A= abs (2.7- (-4.9)) = 7.6

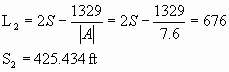
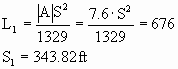
Because the calculated SSD is less than the length of the curve, the second equation should be used, so SSD=343.82 ft.

Using Table 6.8, the answer is between 40 mph (SSD=325) and 45 mph (SSD=400), choose 40 mph.

5. Transition curves.
A. (10 points) Spiral curves. Two circular curves on SR835 are connected by a spiral curve that is 587 feet long. The radii of the two circular curves are 900 feet and 1300 feet. What is the maximum safe speed on the spiral?

L = 587 ft

R1 = 900 ft

R2 = 1300 ft

V = 69.11 mph (remember the units for Ls and Rmin are feet, and for V mph in this equation)

B. (10 points) The circular curve with a radius of 900 feet needs to be super elevated. Assuming a design speed of 55 mph, what should be the super elevation rate e (taken from Table 6.9) that should used in the curve? The lanes are 12 feet wide. How much super elevation runoff length is needed for this banked curve?

L = 900 ft

Assuming a maximum value of e of 0.04, and from Table 6.9 you can get a Maximum radius of 1,186 ft, which is higher than 900 ft.

Now, using Table 6.10, and for a speed of 55 mph with an e of 0.04, you can get a runoff of 152.5 ft. However, this values lies in the shaded area which is not permitted. The value used has to be under the darker line. Therefore, using a value of e of 0.08 and a runoff of 202.5 ft is the appropriate thing to do.

6. (15 points) Stopping Sight Distance for Horizontal Curves. A tight (R = 75 feet) horizontal curve takes vehicles around a warehouse that is 31 feet from the edge of the roadway. Each of the street's two lanes are 10 feet wide. What should be the speed limit (operating speed) for this curve?

R=75 ft

Rv = 75 - 10/2 = 70 ft

Ms = 31 + 10/2 = 36 ft

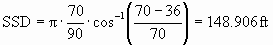
Using Table 6.8 shows that for a SSD= 150 ft, the speed limit should be 25 mph.