Purdue University School of Civil Engineering Faculty of Geotechnical Engineering Engineering Geology - Underground Construction - Rock Mechanics

Numerical Modeling with FROCK

• Description of FROCK
• Criterion for crack initiation
• Comparison of numerical and experimental results
• Conclusions

1. Description of FROCK

FROCK is a Displacement Discontinuity Method (DDM) in which the boundaries of the continuum are discretized into small elements. The advantages of the DDM are that it only requires discretization at the boundaries of the continuum and that, unlike the Finite Element Method (FEM), it does not need re-discretization for any new crack.

The code was initially written by Chan (1991) in FORTRAN but has now been rewritten in C. The following fundamental improvements have been made: portability between different computer platforms, graphical output during and after execution, capability of handling open and closed flaws, and a new crack initiation and propagation criterion.

The graphical output capabilities are written in the X11 code, and consist of an internal module for the display of the cracks generated in real time execution and of an independent program, used as a post-processor, for later analysis of the results.

The code has been extensively checked by comparing its results with closed-form solutions and with the FEM ABAQUS. Also, the stresses around the tips of flaws as obtained from closed-form solutions have been compared with the results from FROCK. All these comparisons and verifications result in a very good agreement between the three methods: closed-form solution, FEM and FROCK.

The next figure shows the comparison of KII obtained from theory, FROCK and ABAQUS. An isolated flaw with a total length of 12.7 mm, in an infinite medium with an inclination angle of 45° with respect to the load, is used for the numerical tests. The flaw is considered closed with the following properties: coefficient of friction= 0.283, and cohesion= 8.66 MPa. Observe from the figure that KII is zero until the external stress reaches a critical magnitude; the critical stress is such that the shearing resistance in the plane of the flaw is overcome. At this point the flaw debonds and loses its cohesion; it can be seen from the figure that the stress intensity factor increases instantly.

2. Criterion for crack initiation

The new criterion is formulated as (see next figure):

• Tensile and shear cracks initiate from the tips of the flaws.
• There exists a region around the tip of the crack in which the material has yielded. As a first approximation the shape of the plastic region is taken as cylindrical, with the center at the tip of the flaw, and with dimensions defined by the radius ro, which depends on the material and on the loading mode (see detail (a)).
• A tensile crack will initiate in the direction perpendicular to the maximum tensile tangential stress, and when this stress reaches a critical value which is material dependent (see details (b) and (c)).
• A shear crack will initiate in a direction in which the absolute value of the shear stress attains a maximum. It will propagate when the maximum shear stress reaches a critical value which is also material dependent (see details (b) and (c)).

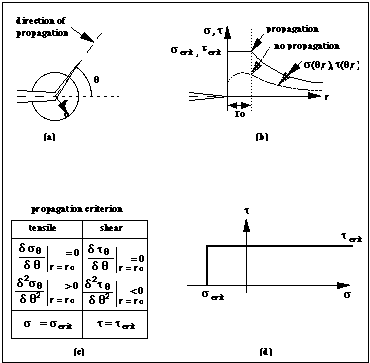Thus, the initiation criterion requires three parameters: the critical tensile strength of the material, the critical shear strength of the material and the core radius ro. The critical strengths are assumed to be material properties, and the core radius changes with the loading mode (uniaxial, biaxial compression, tension) as well as with the material.

3. Comparison of numerical and experimental results

The values of the three material parameters can be obtained with only one test per loading mode, since for each test at least three measurements can be taken: wing crack initiation stress, wing crack initiation angle, and coalescence stress (if coalescence occurs).

Once the parameters are determined, the propagation criterion is validated by comparison of the experimental results obtained from uniaxial and biaxial compression tests, with the predictions obtained with the model. Wing crack initiation stresses and angles, coalescence stresses, crack types and coalescence patterns can be satisfactorily predicted by FROCK, for open and closed flaws and for uniaxial and biaxial compression. Predictions and experimental results lie mainly within the experimental error.

The figure below shows a comparison between the crack pattern predictions and the experiments for coalescence type II. The following observations from experiments are also captured by the model:

(1) Two types of cracks are obtained: tensile and shear cracks (2) The cracks initiate from the tips of the flaws and propagate in a stable manner. (3) The internal and external cracks initiate at the same time. (4) The wing cracks initiate at the same time as the shear cracks. (5) Shear cracks initiate in a plane which is coplanar or roughly-coplanar with the flaw. (6) Coalescence is produced through an unstable propagation of one or both of the internal cracks. (7) The model can even predict that in coalescence type II (see next figure), the internal shear cracks propagate and link in an unstable manner through a tensile crack in the middle of the ligament.

Results of experiments performed by other researchers in the same material such as Reyes and Einstein (1991) and Shen et al. (1995) but for different geometries in uniaxial compression are also in good agreement with predictions from FROCK.

Very importantly, experimental results obtained in tension can also be predicted by the model. Takeuchi (1991) diametrically loaded pre-cracked specimens of gypsum (Brazilian tests) and observed the stresses and angles of crack initiation. Again the agreement between predictions and experimental results is very good.

4. Conclusions

The assumptions relative to the yield surface and to the crack initiation are very simple. Even though more complicated yield surfaces and plastic regions could be implemented, their introduction in the model is not warranted from the experimental evidence available so far. Over one hundred experiments, including open and closed flaws, different flaw geometries and loading modes have been compared with the numerical model. In that sense the propagation criterion has been sufficiently validated. Nevertheless this model has its limitations. The model is still in its conceptual stages of development, although its predictions are remarkably good.

References

Chan, H.C.M., V. Li, and H.H. Einstein (1990). A hybridized displacement discontinuity and indirect boundary element method to model fracture propagation. International Journal of fracture , 45, 263-282.

Reyes, O. and H.H. Einstein. Failure Mechanism of Fractured Rock- A Fracture Coalescence Model. Proceedings 7th International Congress of Rock Mechanics, Vol. 1, 333-340, 1991.

Shen, B., O. Stephansson, H.H. Einstein, and B. Ghahreman. Coalescence of Fractures under Shear Stress Experiments. Journal of Geophysical Research, 100, 5975-5990, 1995.

Takeuchi, K. Mixed-Mode Fracture Initiation in Granular Brittle Materials. M.S. Thesis, Massachusetts Institute of Technology, Cambridge, U.S.A., 1991.

Page Up Resume Teaching Research Home