|
|||
|
Current distribution calculations Antenna design and simulations RCS & Bi-RCS computations Current distributions on metallic plates Inverse scattering simulations Experimental inverse scattering
|
Monostatic and Bistatic RCS Computations: Hybrid Finite-Element Boundary-Integral Method for 3D Scattering
The main idea of this hybrid method is to use a Finite-Element formulation in the
interior region of the discretized scattering object and a Boundary-Integral Equation
formulation in the exterior region. For more information about this technique, please
refer to Prof. Jianming Jin's book, ``The Finite Element Method in Electromagnetics
'', whose description can be found
here.
In the following, numerical simulation results will be shown. The problems are solved using the Multi-Level Fast Multipole Algorithm (MLFMA), and matrix inversions are using a Conjugate Gradient (CG) method. If you want to know more about the MLFMA, check this page.
The first Figure shows the test object, a coated sphere. The second one shows
the normalized residual norm versus the number of iterations
in the CG solution of scattering by a coated sphere, for both interior resonant and
non-resonant cases. Then, the two following Figures show
the bistatic RCS of the coated sphere, for both resonant and
non-resonant cases. Good results are obtained using the new
hybrid formulation (labeled TENENH).
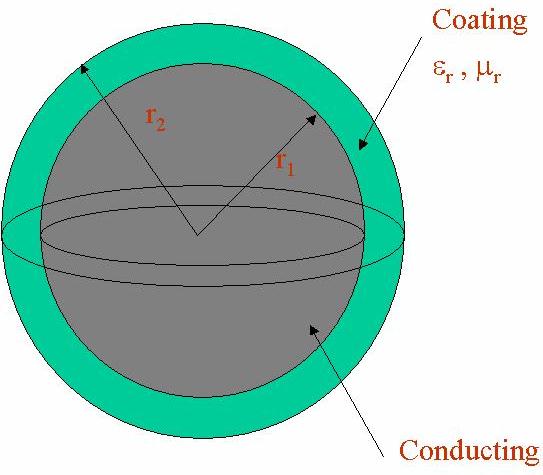 Coated sphere  Normalized residual norm, non resonant case 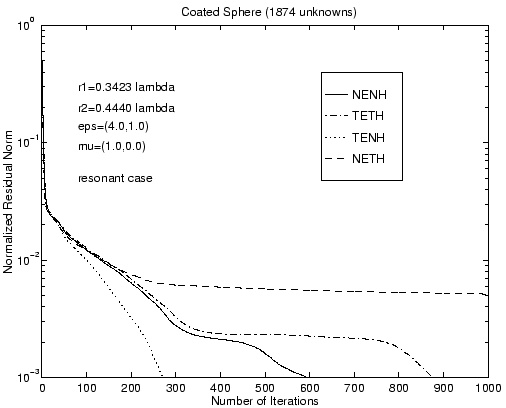 Normalized residual norm, resonant case 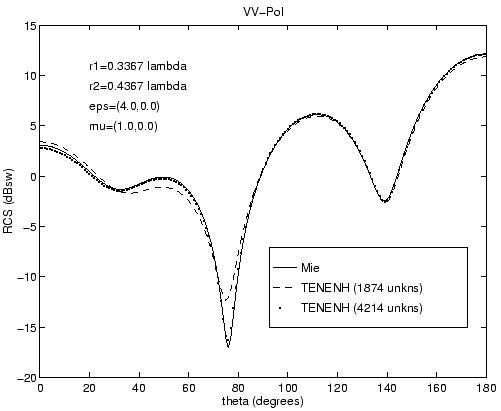 Bistatic RCS of the coated sphere, non resonant case  Bistatic RCS of the coated sphere, resonant case
The following two Figures compare the accuracy of the computed RCS with the
analytical Mie-series solution as a function of the number of levels in
the Fast Mulipolt Method.
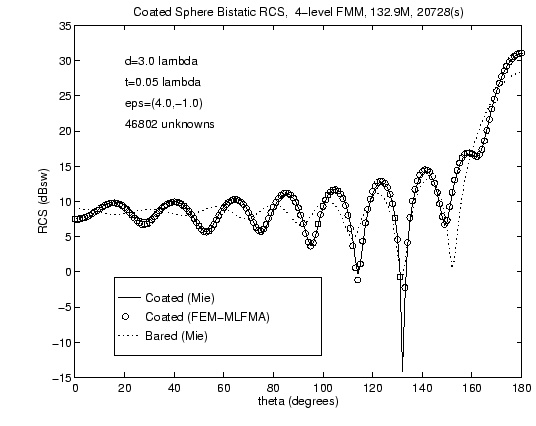 RCS of the coated sphere with a 4-level FMM  RCS of the coated sphere with a 5-level FMM
The final two Figures show the computation of the monostatic RCS of two
real objects: a Northrop wing and a NASA almond. More information about these
results are self-contained in the Figures.
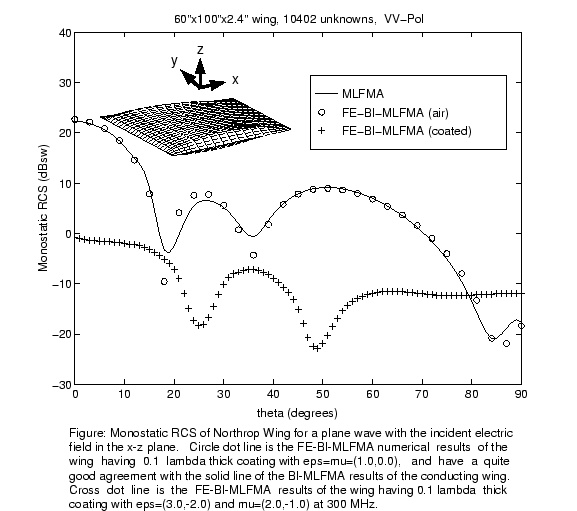 RCS of the Northrop wing  RCS of the NASA almond The above work is a collaboration between X.Q. Sheng, Dr. JinMing Song, Dr. Caicheng Lu, Prof. Jianming Jin, and Prof. Weng Cho Chew. Please send suggestions, comments, and inquiries to: song@sunchew.eceuiuc.edu.
|