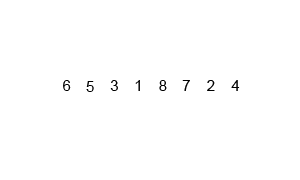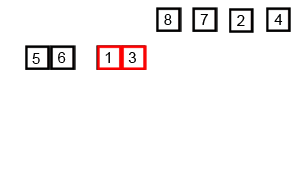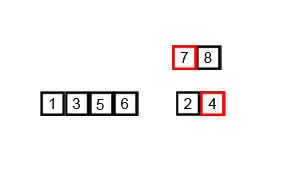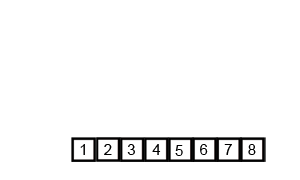Sorting
Goals
- Practice writing code using linked lists and binary search trees (dynamic structures).
- Practice writing code using recursion.
- Learn to use function addresses
(function pointers). - Learn to use the
qsort(…)function. - Gain some perspective on different sorting algorithms.
Overview
In this assignment, you will implement the merge sort algorithm for linked lists.
To add some perspective, you will also implement a tree sort (based on
binary search trees) and write a wrapper function for the standard
qsort(…) function, an implementation of the
quicksort algorithm. However, the main focus on merge sort and linked lists.
There are no starter files.
About Merge Sort
Recursion is an elegant method for solving many problems. At first it can seem unnatural; however, it is actually very simple once you are used to it. The key thing to understand is that recursive programming has two steps:
- A base case which is trivial.
- A recursive case where you write the solution for the larger case in terms of the solution to smaller cases.
What makes (2) easy is that you simply assume that you have the solution of a smaller case. Life does not generally let you assume you have a solution that you have not yet found; however, if you think about it, it should be obvious (by induction) that recursion works this way.
In this assignment, we will use (1) and (2) above to sort linked-lists of integers using the "merge-sort" algorithm. Merge-sort is a beautiful algorithm that sorts extremely quickly with large inputs. It is also the best possible algorithm to use for sorting linked-lists.
Merge sort works as follows:
-
Base case:
You never need to sort a list of length 0 or 1; it is already "sorted", so-to-speak. To implement the base case, simply return the input list if its length is 0 or 1. (In general, base cases are trivial like this.) -
Recursive case:
Lets wave our hand, and assume that we know how to sort smaller lists already. (See, recursion is easy.) For the recursive case, we do the following:- Divide the list into two smaller lists of equal size, +/- one node.
- Recursively sort each of the two smaller lists. (Wow: easy.)
-
You now have two small lists that are sorted. To produce the final large
sorted list, you "merge" the two smaller lists together.
- Create a brand new empty list, which will be the result-list.
- While both small lists are non-empty, look at the head node of each. Take the smaller head node off of the front of its list, and append it to the result-list.
- Eventually one (or perhaps both) of the smaller lists will be empty. At this stage, append the non-empty list (if there is one) onto the end of the result-list.
// Credit: Aaron Michaux, Prof. Yung-Hsiang Lu … This description adapted from a previous ECE 264 assignment
TDD steps
Do the assignment in the following order:
- BST, size==0 (empty)
-
Add a test for
create_bst(…)andempty_bst(…)assuming an empty array (i.e.,array == NULLandsize == 0) -
Implement just enough of
create_bst(…)andempty_bst(…)to pass the test you just wrote. -
Hint: Body of your
create_bst(…)can—and probably should—be exactly one sloc, assuming you use a compound literal. Body of yourempty_bst(…)should be empty. -
At this point, there should be
no calls to
malloc(…)orfree(…)anywhere. - Test. (Debug, as needed.)
- Submit
-
Add a test for
-
BST, size==1
-
Add a test for
create_bst(…)andempty_bst(…)assuming an array of size==1. -
Implement just enough of
create_bst(…)andempty_bst(…)to pass the two tests you have written so far. -
⚠ Do not implement any more than is required to pass your two tests.
If your sorts.c contains
any recursive calls,
any
else if, or any conditions that compare the value in the root to a value from the array, you are not following directions and should expect a penalty. -
Body of your
create_bst(…)may comprise as few as 6 sloc. No helper functions are necessary at this point. (It is fine if you have a helper function, as long as you are not implementing any more logic than necessary to pass this test.) -
Body of your
empty_bst(…)should be exactly 3 lines (using) a compound literal. Your sorts.c should contain exactly one call tomalloc(…)and one call tofree(…). - Test. You should be passing both tests now. Debug and retest, as needed.
- Submit
-
Add a test for
-
BST, size ≥ 2
-
Add a test for
create_bst(…)andempty_bst(…)assuming an array of any size. -
Implement just enough of
create_bst(…)andempty_bst(…)to pass the tests you have written so far. Follow the patterns demonstrated in class. -
Reminder #1: Helper functions should be named beginning with
'_'. -
Reminder #2: Helper functions must be declared as static
(ex:
static void _insert(…) { … }). - Your code can—and should—be very similar to the code from lecture, but you are expected to write it yourself from scratch. Take a few minutes to study it. Jot down a few notes in English (or your preferred human language), if you like. Then, close the window and write the code on your own.
- Test. You should be passing all tests. Debug and retest, as needed.
- Submit
-
Add a test for
-
tree_sort_array(…), size ∈ {0,1}-
Add a test for
create_bst(…)andempty_bst(…)assuming an array of any size. -
Implement just enough of
tree_sort_array(…)to pass your new test (without breaking any others). -
This step should require no changes to your
create_bst(…)orempty_bst(…). -
⚠ Do not implement any more than is required to pass your two tests.
Your
tree_sort_array(…)should be extremely short—i.e., as short as a function can be. (Get my drift?) - Test (all). Debug.
- Submit
-
Add a test for
-
tree_sort_array(…), any size-
Add at least one test for
tree_sort_array(…)for sorting arrays of any size. -
Finish implementing
tree_sort_array(…). - Hint: You already know how to print the values in a BST using an in-order traversal. What if instead of printing each value to the screen, you outputed it to somewhere else… perhaps an array?
- Test (all). Debug.
- Submit
-
Add at least one test for
-
create_list(…)andempty_list(…)-
Add at least one test for
create_list(…). Be sure to test creating/emptying lists of size=0, size=1, and size≥2. -
Implement just enough of
tree_sort_array(…)to pass your new test (without breaking any others). -
This step should require no changes to
create_bst(…),empty_bst(…),tree_sort_array(…). -
⚠ Do not implement any more than is required to pass your two tests.
Your
tree_sort_array(…)should be extremely short—i.e., as short as a function can be. (Get my drift?) - Test. (Debug, as needed.)
- Submit
-
Add at least one test for
-
merge_sort_list(…)for size ∈ {0, 1}, and other arrays that are already sorted-
Add at least one test for
merge_sort_array(…)for arrays of size ∈ {0, 1}, as well as arrays of any size that are already sorted. -
Implement just enough of
merge_sort_list(…)merge_sort_array(…)to pass this test.-
Hint:
merge_sort_list(…)andmerge_sort_array(…)will both be extremely short… like as short as any function can be.
-
Hint:
- Test (all). Debug.
- Submit
-
Add at least one test for
-
merge_sort_list(…)for any list-
Add at least one test for
merge_sort_list(…)on lists of size ≥ 2 that are not yet unsorted. -
Finish
merge_sort_list(…). - Test (all). Debug.
- Submit
-
Add at least one test for
-
merge_sort_array(…)for any list-
Add at least one test for
merge_sort_array(…)on arrays of size ≥ 2 that are not yet unsorted. -
Finish
merge_sort_array(…). This is just a wrapper formerge_sort_list(…). You must copy the array elements to a new linked list usingcreate_list(…), sort the list usingmerge_sort_list(…), and then copy the sorted values back from the list into the array.⚠ Do not attempt to sort the array in any other way. - Test (all). Debug.
- Submit
-
Add at least one test for
-
quick_sort_array(…), any size array-
Add at least one test for
quick_sort_array(…). -
Implement
quick_sort_array(…). - Test (all). Debug.
- Submit
-
Add at least one test for
-
Add enough tests and/or additional implementation code to be confident that your
submission meets the requirements (↓) and has no bugs.
- ⚠ Double-check that filenames are named correctly.
- ⚠ Double-check that functions have the correct signature (return type and parameters).
- Submit
Requirements
- Your submission must contain each of the following files, as specified:
- Whenever
size==0,headandtailmust be NULL. - Whenever
size==0,rootmust be NULL. - Do not include helpers (if any) here.
- Do not merge sort the array directly. This must use your
merge_sort_list(…). - Store the result in the same array that was passed in.
-
Steps: ① call
create_list(…), ② callmerge_sort_list(…), ③ store the sorted values inarray(same memory), ④ callempty_list(…). - The purpose is to make
merge_sort_list(…)comparable with the other sort functions. - This may not result in any heap allocation (i.e., calls to
malloc(…)), except for the list nodes allocated as a result of callingcreate_list(…); those must be freed before this function returns. -
Steps:
① call
create_bst(…), ② use in-order traversal to store sorted values inarray(same memory), ③ callempty_bst(…). - Store the result in the same array that was passed in.
- This may not result in any heap allocation (i.e., calls to
malloc(…)), except for the BST nodes allocated as a result of callingcreate_bst(…); those must be freed before this function returns. - This should simply call the
qsort(…)library function. - The
qsort(…)function requires the use of function addresses (function pointers). - This may not result in any heap allocation (i.e., calls to
malloc(…)) by your code. - Yes, this is easy, but make sure you understand how it works!
sizeis the number of elements inarray.- When size==0 array must be NULL and vice versa.
- If size==0 then return a list with the head and tail set to NULL.
malloc(…)may be called from a total of one place in this function and any it depends on.- This may not result in any heap allocation (i.e., calls to
malloc(…)). - Set
headandtailto NULL, andsizeto 0. free(…)may be called from a total of one place in this function and any it depends on.sizeis the number of elements inarray.- When size==0 array must be NULL and vice versa.
- If size==0 then return a BST with the root set to NULL.
malloc(…)may be called from a total of one place in this function and any it depends on.- Set
rootto NULL, andsizeto 0. free(…)may be called from a total of one place in this function and any it depends on.- This must cause every line of code in your sorts.c to be executed.
- Every public function in sorts.c must be called directly from
main(…)and/or from a helper within test_sorts.c. - Use the
typedefsyntax to declare all struct types. - Only the following externally defined functions and constants are allowed in your .c files. (You may put the corresponding #include <…> statements in the .c file or in your sorts.h, at your option.)
Feel free to suggest additional header files or functions that you would like to use.header functions/symbols allowed in… stdbool.h bool,true,falsesorts.c,sorts.h,test_sorts.cstdio.h printf,fprintf,stdout,FILEtest_sorts.cstdlib.h malloc,free,NULL,EXIT_SUCCESS,EXIT_FAILUREsorts.c,test_sorts.c,sorts.hassert.h assertsorts.c,test_sorts.c - Submissions must meet the code quality standards and the policies on homework and academic integrity.
| file | contents | |
|---|---|---|
| sorts.h | type definitions |
List
struct type with 3 fields: head (ListNode*), tail (ListNode*) and size (int)
|
|
ListNode
struct type with 2 fields: value(int), next (ListNode*)
|
||
|
BST
struct type with 2 fields: root (BSTNode*) and size (int).
|
||
|
BSTNode
struct type with 3 fields: value(int), left, and right (BSTNode*)
|
function declarations |
one for each required function in your sorts.c
|
| sorts.c | function definitions |
merge sort array(int✶ array, size t size)
→ return type: void
Sort array using merge_sort_list(…).
|
tree sort array(int✶ array, size t size)
→ return type: void
Sort array by creating a BST and then traversing it.
|
||
quick sort array(int✶ array, size t size)
→ return type: void
Sort array using the qsort(…) standard library function.
|
||
create list(const int✶ array, int size)
→ return type: List
Create a new List.
|
||
merge sort list(List✶ a list)
→ return type: void
Merge sort list.
|
||
empty list(List✶ a list)
→ return type: void
Free all the nodes in the list.
|
||
create bst(const int✶ array, int size)
→ return type: BST
Create a new BST.
|
||
empty bst(BST✶ bst)
→ return type: void
Free all the nodes in the BST.
|
||
| test_sorts.c | function definitions |
main(int argc, char✶ argv[])
→ return type: int
Test your functions in sorts.c.
|
| expected.txt | functions | Expected output from running your test_sorts.c |
Submit
To submit HW15 from within your hw15 directory,
type
264submit HW15 sorts.h sorts.c test_sorts.c expected.txt
Pre-tester ●
The pre-tester for HW15 has been released and is ready to use.
Q&A
-
Where's the starter code? How am I supposed to start?
Learning to program in C entails learning to set up your files and code your project to meet a specification—without being given step-by-step instructions. That said, here is a general process you can use for doing that.How to do any coding homework in ECE 264- First, identify the files you are responsible for producing. In this case, there are four files: sorts.c, sorts.h, test_sorts.c, and expected.txt. Create an (almost) empty file for each.
-
In the .c and .h files, add a Vim modeline. (Tip: In Vim on ecegrid, type
newcand press Tab to get a skeleton file, including the modeline. Remove any#includestatements or anything else that isn't needed or allowed.) - In the .h file (sorts.h), add an include guard.
- Create your makefile. This is optional, but recommended. You do not need to use miniunit.h or clog.c in order to use make (but you may if you wish).
- Submit. Your code is nearly empty, but this gives you a backup.
make submit(or264submit sorts.h sorts.c test_sorts.c expected.txtfor Luddites). -
Decide on a general order in which to implement the various parts of
the assignment. For HW15, you could do the
three parts in any order. If you have no opinion, we lightly suggest
doing in this order:
①
merge_sort_array(…), ②tree_sort_array(…), ③quick_sort_array(…). But again, it's up to you. - In your test code file (test_sorts.c), create your first test.
- Write one very simple test (e.g., sort empty array). At this point, your sorts.c should have no useful code in it.
- Write just enough code in sorts.c to pass your easy test.
-
Run your test (e.g.,
make test(or./test_sortsfor Luddites). Hopefully, your simple test passes. This step is to test the mechanics of your testing, and verify that you have the correct function signatures and such. - Add a slightly harder test (e.g., sort array of size one).
- Add code to your sorts.c so that both of your tests should pass.
- Run your tests. Make any fixes so that both of your tests do pass.
-
Gradually add tests, extend implementation, run tests, and fix, until one
section of your project is complete (e.g., until
merge_sort_array(…)is working). - Follow the above steps to complete the rest of HW15.
- Re-read the specification—especially the Requirements table—and make sure you have done everything, and your types/fields/functions all match the specification.
-
Check for gaps in your tests. Make sure you get 100% line coverage from
make coverage. This is no guarantee of perfection, but if you don't have 100% coverage, you need to fix that. Make sure your tests cause every part of your implementation code to be executed. -
Think through your tests carefully. Make sure you have covered all:
- “edge cases” – extreme values
- “corner cases” – values that cause your code to behave differently
- “special cases” – exceptions to normal functionality described in the specification
- "easy cases" – easy for you to understand
-
Can I add helper functions to sorts.c?
Yes. Make sure the names begin with "_". -
Is there a warm-up?
No. -
Is it a violation of the spec if
qsort(…)callsmalloc(…)?
No. The only requirement is that your code not callmalloc(…)as a result of callingquick_sort_array(…). -
Should I use recursion for the BST operations
(
create_bst(…),tree_sort_array(…), andempty_bst(…))?
Short answer: Yes.Long answer: All of these things can be accomplished without recursion, using onlywhileloops. However, those methods are messier.The methods demonstrated in class (see snippets) use recursion, and that is what we recommend. -
How do I create a BST? … delete a BST?
To create a BST, start with an empty BST (root = NULL) and then insert each element you wish to add.To delete a BST, delete the left and right subtree (recursively). Then, free the root.The bst.c snippet from 2/21/2019 illustrates everything you need to do. You may not copy that snippet, but once you understand it, you should have no trouble doing what you need to do with BSTs for HW15. -
What is “in-order traversal”?
That is just a fancy name for the method of printing a BST shown in the snippet from 2/21/2019.With in-order traversal means you “visit” (i.e., do something with) the left subtree, then the root, and finally the right subtree. In that example, “visit” meant printing the value of a node. For a BST, this results in printing the values in order.You will learn a bit more about tree traversals later, but for HW15, this is all you need to know.Example:In theprint_bst(Node* root)function in the snippet:- Print the left subtree by calling
print_bst(root -> left)recursively. - Print the root by calling
printf("%d\n", root -> value). - Print the right subtree by calling
print_bst(root -> right)recursively.
If the tree has zero nodes (i.e., empty), we do nothing. If the tree has one node (i.e., root has no children):
If the tree has one node (i.e., root has no children):print_bst(root -> left)has no effect.printf("%d ", root -> value)prints 4 .print_bst(root -> right)has no effect.
 If the tree has three nodes (i.e., root has children but no grandchildren):
If the tree has three nodes (i.e., root has children but no grandchildren):print_bst(root -> left)prints 2 .printf("%d ", root -> value)prints 4 .print_bst(root -> right)prints 6 .
Altogether, it prints 2 4 6 . If the tree has seven nodes (i.e., root has children but no grandchildren):
If the tree has seven nodes (i.e., root has children but no grandchildren):print_bst(root -> left)prints 1 2 3 .printf("%d ", root -> value)prints 4 .print_bst(root -> right)prints 5 6 7 .
Altogether, it prints 1 2 3 4 5 6 7 .Fortree_sort_array(…), you are following the same process, except instead of printing a value withprintf(…), you store it in the array. - Print the left subtree by calling
Updates
| … | … |