Random Projections for High-dimensional Machine Learning
Analyzing data in high-dimensional spaces is a challenging problem due to the Curse of Dimensionality. The volume of the high-dimensional space increases at an exponential rate with increasing number of dimensions. This consequently leads to data samples becoming sparse in the high-dimensional space. Due to this, distance based metrics are not effective in distinguishing data samples based on classes or clusters. Further, the data analysis problem becomes untractable and computationally intensive for machine learning methods as the dimensionality increases. Dimension reduction techniques form an approach to this problem by attempting to reduce the dimensionality of the data in a manner that approximately preserves point distances in the original high-dimensional space. Following the reduction in dimensionality, the problem becomes more tractable and less computationally intensive for other machine learning methods. This approach is based on the Johnson-Lindenstrauss lemma. Some examples of these approaches include manifold learning methods and subspace clustering methods.
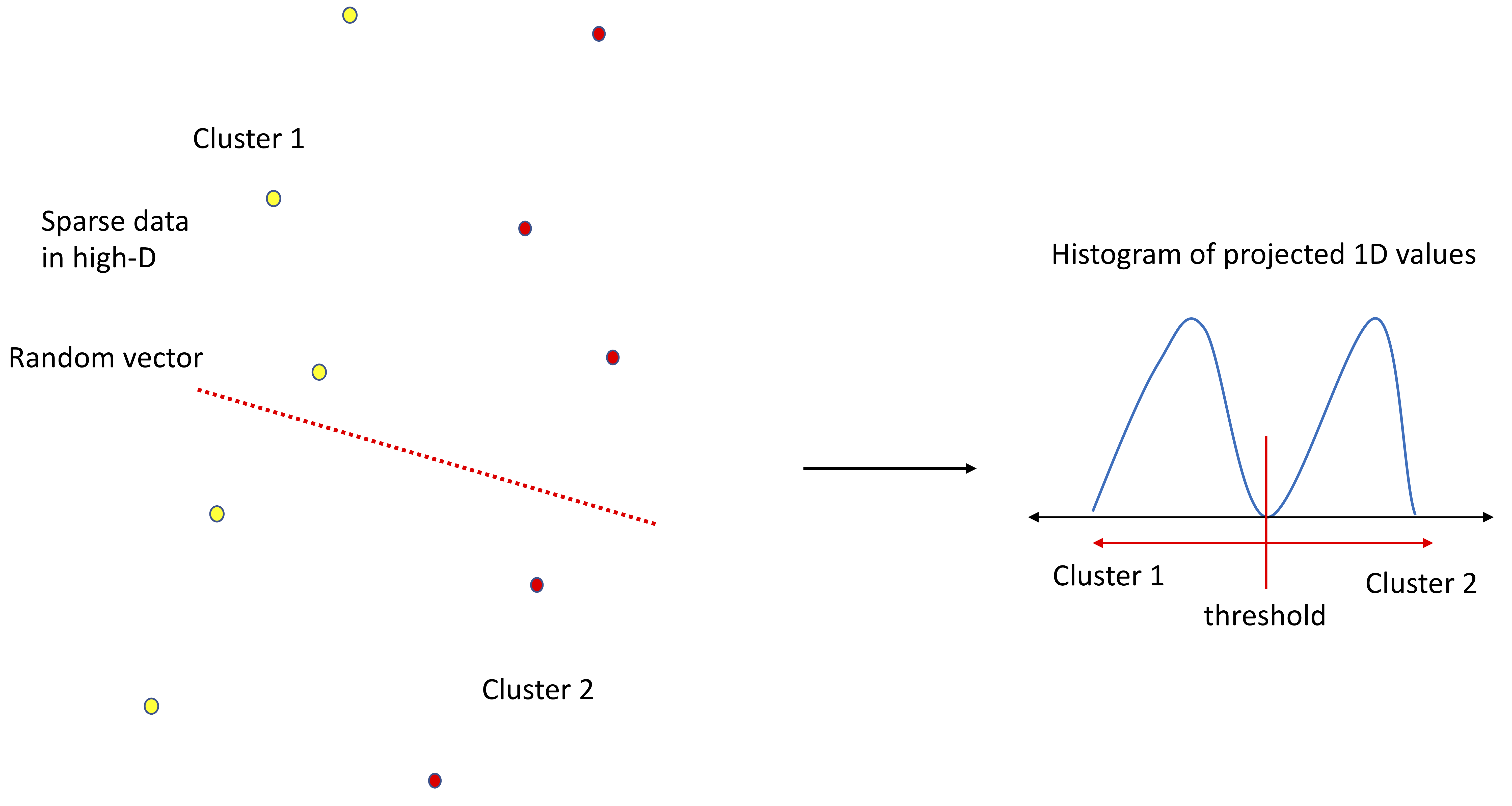
While most dimension reduction techniques transform data to a lower-dimensional space, the new dimensionality is greater than one. Further, this transformation is done in a point-proximity preserving manner so as to approximately preserve distances and allow the use of distance metrics in machine learning methods. The n -TARP method proposed in this project can be considered an extreme case of dimenion reduction techniques. TARP stands for Thresholding After Random Projection. This method consists of transforming data in high-dimensions into one-dimensional projected values through projection (inner product) with a randomly generated vector in the original high-dimensional space. Previous work has shown that there exists a lot of hidden structure in "real" high-dimensional data which can be exposed through simple random projections, which motivates the development and use of the n-TARP method. This random projection approach is repeated n times and the best separation resulting from the n attempts is chosen as the output of the n -TARP method. Best separation can be quantified through classification accuracy in the supervised scenario and optimal bi-modal separation in the unsupervised scenario. Clusters or Classes are assigned in this one-dimensional space of projected data, which is reflected back to the data samples in the original high-dimensional space. Note that the n -TARP method does not preserve distances and point-proximity structures. Instead it looks to expose point-separation structures in the one-dimensional space of projected data.
The n -TARP method can be considered as a basic building block that can be combined in different ways to form more complex methods in both supervised and unsupervised scenarios. One example of such a structure is a hierarchical tree structure built with n -TARP units at each node. The n -TARP method has been shown to perform favorably in comparison to other machine learning methods in both supervised and unsupervise scenarios. It has been used to formulate classification performance benchmarks in the supervised scenario and to analyze and cluster high-dimensional data in the unsupervised scenario. A statistical validation framework is combined with the n -TARP clustering approach to validate statistical significance of the formed clusters, which is a very challenging problem in high-dimensions due to the Curse of Dimensionality. Further, a pattern depedence framework based on the n -TARP method has been proposed as an alternative cluster validation tool and to identify the existence of a relationship between a given set of predictors and a response in a statistically valid manner. These tools have been combined to analyze data in an Educational Data analysis study to yield insightful results.