ECE264  Advanced C Programming

IPA 2-1: Decoding a Huffman Encoded File Header

Due November 13, 2012 @ 6:00 pm

 

The description is mainly taken from Professor Vijay Raghunathan. In this assignment, you will utilize your knowledge about priority queues, stacks, and trees to design a file compression program and file decompression program (similar to zip and unzip). You will base your utilities on the widely used algorithmic technique of Huffman coding, which is used in JPEG compression as well as in MP3 audio compression.

 

ASCII coding

 

Many programming languages use ASCII (which stands for American Standard Code for Information Interchange) coding to represent characters. In ASCII coding, every character is encoded (represented) with the same number of bits (8-bits) per character. Since there are 256 different values that can be represented with 8-bits, there are potentially 256 different characters in the ASCII character set, as shown in the ASCII character table available at http://www.asciitable.com/.

 

Let us now look at a simple example of ASCII encoding of characters. Using ASCII encoding (8 bits per character) the 13-character string "go go gophers" requires 13 * 8 = 104 bits. The table below shows how the coding works.

 

 

The given string would be written as the following stream of bits (the spaces would not be written, just the 0's and 1's)

 

01100111 01101111 00100000 01100111 01101111 00100000 01100111 01101111 01110000 01101000 01100101 01110010 01110011

 

From ASCII coding towards Huffman coding

 

Next, let us see how we might use fewer bits using a simpler coding scheme. Since there are only 8 different characters in "go go gophers", it is possible to use only 3-bits to encode the 8 different characters. We might, for example, use the coding shown in the table below (keep in mind that other 3-bit encodings are also possible).

 

 

Now the string "go go gophers" would be encoded as: 000 001 111 000 001 111 000 001 010 011 100 101 110. As you can see, by using three bits per character instead of eight bits per character that ASCII uses, the string "go go gophers" uses a total of 39 bits instead of 104 bits.

 

However, even in this improved coding scheme, we used the same number of bits to represent each character, irrespective of how often the character appears in our string. Even more bits can be saved if we use fewer than three bits to encode characters like g, o, and space that occur frequently and more than three bits to encode characters like e, h, p, r, and s that occur less frequently in "go go gophers". This is the basic idea behind Huffman coding: to use fewer bits for characters that occur more frequently. We'll see how this is done using a tree data structure that stores the characters as its leaf nodes, and whose root-to-leaf paths provide the bit sequence used to encode the characters.

 

Towards a Coding Tree

 

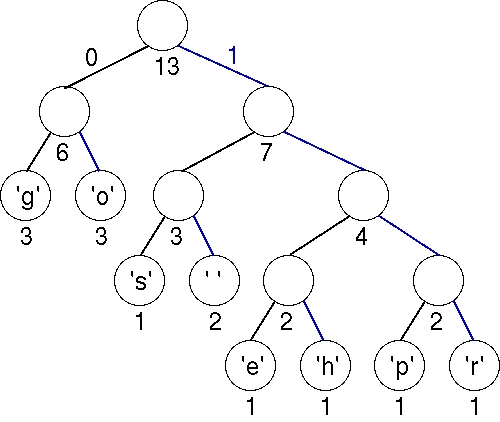
Using a binary tree for coding, all characters are stored at the leaves of a tree. A left-edge is numbered 0 and a right-edge is numbered 1. The code for any character/leaf node is obtained by following the root-to-leaf path and concatenating the 0's and 1's. The specific structure of the tree determines the coding of any leaf node using the 0/1 edge convention described. As an example, the tree below on the right yields the coding shown on the left.

 

 

Using this coding, "go go gophers" is encoded (again, spaces would not appear in the bit-stream) as: 00 01 101 00 01 101 00 01 1110 1101 1100 1111 100. This is a total of 37 bits, two bits fewer than the improved encoding in which each of the 8 characters has a 3-bit encoding! The bits are saved by coding frequently occurring characters like 'g' and 'o' with fewer bits (here two bits) than characters that occur less frequently like 'p', 'h', 'e', and 'r'.

 

To decode a given stream that has been coded by the given tree, start at the root of the tree, and follow a left-branch if the next bit in the stream is a 0, and a right branch if the next bit in the stream is a 1. When you reach a leaf, write the character stored at the leaf, and start again at the top of the tree. The bit stream 10011101101110011111100 yields right-left-left to the letter 's', followed (starting again at the root) with right-right-right-left to the letter 'p', followed by right-right-left-right to the letter 'h'. Continuing thus yields a decoded string "sphere."

 

Prefix codes

 

When all characters are stored in leaves, and every interior (non-leaf) node has two children, the coding induced by the 0/1 convention outlined above satisfies a very important property called the prefix property which states that no bit-sequence encoding of a character is the prefix of the bit-sequence encoding of any other character. This makes it possible to decode a bitstream using the coding tree by following root-to-leaf paths. The tree shown above for "go go gophers" satisfies this prefix property and is an optimal tree. There are other trees that use 37 bits; for example you can simply swap any sibling nodes and get a different encoding that uses the same number of bits. Next, we look at an algorithm for constructing such an optimal tree. This algorithm is called Huffman coding, and was invented by David A. Huffman in 1952 when he was a Ph.D. student at MIT.

 

 

Huffman Coding

In the previous section we saw examples of how a stream of bits can be generated from an encoding. We also saw how the tree can be used to decode a stream of bits. We'll discuss how to construct the tree here using Huffman's algorithm.

 

We'll assume that associated with each character is a weight that is equal to the number of times the character occurs in a file. For example, in the string "go go gophers", the characters 'g' and 'o' have weight 3, the space has weight 2, and the other characters have weight 1. When compressing a file we'll need to first read the file and calculate these weights. Assume that all the character weights have been calculated. Huffman's algorithm assumes that we're building a single tree from a group (or forest) of trees. Initially, all the trees have a single node containing a character and the character's weight. Iteratively, a new tree is formed by picking two trees and making a new tree whose child nodes are the roots of the two trees. The weight of the new tree is the sum of the weights of the two sub-trees. This decreases the number of trees by one in each iteration. The process iterates until there is only one tree left. The algorithm is as follows:

 

1. Begin with a forest of trees. All trees have just one node, with the weight of the tree equal to the weight of the character in the node. Characters that occur most frequently have the highest weights. Characters that occur least frequently have the smallest weights.
2. Repeat this step until there is only one tree:

    

   Choose two trees with the smallest weights; call these trees T₁ and T₂. Create a new tree whose root has a weight equal to the sum of the weights T₁ + T₂ and whose left sub-tree is T₁ and whose right sub-tree is T₂.

3. The single tree left after the previous step is an optimal encoding tree.

 

We shall use the string "go go gophers" as an example. Initially we have the forest shown below. The nodes are shown with a weight that represents the number of times the node's character occurs in the given input string/file.

 

 

We pick two minimal nodes. There are five nodes with the minimal weight of 1. In this implementation, we maintain a priority queue with items arranged according to their weights. When two items have the same weight, a leaf node (i.e., a node associated with an ASCII character) is always ordered first. If both nodes are leaf nodes, they are ordered according to their ASCII coding. If both nodes are non-leaf nodes, they are ordered according to the creation times of the nodes. We always pick the first two items in the priority queue, namely, nodes for characters 'e' and 'h'. We create a new tree whose root is weighted by the sum of the weights chosen. The order of the nodes in the priority queue also determines the left and right child nodes of the new root. We now have a forest of seven trees as shown here. Although the newly created node has the same weight as Space, it is ordered after Space in the priority queue because Space is an ASCII character.

 

 

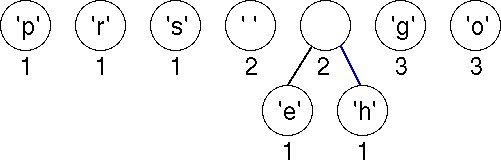
Choosing the first two (minimal) nodes in the priority queue yields another tree with weight 2 as shown below. There are now six trees in the forest of trees that will eventually build an encoding tree.

 

 

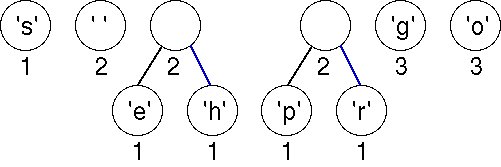
Again we must choose the first two (minimal) nodes in the priority queue. The lowest weight is the 'e'-node/tree with weight equal to 1. There are three trees with weight 2; the one chosen corresponds to an ASCII character because of the way we order the nodes in the priority queue. The new tree has a weight of 3, which will be placed last in the priority queue according to our ordering strategy.

 

 

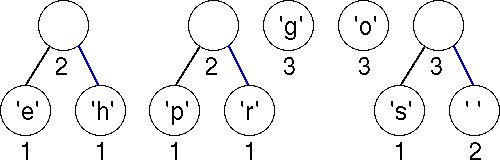
Now there are two trees with weight equal to 2. These are joined into a new tree whose weight is 4. There are four trees left, one whose weight is 4 and three with a weight of 3.

 

 

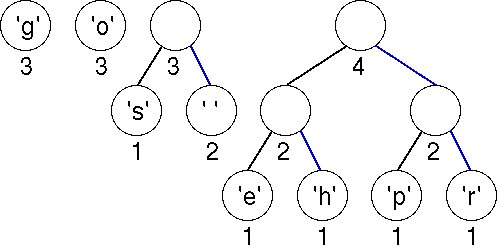
The first two minimal (weight 3) trees in the priority queue are joined into a tree whose weight is 6. There are three trees left.

 

 

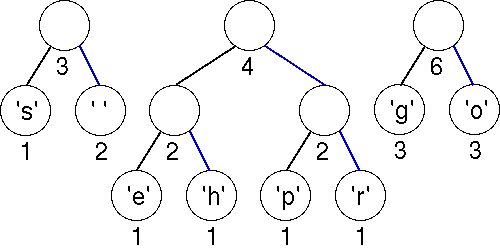
The minimal trees have weights of 3 and 4; these are joined into a tree with weight 7.

 

 

Finally, the last two trees are joined into a final tree whose weight is 13, the sum of the two weights 6 and 7. This tree is the tree we used to illustrate Huffman coding above. Note that you can easily come up with an alternative optimal tree by using a different ordering strategy to order trees of the same weights. In that case, the bit patterns for each character are different, but the total number of bits used to encode "go go gophers" is the same.

 

 

We now show another tree to compress the string "streets are stone stars are not" optimally. To encode "streets are" we would have the following bits: 1110001111011000111101010011110.

 

Another Huffman Tree/Table Example
Character Binary value '  ' 101 'a' 010 'e' 110 'n' 1000 'o' 1001 'r' 011 's' 111 't' 00

 

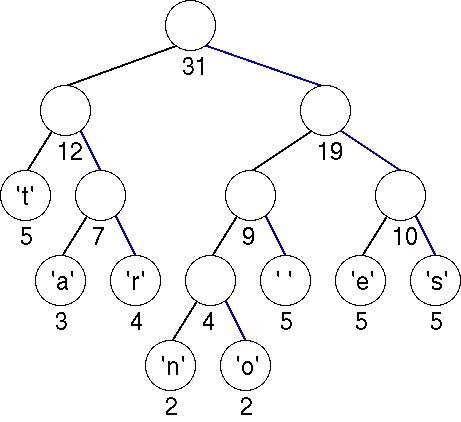
It is important to note that you cannot use the tree built for the string "go go gophers" to decode the bitstreams obtained from the encoding of "streets are stone stars are not" as the encoding is performed using a different tree.

 

Header Information

 

You must store some initial information in the compressed file that will be used by the decompression/unhuffing program. Basically, you must store the tree that is used to compress the original file. This is because the decompression program needs this exact same tree in order to decode the data. The header information contains:

• The topology of the Huffman coding tree. To store the tree at the beginning of the file, we use a post-order traversal, writing each node visited. When you encounter a leaf node, you write a 1 followed by the ASCII character of the leaf node. When you encounter a non-leaf node, you write a 0. To indicate the end of the Huffman coding tree, we write another 0.

• The total number of characters in the input file, followed by a newline character.

 

Consider the string "go go gophers", the header information is "1g1o01s1 01e1h01p1r0000013\n", where "\n" is the newline character. The post-order traversal of the Huffman coding tree gives us "1g1o01s1 01e1h01p1r0000". Another "0" separates the topology from "13", which is the number of characters in the input file.

 

For the string "streets are stone stars are not", the header information is "1t1a1r001n1o01 01e1s000031\n"..  The resulting tree would look like this

 

The numbers below each leaf node corresponds to itnumber of instance each characters appears in the file.  For this assignment, you do not need to worry about this.

 

In these two examples, we use characters 0 and 1 to distinguish between non-leaf and leaf nodes (and 0 to indicate the end of a topology). As there are eight leaf nodes in each of the two examples, there are eight 1's, seven 0's for non-leaf nodes, and another one 0 to indicate that we have reached the end of a topology. This approached used a total of 24 bytes.

 

To construct a Huffman coding tree from the header information, we make use of a stack. When a 1 is read, we read the corresponding ASCII character and push a node containg the character onto the stack. When a 0 is read, if the stack contains only one element, we have constructed the entire Huffman coding tree. Otherwise, there must be more than one element in the stack. We create a new node, and pop the top two elements off the stack. We make the first element off the stack the right child of the new node, and the second element off the stack the left child of the new node. After that, we push the newly created node onto the stack. 

 

IPA 2-1 (5 points)

 

In this assignment, you will write a program that takes in a compressed file and generates the Huffman tree specified by the header.

 

There will not be a skeleton provided for this assignment.  It will be up to you to define all functions.  Your program should have at least 2 .c files and 1 .h file.  You can click here for a .zip containg files that will be helpful in the testing of your algorithm  They include

• tree.h - a header file containing the function header  for the function PostOrderWalk as well as the the defintion of the LEAF structure. You must use this defintions for your tree nodes.  Do not edit the provided header file.  The function header for PostOrderWalk  is
  • void PostOrderWalk (LEAF* root)
• tree.o - an object file that contains the compiled version of PostOrdererWalk.  tree.o was compiled on a Linux machine in EE 206/207.  It will NOT work for Windows, MAC OS/ and other flavors of Linux/Unix.  Do not write your own version of PostOrderWalk.
• A suite of tescases and their solutions

You should use the function PostOrderWalk to check the structure of your tree to see if the tree was created properly.  We will be using this function to check the structure during grading.  The function take the root of your tree as the as a parameter.     

 

 

 

Sample Output

Consider the compressed file for string "streets are stone stars are not", the output file of the program should read as follows:

Requirements

• The program takes one input argument as the compressed file. If this input file name is not provided, the program prints an error message and terminates with return value EXIT_FAILURE. If the file cannot be opened, it also prints an error message and returns EXIT_FAILURE.  This constant is defined in stdlib.h and your program needs to include that header file.
• You must include a Makefile in your submission.  Your program will be compiled and built using your Makefile. The name of the executable file must be 'ipa2_1' (case-sensitive, no extension, not ipa2_1.exe).
• Your code needs to follow the coding standards specified here.  We will manually check this and you can lose points if standards are not followed.  You can find examples of how to follow the coding standards here.
• Your program will read the compressed file and keep track of all necessary information in memory.
• Your algorithm must meet the strategy requirements in the [Strategy] section. 

 

Hints

• You need to use structures for this assignment.  A structure about the Huffman coding should include the relevant information 
• We will check whether your program initializes all pointers to NULL.  This can be accomlished in the following ways
  • int * ptr = NULL; /* initialized to NULL, required */
  • int * ptr; 

• int * ptr = malloc(numberElement * sizeof(int));

If you write the following code without initialization, you will lose 0.2 point.

• int * ptr; /* uninitialized pointer. NOT ALLOWED */

 

Why do we check this? Uninitializing pointers make a program's behavior unpredictable.

(You are also allowed to declare and allocate memory for a pointer immediately using malloc() or calloc().)

I

 

WHAT YOU NEED TO SUBMIT?

 

1.     All the .c and .h files needed to execute your assignment.  All submission for this IPA should have at least 2 .c files and 1 .h file.  You can have more .c and .h files as you see fit.  Any submissions with one .c file will have points deducted.

2.    Makefile to compile your assignment.  For each submission, the executable  should be names ipa2_* where * is a number 1-2 depending on what part you are submitting.  For example, for IPA 2-3, the executable for that assignment should be ipa2_3.

3.   A README file that describes the algorithm used in your assignment.  The README should say how the functions accomplish their goals, not just the goals themselves. 

 

HOW TO SUBMIT?

 

1.    You can submit as many submission on the checking website as you would need.  For this assignment, if you pass the testcases on the server,  it will not guarantee a perfect score during grading.  

2.     Your submission for grading should be submitted through Blackboard.  You can submit as many times on Blackboard as you need before the deadline. We will grade the final submission, so please make sure that it is your FINAL version with everything included.  

 

HOW WILL WE GRADE YOUR SUBMISSION?

 

We will grade your assignments on algorithm correctness through DDD, memory allocation and deletions through valgrind , proper coding standards, content of README, a proper Makefile, and commenting.