ME 200 – Thermodynamics I – Spring 2020

Homework 3: Density, Pressure

Part (i): Divided Box

Part (ii): A Piston-Cylinder

Part (iii): Straw

Part (iv): Manometer

Part (i): Divided Box

Given:

A free-moving piston separates components into compartments A and B as shown below. The initial volumes of component A and component B are equal, and the total volume occupied by the two components is $1.0$ $m^3$. The initial specific volumes are $v_{A1}=100.0$ $m^3/kg$ and $v_{B1}=50.0$ $m^3/kg$. The piston is then moved so that x is one-fourth of the entire length (compartment A is one-fourth the total volume). The following code window defines this initial data for later computations.

In [34]:
#Given Inputs
Vol_A_1 = 0.5  # initial volume of compartment A [m^3]
Vol_B_1 = 0.5  # initial volume of compartment B [m^3]
v_A_1 = 100.0  # initial specific volume for compartment A [m^3/kg]
v_B_1 = 50.0   # initial specific volume for compartment B [m^3/kg]
Vol_A_2 = 0.25 # final volume of compartment A [m^3]
Vol_B_2 = 0.75 # final volume of compartment B [m^3]

Find:

The final specific volumes in chambers A and B.

System Sketch:

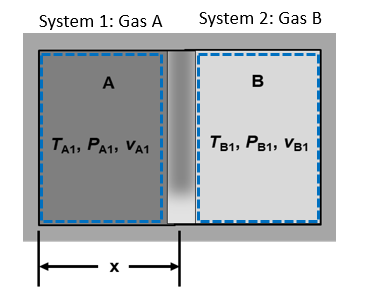
Basic Equations:

$$v=V/m$$

Solution:

First, the mass of the gas in each compartment is calculated with $m=V/v$ using the initial state. During the prcoess, the mass is constant for each compartment but the volume changes. Thus, the final specific volumes are calculated using the final volumes and original masses with $v=V/m$. The following code cell determines and prints the final specific volumes.

In [35]:
m_A = Vol_A_1/v_A_1 # mass of gas in compartment A, [kg]
m_B = Vol_B_1/v_B_1 # mass of gas in compartment B, [kg]
v_A_2 = Vol_A_2/m_A # final specific volume of gas in compartment A, [kg]
v_B_2 = Vol_B_2/m_B # final specific volume of gas in compartment B, [kg]

print('v_A_2 = ',round(v_A_2,5),'m^3/kg')
print('v_B_2 = ',round(v_B_2,5),'m^3/kg')

v_A_2 =  50.0 m^3/kg
v_B_2 =  75.0 m^3/kg

Part(ii): A Piston-Cylinder

Given:

A cylinder encloses a gas that is supporting a piston against atmospheric pressure and a mass as shown. The area of the piston is $0.01$ $m^2$, the atmospheric pressure is $0.101$ $MPa$ (abs), the local gravitational acceleration, $9.81$ $m/s^2$, and the supported mass is 50 kg.

In [36]:
# Assign Inputs

A_p = 0.01    # area of pistion [m^2] 
P_atm = 101   # atmospheric pressure [kN/m^2]
g = 9.81      # acceleration due to gravity [m/s^2]
m_p = 50      # piston mass [kg]

Find:

(a) the equilibrium gas pressure (kPa (abs)), and

(b) whether equilibrium gas pressure changes if gas volume doubles. Explain why or why not.

System Sketch:

Basic Equations:

$$\Sigma F=0, P = \dfrac{F}{A}$$

Solution:

(a) Equilibrium gas pressure (kPa)

A static force balance on the piston (see FBD above) results in

$$F_{gas}=F_{atm}+m_pg$$

where $F_{atm}$ is the force due to atmospheric pressure acting downward on the piston area ($A_pP_{atm}$) and $F_{gas}$ is the force due to the gas in the cylinder acting upward on the piston area ($A_pP_{atm}$). Then,

$$A_pP_{gas}=A_pP_{atm}+m_pg$$

and

$$P_{gas}=P_{atm}+\dfrac{m_pg}{A_p}$$
In [37]:
P_gas = P_atm + m_p*g/A_p/1000  # gas pressure [kPa]

print('Equilibrium gas pressure = ',round(P_gas,2),'kPa')

Equilibrium gas pressure =  150.05 kPa

(b) Does the equilibrium gas pressure change if the gas volume beneath the piston is doubled? Explain why or why not!

The equilibrium pressure is the same regardles of the volume because the static force balance is the same. For instance, if there were some heat transfer to the gas and the temperature rose, then the gas would expand and the piston would move upward until the gas pressure once again was balanced by the mass and atmospheric pressure. If the process occurs very slowly, then each state along the process can be considered to be in equilibrium. This is termed a "quasi-equilibrium" or "quasi-static" process. For this example, this would result in a constant pressure process.

Part (iii): Straw

Given:

Water suspended in a straw due to a difference in pressure above and below the column. The water column is 5 cm high and has a density of $1000$ $kg/m^3$. The atmospheric pressure is $101$ $kPa$ (abs). Neglect any surface tension effects.

In [38]:
#Given Inputs
rho_water = 1000   # water density[kg/m^3]
P_atm =101         # atmospheric pressure [kPa]
h = 0.05           # height of water column [m]

Find:

The pressure (kPa (abs)) of the air inside of the straw at the top of water column.

System Sketch:

Basic Equations:

$$\Delta P=\rho gh$$

Solution:

Considering a force balance on the water (see FBD above), the atmosphere below the water column must support the weight of the column and the force due to the pressure above the column such that

$$AP_{atm}= \rho_{water}g(hA)+AP_{straw}$$

Then, the pressure of the air above the column must satisfy

$$P_{straw}= P_{atm}-\rho_{water}gh$$

This is the same result realized by applying the basic equation: $\Delta P=\rho gh$ to the column.

In [39]:
g = 9.81 # acceleration due to gravity [m/s^2]
P_straw = P_atm-rho_water*g*h/1000

print('Straw Pressure= ',round(P_straw,2),'kPa')

Straw Pressure=  100.51 kPa

Part (iv): Manometer

Given:

The water in a tank is pressurized by air and the pressure is measured by a multi-fluid manometer as shown in the figure with the following data: $h_1 = 0.2$ $m$, $h_2 = 0.3$ $m$, and $h_3 = 0.46$ $m$. Densities for water, oil, and mercury are $1000$ $kg/m^3$, $850$ $kg/m^3$, and $13,600$ $kg/m^3$, respectively.

In [40]:
#Given Inputs
h_1 = 0.2 #[m]
h_2 = 0.3 #[m]
h_3 = 0.46 #[m]
rho_water = 1000 #[kg/m^3]
rho_oil = 850 #[kg/m^3]
rho_mercury = 13600 #[kg/m^3]

Find:

The gage pressure of air in the tank.

System Sketch:

Basic Equations:

$$\Delta P=\rho gh$$

Solution:

The pressure of the air in the tank is equal to the sum of the atmospheric pressure and the changes in pressure across each of the liquid columns from the atmosphere to the air in the tank or

$$P_{air}= P_{atm} + \Delta P_{mercury} + \Delta P_{oil} + \Delta P_{water}$$

where $\Delta P$ is positive going down a column and negative going up a column. Then, for each of the fluid columns

$$\Delta P_{mercury}=+\rho_{mercury}gh_3$$$$\Delta P_{oil}=-\rho_{oil}gh_2$$$$\Delta P_{water}=-\rho_{water}gh_1$$

Also, gage pressure is the difference between absolute and atmospheric pressure such that

$$P_{air,gage} = P_{air} - P_{atm} = \Delta P_{mercury} + \Delta P_{oil} + \Delta P_{water}$$
In [41]:
g = 9.81 # acceleration due to gravity [m/s^2]

DP_mercury = rho_mercury*g*h_3/1000  # pressure increase in mercury column from atmosphere [kPa]
DP_oil = -rho_oil*g*h_2/1000         # pressure decrease in oil column [kPa]
DP_water = -rho_water*g*h_1/1000     # pressure decrease in water column [kPa]

P_air_gage = DP_mercury + DP_oil + DP_water

print('Air Gage Pressure = ',round(P_air_gage,2),'kPa')

Air Gage Pressure =  56.91 kPa