ME 200 – Thermodynamics I – Spring 2020¶
Homework 26: Entropy Evaluations for Incompressible Substances¶
Part (i): Methods for Calculating Specific Internal Energy and Enthalpy Changes of Incompressibles¶
Part (ii): Copper cooling¶
Find:¶
Compare the changes in specific entropy for liquid water as determined using the following approaches:
a) Compressed liquid values
b) Saturated liquid values
c) Constant specific heat evaluated at the average temperature
d) Constant specific heat evaluated at the initial temperature
Basic Equations:¶
$$ds = c \dfrac{dT}{T} $$Assumptions:¶
1) constant specific heat
Solution:¶
The given pressure information can be used in checking whether the water is a liquid at the specified temperatures. Since the saturation temperature at 2500 kPa is 223.95°C for water, then water at both 20°C and 80°C is a compressed liquid.
Part a)¶
Since the pressure is 25 bar the compressed liquid tables can be used to determine the entropy at states 20°C and 80°C.
s_80 = 1.0740 # specific entropy of water @ 80°C and 25 bar [kJ/kg-K]
s_20 = 0.29596 # specific entropy of water @ 20°C and 25 bar [kJ/kg-K]
Delta_s_a = s_80 - s_20 # change in specific entropy [kJ/kg-K]
print('Delta_s_a = ',round(Delta_s_a,5),'(kJ/kg-K)')
Part b)¶
In the case of saturated liquid values, the change in entropy can be determined as a difference in two saturated liquid values at the two specific temperatures: $\Delta s = s_{f,80 °C} - s_{f,20°C}$
s_f_80 = 1.0756 # specific entropy of saturated water @ 80°C [kJ/kg-K]
s_f_20 = 0.296480 # specific entropy of saturated water @ 20°C [kJ/kg-K]
Delta_s_b = s_f_80 - s_f_20 # change in specific entropy [kJ/kg-K]
print('Delta_s_b = ',round(Delta_s_b,5),'(kJ/kg-K)')
Part c)¶
Using constant specific heats at $T = \bar T = 323.15 K$ requires linear interpolation between 300 and 325 K for the specific heat of water. The tables use the symbol $c_p$ for incompressible substances, but for an incompressible $c_p = c_v = c$ and so we'll use the symbol $c$. For a constant specific heat:
$$\Delta s=\int \dfrac{c}{T}dT = \bar c ln \big (\dfrac{T_2}{T_1}\big )$$import numpy as np
c_Tbar = 4.182 # specific heat at average temeprature of 323.15 K [kJ/(kg-K)]
T_2 = 80+273.15 # temperature at state 2 [K]
T_1 = 20+273.15 # temperature at state 1 [K]
delta_s_c = c_Tbar*np.log(T_2/T_1) # change in specific entropy with spec heat at average temp [kJ/kg-K]
print('delta_s_c = ',round(delta_s_c,5),'(kJ/kg-K)')
Part d)¶
Using constant specific heats at $T = T_i = 293.15 K$ requires interpolation between 275 K and 300 K. The same equation as in part (c) is used.
c_Ti = 4.188 # specific heat at T = T_i = 293.15 K [kJ/(kg-K)]
delta_s_d = c_Ti*np.log(T_2/T_1) # change in specific entropy with spec heat at average temp [kJ/kg-K]
print('delta_s_d = ',round(delta_s_d,5),'(kJ/kg-K)')
The four approaches give almost the same results!
# Given Inputs
m_Cu = 2 # mass of copper [kg]
T_1 = 50 # initial copper temperature [°C]
T_surr = 10 # temperature of surroundings [°C]
T_2 = T_surr # final copper temperature [°C]
Find:¶
a) Heat transfer for the copper in kJ
b) Change in entropy of the copper in kJ/k
c) Change in entropy of the surrounding in kJ/K
System Diagram:¶
Choose the copper as the system for parts a and b. The surroundings is the system for part c.
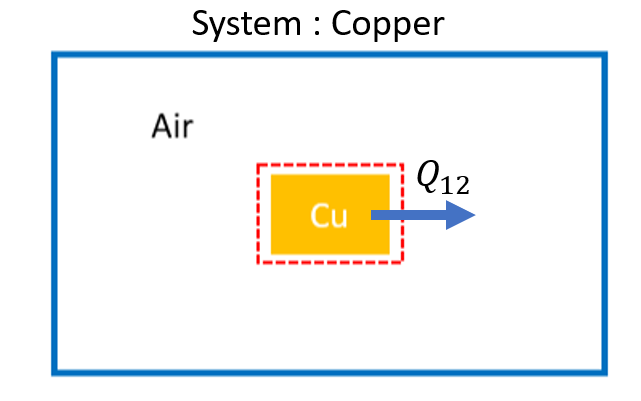
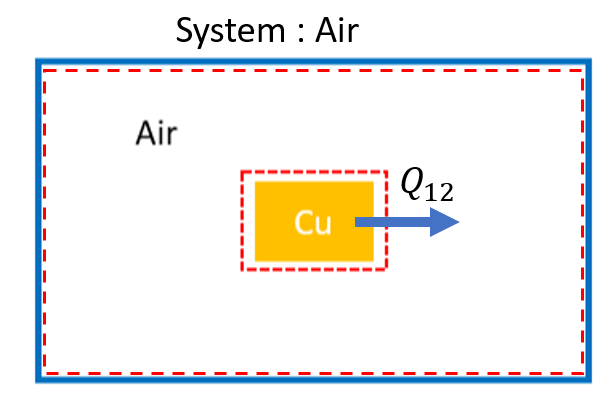
Basic Equations:¶
$$\dfrac{dE}{dt} = \dot Q- \dot W + \displaystyle\sum_{in} \dot m_{in} (h+ke+pe)_{in}-\displaystyle\sum_{out} \dot m_{out}(h+ke+pe)_{out}$$$$du = cdT, ds = c \dfrac{dT}{T}$$$$S_2 - S_1 = \int _1 ^2 \bigg (\dfrac{\delta Q}{T} \bigg )_{int,rev}$$Assumptions:¶
1) closed system, 2) room is at a constant and unform temperature, acting as a heat sink (internally reversible), 3) stationary (no changes in kinetic and potential energy) 4) copper treated as an incompressible substance, 5) constant specific heat for copper, 6) uniform temperature for copper at each state along the processes
Solution:¶
Part a)¶
The integrated form of the first law reduces to
$$\Delta E = \Delta KE + \Delta PE + \Delta U = Q - W \rightarrow Q = m\Delta u$$where $\Delta u$ is the change in internal energy of the copper during the process. For an incompressible with constant specific heat,
$$\Delta u = \int_{T_{1}}^{T_{2}} c dT = c(T_2-T_1)$$where the specific heat of copper is taken from the tables as
$$c_{Cu} = 0.385 \frac{kJ}{kg-K}$$Note that although the tables use the symbol $c_p$ for incompressible substances, there is only one specific heat for an incompressible ($c_p = c_v = c$) and so we use the symbol $c$.
The copper cools from its initial temperature of 50°C to the room temperature of 10°C. As a result, the heat transfer should be negative. The result of the following code confirms this intuition.
c_Cu = 0.385 # specific heat of copper [kJ/(kg-K)]
Q_12 = m_Cu*c_Cu*(T_2 - T_1) # heat Transfer [kJ]
print('Q_12 = ',round(Q_12,3),'kJ')
Part b)¶
In order to solve for the change in entropy for the copper block, the property relation for entropy change of an incompressible is employed with the constant specific heat from (a) and the intial and final temperatures of the block
$$\Delta s_{12}=\int_{T_{1}}^{T_{2}} c \dfrac{dT}{T} = c \cdot ln \big (\dfrac{T_2}{T_1}\big )$$$$\Delta S_{12}=m \cdot c \cdot ln \big (\dfrac{T_2}{T_1}\big )$$DeltaS_12_Cu = m_Cu*c_Cu*np.log((T_2+273.15)/(T_1+273.15)) # change in entropy [kJ/K]
print('DeltaS_12_Cu = ',round(DeltaS_12_Cu,3),'kJ/K')
Part c)¶
The heat transfer within the surroundings is assumed to be internally reversible. This implies that the temperature gradient between the copper and surroundings occurs over an infinitessimally small boundary layer between the copper and the surrounding air. Also, any heat transfer from the copper block is absorbed by the environment but has the opposite sign. Thus, treating the surroundings as an internally reversible heat transfer process at constant temperature, then
$$\Delta S_{surr} = \int _1 ^2 \bigg (\dfrac{\delta Q_{surr}}{T} \bigg )_{int,rev}=\dfrac{Q_{surr}}{T_{surr}}$$$$\Delta S_{surr}=-\dfrac{Q_{12}}{T_{surr}}$$DeltaS_surr = -Q_12/(T_surr+273.15) # change in entropy [kJ/K]
print('DeltaS_surr = ',round(DeltaS_surr,3),'kJ/K')