Fig 1: The geometry and coordinate system of the lid driven cavities.

Fig 2: isosurface of λ2 colored by V velocity magnitude at Re = 12,000 (80^3 grid; D3Q27 lattice model; Smagorinsky SGS model).
Based on the validation study in the cubic cavity, we apply the BGK-LBE with Smagorinsky model and D3Q27 lattice model on a 80^3 grid to the study the steady-oscillatory transition of the flows in lid driven cavities. For cubic cavity, oscillatory instabilities sets in via symmetry breaking about z=h plane at Re=2,250-2,300. The symmetry is recovered at Re=2,350, at which non-decaying oscillations exist in the flow field. For deep cavities with K=2, symmetry breaking is observed at Re=1,350-1,550, at which the flow first shows decaying oscillations and periodic oscillations occurs afer the flow is developed for a certain time.

Fig 3: Instantaneous velocity U, V, W contours on X-plane and stremlines on Z-plane at t0; Oscillations mainly occur on the Z-plane.
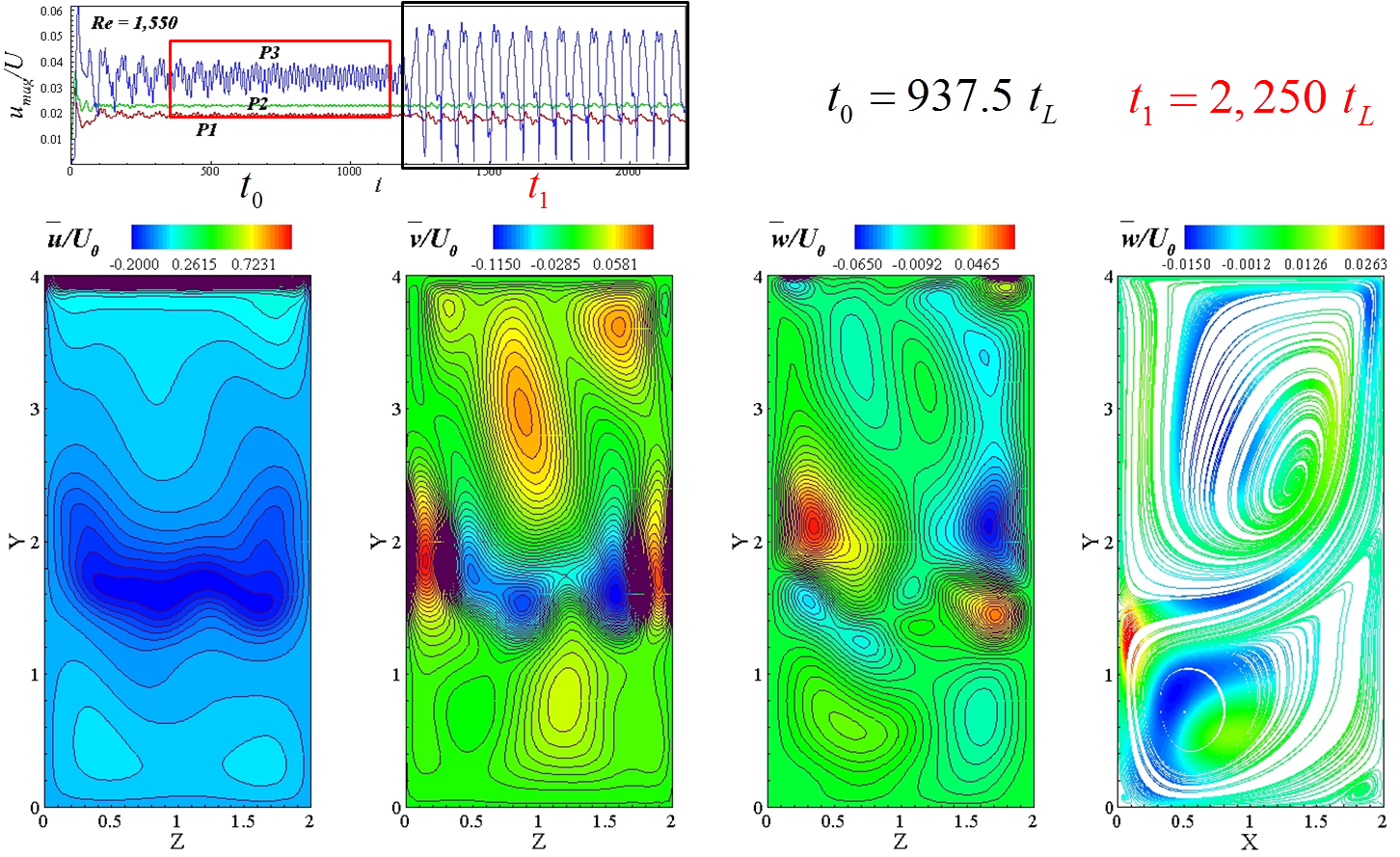
Fig 3: Instantaneous velocity U, V, W contours on X-plane and stremlines on Z-plane at t1; Oscillations transit to X-plane.
Prof. Frankel's MAIN PAGE